L4 Logistic Regression

最优分类器

贝叶斯最优分类器

分类器

\[y \leftarrow \underset{y \in \mathcal{Y}}{\operatorname{argmax}} \operatorname{Pr}[y|x] \]

在所有可能的分类器中是最优的。

• \(\operatorname{Pr}[y|x]\) 被称为 \(y\) 的后验概率。
• 含义：计算 \(\operatorname{Pr}[y|x]\) 以实现最优分类。
• 我们如何知道 \(\operatorname{Pr}[y|x]\)？
• 假设我们有训练数据
  \[\{(x_1, y_1), \dots, (x_n, y_n)\} \]

• 我们可以基于训练数据学习一个估计器 \(\operatorname{Pr}_{\theta}[y|x]\) 来估计 \(\operatorname{Pr}[y|x]\)。

逻辑函数 / S形函数

该函数被称为逻辑函数(logistic)或S形函数。(sigmoid)

\[h(t) = \frac{e^t}{e^t+1} = \frac{1}{1+e^{-t}} \]

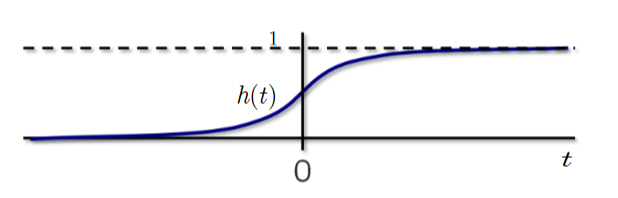
图像显示了逻辑函数的图形，呈现出'S'形状。x轴标记为't'，y轴标记为'h(t)'。图形在t的较大负值附近接近0，通过点(0, 0.5)增加，并在t的较大正值附近接近1。y=1的虚线表示渐近线。

二分类的逻辑回归模型

逻辑回归（LR）具有以下 \(Pr_{\theta}[y|x]\) 用于建模 \(Pr[y|x]\)：

\[Pr_{\theta}[y = +1|x] = h(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}} \]

\[Pr_{\theta}[y = -1|x] = 1 - Pr_{\theta}[y = +1|x] = \frac{1}{1 + e^{\theta^T x}} \]

因此，

\[Pr_{\theta}[y|x] = \frac{1}{1 + \exp(-y \cdot \theta^T x)} \]

• 学习过程是学习一个 \(\hat{\theta}\)，使得 \(Pr_{\hat{\theta}}[y|x]\) 能够很好地逼近潜在的 \(Pr[y|x]\)（至少在训练数据上）。
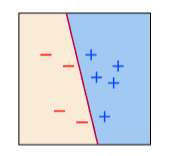
• 逻辑回归实际上是一种分类技术。
• 从本质上讲，它是为二分类量身定制的，\(y \in \{+1, -1\}\)。

假设我们已经学习了 \(\theta\)

\[Pr_{\theta}[y = +1|x] = \frac{1}{1 + e^{-\theta^T x}} > \frac{1}{2} （将 x 分类为类 +1） \]

这等价于 \(e^{-\theta^T x} < 1\)

这进一步等价于 \(\theta^T x > 0\)

因此

\[y = \begin{cases} +1, & \theta^T x > 0 \\ -1, & \theta^T x < 0 \end{cases} \]

逻辑回归：学习问题

• 所有数据 \(\{(x_i, y_i)\}\) 的似然（独立同分布）：

  \[\prod_{i=1}^{n} \text{Pr}_{\theta}[y_i | x_i] \]

• 回忆训练数据对：\(\{ (x_1, y_1), \dots, (x_n, y_n) \}\) 表示对于 \((x_i, y_i)\) 的后验概率

\[Pr_{\theta}[y_i | x_i] = \frac{1}{1 + \exp(-y_i \cdot \theta^T x_i)} \]

• 观察：给定参数 \(\theta\) 的 \((x_i, y_i)\) 的似然性。
  如何学习参数 \(\theta\)？
  最大似然估计原则。

• 所有数据 \(\{(x_i, y_i)\}\) 的对数似然：

  \[\sum_{i=1}^{n} \log(\text{Pr}_{\theta}[y_i | x_i]) = - \sum_{i=1}^{n} \log(1 + \exp(-y_i \cdot \theta^T x_i)) \]

• 最大似然估计导致学习问题：

  \[\hat{\theta} = \underset{\theta \in \mathbb{R}^d}{\operatorname{argmin}} \frac{1}{n} \sum_{i=1}^{n} \log(1 + \exp(-y_i \cdot \theta^T x_i)) \]

我们要最小化什么？通过逻辑损失测量的训练误差，有时也称为交叉熵损失。还与最小化样本内误差 \(Err_{in}\) 相关，使用 0-1 误差度量。

重新审视泛化：如何使 Er_out 变小

• 泛化理论说：

  \[\forall f_\theta \in \mathcal{H}, E_{out}(f_\theta) \leq E_{in}(f_\theta) + O(\sqrt{\frac{d_{VC}}{n}}) \]

• 目标：使 \(E_{out}\) 变小。

• 当 \(\mathcal{H}\) 和训练数据固定时，泛化误差是固定的。

• 通过选择特定的 \(f_\theta \in \mathcal{H}\) 来使 \(E_{in}(f_\theta)\) 变小。

如何做到？设计训练算法以选择一个 \(\hat{\theta}\) 使得：

\[\min_{\theta \in \mathbb{R}^d} E_{in}(f_\theta) \leftarrow \hat{\theta} = \underset{\theta \in \mathbb{R}^d}{\operatorname{argmin}} \sum_{i=1}^n \ell(f_\theta(x_i), y_i) \]

学习到的模型：\(f_{\hat{\theta}} \in \mathcal{H}\)，提供小的 \(E_{out}(f_{\hat{\theta}})\)。为制定逻辑回归问题提供了动机。

逻辑回归与最小二乘法

• 逻辑回归：逻辑损失

  \[\hat{\theta} = \underset{\theta \in \mathbb{R}^d}{\operatorname{argmin}} \frac{1}{n} \sum_{i=1}^n \log(1 + \exp(-y_i \cdot \theta^T x_i)) \]

• 最小二乘法：平方 \(l_2\)-范数损失

  \[\hat{\theta} = \underset{\theta \in \mathbb{R}^d}{\operatorname{argmin}} \|X\theta - y\|_2^2 \]

优化

• 最小二乘法：闭式解。
• 逻辑回归：无闭式解。

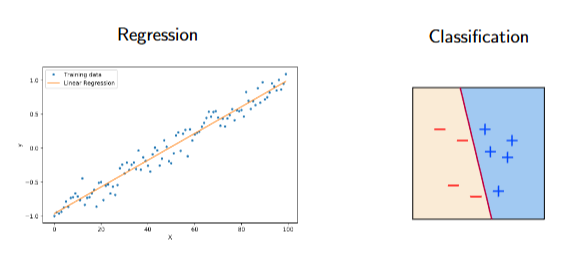
回归与分类

• 最小二乘法：专为回归设计。回归是拟合一个连续的量，\(y \in \mathbb{R}\) 是连续的。
• 逻辑回归：专为分类设计。分类是拟合离散标签，\(y \in \{-1,+1\}\) 是分类的。

多类逻辑回归

Softmax：逻辑函数的扩展

• 到目前为止，开发的逻辑回归是用于二分类的。 当类别数量 \(K > 2\) 时怎么办？

• 关键思想是为每个类别 \(k = 1, \dots, K\) 分配一个参数/权重向量 \(\theta_k\)。

• 设 \(\Theta = [\theta_1, \dots, \theta_K] \in \mathbb{R}^{(d+1) \times K}\)，并且 \(\{(x_i, y_i)\}_{i=1}^n\) 是训练数据。

• 用于估计 \(y_i\) 的后验概率的模型为

\[P(y_i = k | x_i) = \frac{\exp(\theta_k^T x_i)}{\sum_{j=1}^K \exp(\theta_j^T x_i)} \]

这也被称为 softmax。显然，\(Pr[y_i = k | \Theta, x_i]\) 对 \(k\) 的总和为 1。

多类逻辑回归

利用最大似然估计（MLE）的推理，我们可以将学习问题表述为

\[\hat{\Theta} = \underset{\Theta \in \mathbb{R}^{d \times K}}{\operatorname{argmin}} -\frac{1}{n} \sum_{i=1}^{n} \sum_{k=1}^{K} \mathbf{1}_{\{y_i=k\}} \log \left(\frac{\exp(\theta_k^T x_i)}{\sum_{j=1}^{K} \exp(\theta_j^T x_i)}\right) \]

其中 \(\mathbf{1}_{\{y_i=k\}}\) 是定义为

\[\mathbf{1}_{\{y_i=k\}} = \begin{cases} 1, & y_i \text{ 是 } k\text{-类} \\ 0, & \text{否则} \end{cases} \]

1. 二类逻辑回归的梯度

对于二类逻辑回归，目标函数为：

\[f(\theta) = -\frac{1}{n} \sum_{i=1}^n \left[ y_i \log(\sigma(\theta^T x_i)) + (1 - y_i) \log(1 - \sigma(\theta^T x_i)) \right] \]

\[\mathcal{L}(\theta) := \frac{1}{n} \sum_{i=1}^{n} \log(1 + \exp(-y_i \cdot \theta^T x_i)) \]

其中，(\sigma(z) = \frac{1}{1 + \exp(-z)}) 是 sigmoid 函数。

梯度为：

\[\frac{\partial f(\theta)}{\partial \theta} = \frac{1}{n} \sum_{i=1}^n x_i \cdot (\sigma(\theta^T x_i) - y_i) \]

---

2. 多类逻辑回归的梯度

对于多类逻辑回归，目标函数为：

\[f(\Theta) = -\frac{1}{n} \sum_{i=1}^n \sum_{k=1}^K \mathbf{1}_{\{y_i = k\}} \log \left( \frac{\exp(\theta_k^T x_i)}{\sum_{j=1}^K \exp(\theta_j^T x_i)} \right) \]

其中，(\Theta = [\theta_1, \theta_2, \dots, \theta_K] \in \mathbb{R}^{d \times K}) 是参数矩阵。

对于每个类别 (k)，梯度为：

\[\frac{\partial f(\Theta)}{\partial \theta_k} = \frac{1}{n} \sum_{i=1}^n x_i \cdot \left( \mathbf{1}_{\{y_i = k\}} - \frac{\exp(\theta_k^T x_i)}{\sum_{j=1}^K \exp(\theta_j^T x_i)} \right) \]

要清楚地理解 最大似然估计 (MLE)、损失函数、目标函数 和 梯度 之间的关系，我们可以从逻辑回归的背景出发，逐步分析它们的定义和联系。

---

1. 最大似然估计 (MLE)

最大似然估计是一种统计方法，用于估计模型参数，使得在给定数据下，模型生成数据的概率最大化。

在逻辑回归中的 MLE：

• 假设数据集为 ({(x_i, y_i)}_{i=1}^n)，其中 (x_i \in \mathbb{R}^d) 是特征向量，(y_i \in {1, 2, \dots, K}) 是类别标签。

• 我们希望找到参数 (\Theta = [\theta_1, \theta_2, \dots, \theta_K] \in \mathbb{R}^{d \times K})，使得模型对所有样本的联合概率 (\mathcal{L}(\Theta)) 最大化：

  \[\mathcal{L}(\Theta) = \prod_{i=1}^n \Pr(y_i | x_i; \Theta) \]

• 由于 (\Pr(y_i | x_i; \Theta)) 是通过 softmax 函数建模的：

  \[\Pr(y_i = k | x_i; \Theta) = \frac{\exp(\theta_k^T x_i)}{\sum_{j=1}^K \exp(\theta_j^T x_i)} \]

  联合概率可以写为：

  \[\mathcal{L}(\Theta) = \prod_{i=1}^n \frac{\exp(\theta_{y_i}^T x_i)}{\sum_{j=1}^K \exp(\theta_j^T x_i)} \]

对数似然函数：

为了简化计算，取对数得到对数似然函数：

\[\ell(\Theta) = \sum_{i=1}^n \log \Pr(y_i | x_i; \Theta) = \sum_{i=1}^n \left[ \theta_{y_i}^T x_i - \log \left( \sum_{j=1}^K \exp(\theta_j^T x_i) \right) \right] \]

MLE 与目标函数的关系：

• MLE 的目标： 最大化对数似然函数 (\ell(\Theta))。

• 目标函数： 为了方便优化，我们通常最小化负对数似然函数：

  \[f(\Theta) = -\frac{1}{n} \sum_{i=1}^n \left[ \theta_{y_i}^T x_i - \log \left( \sum_{j=1}^K \exp(\theta_j^T x_i) \right) \right] \]

---

2. 损失函数

损失函数是目标函数的核心部分，用于衡量模型预测值与真实值之间的差距。

单个样本的损失函数：

对于单个样本 ((x_i, y_i))，损失函数为：

\[\ell(\Theta; x_i, y_i) = - \left[ \theta_{y_i}^T x_i - \log \left( \sum_{j=1}^K \exp(\theta_j^T x_i) \right) \right] \]

目标函数与损失函数的关系：

目标函数是所有样本损失函数的平均值：

\[f(\Theta) = \frac{1}{n} \sum_{i=1}^n \ell(\Theta; x_i, y_i) \]

---

3. 梯度

梯度是目标函数对参数的导数，用于描述目标函数在参数空间中的变化率，指导优化算法更新参数。

梯度的计算：

目标函数对参数 (\theta_k) 的梯度为：

\[\frac{\partial f(\Theta)}{\partial \theta_k} = \frac{1}{n} \sum_{i=1}^n x_i \cdot \left( \mathbf{1}_{\{y_i = k\}} - \frac{\exp(\theta_k^T x_i)}{\sum_{j=1}^K \exp(\theta_j^T x_i)} \right) \]

梯度与目标函数的关系：

• 梯度是目标函数的导数，表示目标函数在参数空间中的变化方向。

• 梯度用于优化算法（如梯度下降）更新参数：

  \[\Theta \leftarrow \Theta - \eta \cdot \nabla f(\Theta) \]

  其中，(\eta) 是学习率，(\nabla f(\Theta)) 是目标函数的梯度。

---

4. 总结：MLE、损失函数、目标函数和梯度的关系

1. MLE 是理论基础，它告诉我们如何定义目标函数。
2. 损失函数 是目标函数的组成部分，衡量单个样本的误差。
3. 目标函数 是所有样本损失的平均值，用于衡量模型整体的误差。
4. 梯度 是目标函数的导数，用于优化算法更新参数，从而最小化目标函数。

---