分治策略(2)——算法导论(4)
1. 引言
这一篇博文主要介绍基于分治策略的矩阵乘法的Strassen算法。
2. 矩阵乘法的Strassen算法
矩阵乘法的基本算法的计算规则是:
若A=(aij)和B=(bij)是n×n的方阵(i,j = 1,2,3...),则C = A · B中的元素Cij为:
下面给出Java实现代码:
public static void main(String[] args) { int[][] a = new int[][] { // { 1, 0, 1, 2 }, // { 1, 2, 0, 2 }, // { 0, 2, 1, 0 }, // { 0, 0, 1, 2 },// }; int[][] b = new int[][] { // { 1, 0, 1, 2 }, // { 1, 2, 0, 2 }, // { 0, 2, 1, 0 }, // { 0, 0, 1, 2 },// }; printMatrix(squareMatrixMutiply(a, b)); } /** * 基本矩阵乘法(假定矩阵a和矩阵b都是n×n的矩阵,且n为2的幂) * @param a 矩阵a * @param b 矩阵b * @return */ private static int[][] squareMatrixMutiply(int[][] a, int[][] b) { int[][] c = new int[a.length][a.length]; for (int i = 0; i < c.length; i++) { for (int j = 0; j < c.length; j++) { c[i][j] = 0; for (int k = 0; k < c.length; k++) { c[i][j] += a[i][k] * b[k][j]; } } } return c; } /** * 打印矩阵 * * @param matrix */ private static void printMatrix(int[][] matrix) { for (int[] is : matrix) { for (int i : is) { System.out.print(i + "\t"); } System.out.println(); } }
为简单起见,当使用分治法(Divide and Conquer)计算矩阵C=A*B时,假定三个矩阵都是n×n的矩阵,并且n为2的幂。分治法(Divide and Conquer)还是上一篇提到的三个步骤,算法的核心就是这个公式:
其中,Aij,Bij,Cij分别是A,B,C矩阵的n / 2 * n / 2的子矩阵,即:
值得说明的是,我们不必创建子数组,那将浪费θ(n²)的时间来复制数组元素;明智的做法是直接根据下标运算。
下图是原书的伪代码(其中所说的“(4.9)”即为上图所给的三个等式):
下面给出Java实现代码:
public static void main(String[] args) { int[][] a = new int[][] { // { 1, 0, 1, 2 }, // { 1, 2, 0, 2 }, // { 0, 2, 1, 0 }, // { 0, 0, 1, 2 },// }; int[][] b = new int[][] { // { 1, 0, 1, 2 }, // { 1, 2, 0, 2 }, // { 0, 2, 1, 0 }, // { 0, 0, 1, 2 },// }; printMatrix(squareMatrixMutiplyByRecursive(new ChildMatrix(a, 0, 0, a.length), new ChildMatrix(b, 0, 0, b.length), 0, 0, 0, 0)); } /** * 打印矩阵 * * @param matrix */ private static void printMatrix(int[][] matrix) { for (int[] is : matrix) { for (int i : is) { System.out.print(i + "\t"); } System.out.println(); } } /** * 基于分治法的矩阵乘法 * * @param a * @param b * @return */ private static int[][] squareMatrixMutiplyByRecursive(ChildMatrix matrixA, ChildMatrix matrixB, int lastStartRowA, int lastStartColumnA, int lastStartRowB, int lastStartColumnB) { int[][] c = new int[matrixA.length][matrixA.length]; if (matrixA.length == 1) { c[0][0] = matrixA.getFromParentMatrix(matrixA.startRow, matrixA.startColumn) * // matrixB.getFromParentMatrix(matrixB.startRow, matrixB.startColumn); return c; } int childLength = matrixA.length / 2; // 第一步:分解 ChildMatrix childMatrixA11 = new ChildMatrix(matrixA.parentMatrix, lastStartRowA, lastStartColumnA, childLength); ChildMatrix childMatrixA12 = new ChildMatrix(matrixA.parentMatrix, lastStartRowA, lastStartColumnA + childLength, childLength); ChildMatrix childMatrixA21 = new ChildMatrix(matrixA.parentMatrix, lastStartRowA + childLength, lastStartColumnA, childLength); ChildMatrix childMatrixA22 = new ChildMatrix(matrixA.parentMatrix, lastStartRowA + childLength, lastStartColumnA + childLength, childLength); ChildMatrix childMatrixB11 = new ChildMatrix(matrixB.parentMatrix, lastStartRowB, lastStartColumnB, childLength); ChildMatrix childMatrixB12 = new ChildMatrix(matrixB.parentMatrix, lastStartRowB, lastStartColumnB + childLength, childLength); ChildMatrix childMatrixB21 = new ChildMatrix(matrixB.parentMatrix, lastStartRowB + childLength, lastStartColumnB, childLength); ChildMatrix childMatrixB22 = new ChildMatrix(matrixB.parentMatrix, lastStartRowB + childLength, lastStartColumnB + childLength, childLength); // 第二步:解决 int[][] temp1 = squareMatrixMutiplyByRecursive(childMatrixA11, childMatrixB11, 0, 0, 0, 0); int[][] temp2 = squareMatrixMutiplyByRecursive(childMatrixA12, childMatrixB21, 0, childLength, childLength, 0); int[][] c11 = sumMatrix(temp1, temp2); int[][] temp3 = squareMatrixMutiplyByRecursive(childMatrixA11, childMatrixB12, 0, 0, 0, childLength); int[][] temp4 = squareMatrixMutiplyByRecursive(childMatrixA12, childMatrixB22, 0, childLength, childLength, childLength); int[][] c12 = sumMatrix(temp3, temp4); int[][] temp5 = squareMatrixMutiplyByRecursive(childMatrixA21, childMatrixB11, childLength, 0, 0, 0); int[][] temp6 = squareMatrixMutiplyByRecursive(childMatrixA22, childMatrixB21, childLength, childLength, childLength, 0); int[][] c21 = sumMatrix(temp5, temp6); int[][] temp7 = squareMatrixMutiplyByRecursive(childMatrixA21, childMatrixB12, childLength, 0, 0, childLength); int[][] temp8 = squareMatrixMutiplyByRecursive(childMatrixA22, childMatrixB22, childLength, childLength, childLength, childLength); int[][] c22 = sumMatrix(temp7, temp8); // 第三步:合并 for (int i = 0; i < c.length; i++) { for (int j = 0; j < c.length; j++) { if (i < childLength && j < childLength) { c[i][j] = c11[i][j]; } else if (i < childLength && j < c.length) { int[][] child = c12; c[i][j] = child[i][j - childLength]; } else if (i < c.length && j < childLength) { int[][] child = c21; c[i][j] = child[i - childLength][j]; } else { int[][] child = c22; c[i][j] = child[i - childLength][j - childLength]; } } } return c; } private static int[][] sumMatrix(int[][] a, int[][] b) { int[][] c = new int[a.length][b.length]; for (int i = 0; i < a.length; i++) { for (int j = 0; j < a.length; j++) { c[i][j] += a[i][j]; c[i][j] += b[i][j]; } } return c; } /** * ChildMatrix 表示某个矩阵的一个子矩阵 * * @author D.K * */ static class ChildMatrix { /** * 父矩阵 */ int[][] parentMatrix; /** * 子矩阵在父矩阵中的起始行坐标 */ int startRow; /** * 子矩阵在父矩阵中的起始列坐标 */ int startColumn; /** * 子矩阵长度 */ int length; public ChildMatrix(int[][] parentMatrix, int startRow, int startColumn, int length) { super(); this.parentMatrix = parentMatrix; this.startRow = startRow; this.startColumn = startColumn; this.length = length; } /** * 获取父矩阵的row行,colum列元素 * * @param row * @param colum * @return */ public int getFromParentMatrix(int row, int colum) { return parentMatrix[row][colum]; } }
Strassen算法的核心思想是令递归树稍微不那么茂盛,它只进行7次递归(上面的分治法地递归了8次)。Strassen算法的描述如下:
① 分解矩阵A,B,C为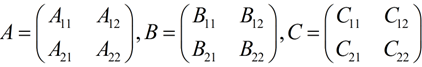
同样不要创建子数组而只是进行下标计算。
② 创建10个n/2 ×n/2的矩阵S1,S2,S3…,S10,其计算公式如下:
③ 递归地计算7个矩阵积P1, P2…P3,P7,计算公式如下:
④ 计算Cij,计算公式如下:
3. 算法分析
对于普通的矩阵乘法,3次嵌套循环,每层执行n次,所需时间为θ(n³);
① 基本情况:T(1) = θ(1);
② 递归情况:分解后,矩阵规模变为原来的1/2。递归八次,用时8T(n/2);4次矩阵加法,每个矩阵中的元素个数为n² / 4, 用时θ(n²);其余用时θ(1)。因此共用时8T(n/2) + θ(n²)。
可解得,T(n) = θ(n³)。可看出分治算法并不优于普通矩阵乘法
Strassen算法分析与上面基本一致,不同的是只进行了7次递归,并且额外多了几次n / 2 × n / 2矩阵的加法,但只是常数次。Strassen算法用时为:
可解得,T(n) = θ(n^lg7);
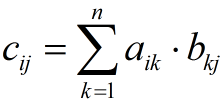

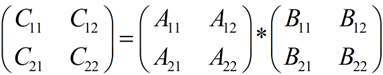


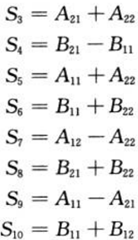
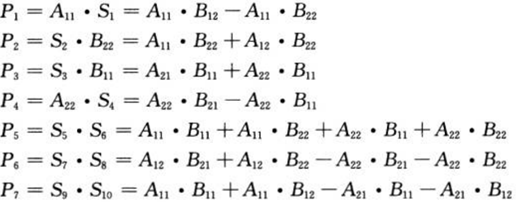
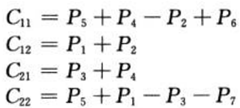
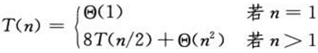
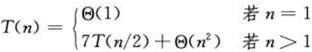

 浙公网安备 33010602011771号
浙公网安备 33010602011771号