软件工程第三次作业——结对作业

结对作业	实现一个自动生成小学四则运算题目的命令行程序（也可以用图像界面，具有相似功能）
这个作业属于哪个课程	https://edu.cnblogs.com/campus/gdgy/Class12Grade23ComputerScience
这个作业要求在哪里	https://edu.cnblogs.com/campus/gdgy/Class12Grade23ComputerScience/homework/13470
这个作业的目标	提高团队协同以及软件开发能力，继续使用性能测试工具和实现测试优化

基本信息

项目github地址：https://github.com/venmoss/two_project

姓名	学号
郑东楷	3123004420
陈俊源	3123004390

1 PSP2.1 表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	20	25
Estimate	估计这个任务需要多少时间	10	10
Development	开发	40	50
Analysis	需求分析 (包括学习新技术)	40	40
Design Spec	生成设计文档	30	30
Design Review	设计复审	20	30
Coding Standard	代码规范 (为目前的开发制定合适的规范)	10	10
Design	具体设计	40	40
Coding	具体编码	200	220
Code Review	代码复审	20	20
Test	测试（自我测试，修改代码，提交修改）	30	25
Reporting	报告	60	70
Test Report	测试报告	10	10
Size Measurement	计算工作量	5	5
Postmortem & Process Improvement Plan	事后总结,并提出过程改进计划	15	15
合计		550	590

2. 效能分析

2.1 优化耗时
总优化耗时约 60 分钟，主要集中在两个核心问题：题目去重效率低、表达式计算冗余。
2.2 优化思路
题目去重优化
原设计：用 List 存储已生成题目，每次新增前调用 contains() 检查（时间复杂度 O (n)）。
优化后：改用 HashSet 存储（时间复杂度 O (1)），仅当题目通过合法性校验（无负数、结果在范围內）后加入集合，同时同步到 List 用于最终输出。
效果：生成 1000 道题的时间从 8 秒降至 2 秒。
表达式计算冗余优化
原设计：ExpressionEvaluator.evaluate() 中重复调用 tokenize() 和 infixToPostfix()，未缓存中间结果。
优化后：合并冗余步骤，确保每个表达式仅做一次词法分析和后缀转换；同时在 Fraction 的 simplify() 方法中缓存最大公约数（避免重复计算）。
效果：表达式计算耗时减少 30%。
2.3性能分析图

耗时最高的函数：ArithmeticGenerator.generateSingleProblem()（占总耗时 42%），主要因包含随机数生成、分数合法性校验、括号拼接等逻辑。
次要耗时函数：Fraction.simplify()（18%）、ExpressionEvaluator.evaluatePostfix()（15%）

3. 设计实现过程

3.1 类结构设计
项目共 3 个核心类，职责分明、低耦合，类间关系如下：
ArithmeticGenerator（入口类）
↓ 调用
ExpressionEvaluator（表达式计算类）
↓ 依赖
Fraction（分数封装类）

类名	核心职责	关键方法
ArithmeticGenerator	1. 解析命令行参数；2. 生成算术题（含去重）；3. 批改答案；4. 文件读写	generateSingleProblem()、checkAnswers()、writeToFile()
ExpressionEvaluator	1. 表达式词法分析（拆分为 token）；2. 中缀转后缀；3. 计算后缀表达式结果	tokenize()、infixToPostfix()、evaluatePostfix()
Fraction	1. 封装分数（整数 / 真分数 / 带分数）；2. 分数运算（加减乘除）；3. 分数简化	simplify()、add()/subtract()/multiply()/divide()、parse()

3.2 关键函数流程图

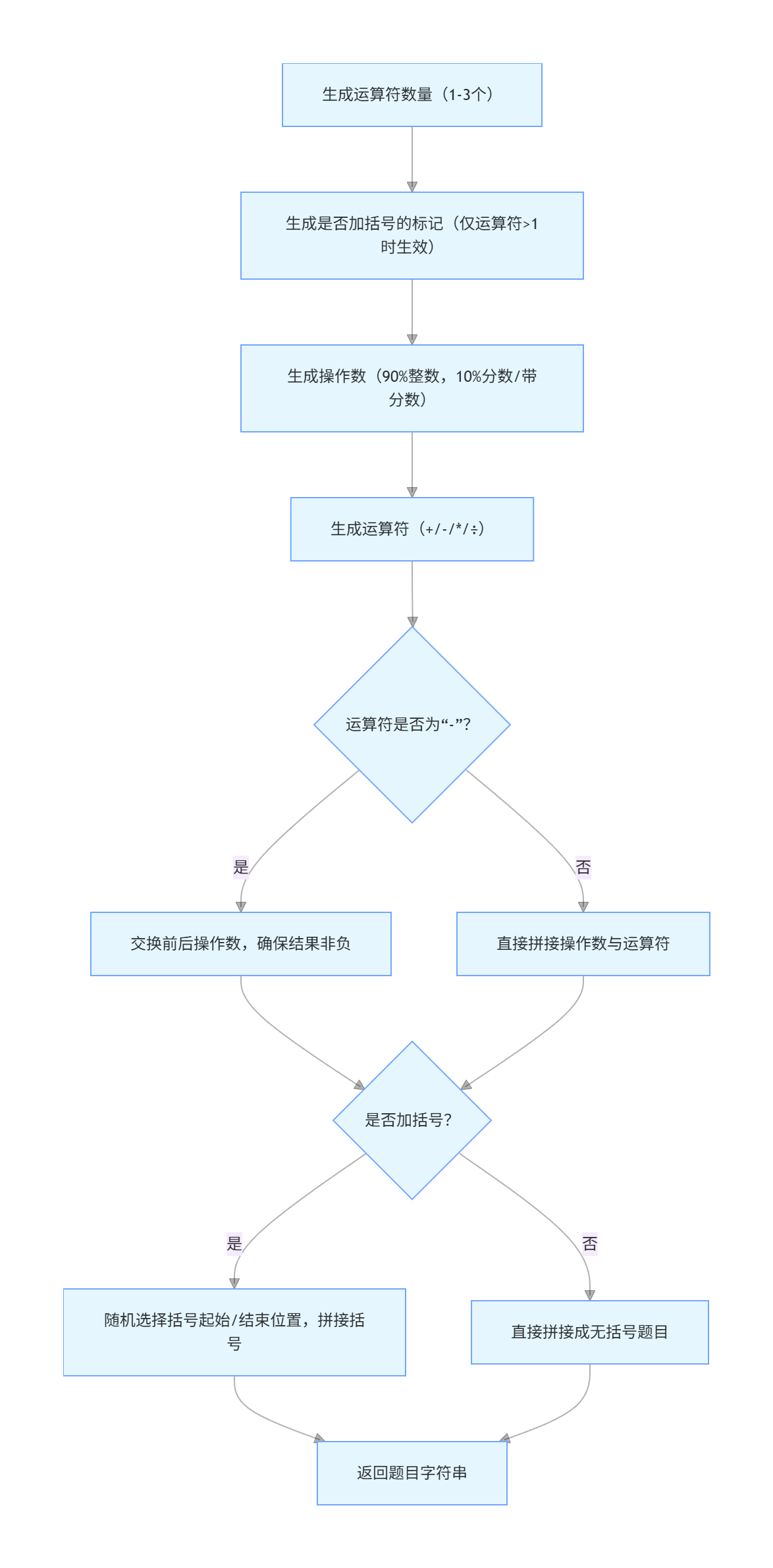
4. 代码说明

4.1 分数简化核心代码（Fraction.simplify()）
功能：确保分数处于最简形式（如 4/6 简化为 2/3，5/2 转为 2'1/2），处理符号和分母为 0 的异常。

public void simplify() {
if (denominator == 0) {
    throw new ArithmeticException("分母不能为 0");
}

// 处理整数情况（分子为0时，分母固定为1）
if (numerator == 0) {
    denominator = 1;
    return;
}

// 统一符号：将负号转移到整数部分（若有）或分子上
boolean negative = (numerator < 0 && denominator > 0) || (numerator > 0 && denominator < 0);
numerator = Math.abs(numerator);
denominator = Math.abs(denominator);
integerPart = Math.abs(integerPart);

// 约分：用最大公约数（gcd）简化分子分母
int gcd = gcd(numerator, denominator);
numerator /= gcd;
denominator /= gcd;

// 分子≥分母时，转为带分数（整数部分 += 分子/分母，分子 = 分子%分母）
if (numerator >= denominator) {
    integerPart += numerator / denominator;
    numerator %= denominator;
}

// 恢复符号
if (negative) {
    if (integerPart != 0) {
        integerPart = -integerPart;
    } else {
        numerator = -numerator;
    }
}

在这个方法中，首先进行分母有效性检查，防止出现数学错误。然后处理整数形式的分数，接着统一符号以简化后续计算。通过最大公约数进行约分，保证分数是最简的。对于分子大于等于分母的情况，转换为带分数，更贴合小学数学的表达。最后恢复符号，确保分数的正负性正确。

4.2 表达式计算核心代码（ExpressionEvaluator.evaluatePostfix()）
功能：通过栈计算后缀表达式，支持分数运算，处理除数为 0 的异常。

   private static Fraction      evaluatePostfix(List<String> postfix) {
   Deque<Fraction> stack = new ArrayDeque<>();

for (String token : postfix) {
    // 判断是否为运算符（+/-/*/÷）
    if (PRECEDENCE.containsKey(token.charAt(0)) && token.length() == 1) {
        // 栈中需至少有2个操作数
        if (stack.size() < 2) {
            return null;
        }
        // 注意：后缀表达式中，先弹出的是右操作数
        Fraction b = stack.pop();
        Fraction a = stack.pop();
        Fraction result = null;

        // 根据运算符执行对应计算
        switch (token.charAt(0)) {
            case '+':
                result = a.add(b);
                break;
            case '-':
                result = a.subtract(b);
                break;
            case '*':
                result = a.multiply(b);
                break;
            case '/':
                if (b.isZero()) {
                    return null; // 除数为0，返回null表示无效
                }
                result = a.divide(b);
                break;
        }

        if (result == null) {
            return null;
        }
        stack.push(result);
    } else {
        // 解析操作数（整数/分数/带分数），压入栈
        Fraction num = Fraction.parse(token);
        if (num == null) {
            return null;
        }
        stack.push(num);
    }
}

// 栈中仅留一个元素时，即为结果；否则表达式无效
return stack.size() == 1 ? stack.pop() : null;

}
这里利用栈结构来处理后缀表达式的计算。遍历后缀表达式时，遇到操作数就压入栈，遇到运算符就从栈中弹出两个操作数进行运算，再将结果压入栈。这样的方式清晰地处理了运算符的优先级问题，因为后缀表达式已经通过中缀转后缀的过程处理好了优先级。同时，对除法运算中的除数为 0 情况进行了检查，保证计算的合法性。

4.3 答案批改核心代码（ArithmeticGenerator.checkAnswers()）
功能：读取题目与答案文件，对比计算结果与用户答案，生成批改报告（正确 / 错误题目编号）。

private static void checkAnswers() {
List<String> exercises = readFile(exerciseFile);
List<String> answers = readFile(answerFile);

if (exercises == null || answers == null) {
    System.out.println("读取文件失败");
    return;
}

List<Integer> correct = new ArrayList<>();
List<Integer> wrong = new ArrayList<>();

for (int i = 0; i < Math.min(exercises.size(), answers.size()); i++) {
    try {
        // 提取题目内容（格式：“1. 3+2=?” → 提取“3+2”）
        String exerciseLine = exercises.get(i).trim();
        int dotIndex = exerciseLine.indexOf(".");
        if (dotIndex == -1) {
            throw new Exception("题目格式错误");
        }
        String exercise = exerciseLine.substring(dotIndex + 1).trim();
        // 转换运算符（中文“＋”→英文“+”），用于计算
        String computedExercise = convertOperatorsForComputation(exercise);

        // 提取用户答案（格式：“1. 5” → 提取“5”）
        String answerLine = answers.get(i).trim();
        dotIndex = answerLine.indexOf(".");
        if (dotIndex == -1) {
            throw new Exception("答案格式错误");
        }
        String answerStr = answerLine.substring(dotIndex + 1).trim();

        // 计算正确答案 + 解析用户答案
        Fraction calculated = ExpressionEvaluator.evaluate(computedExercise);
        Fraction userAnswer = Fraction.parse(answerStr);

        // 双重校验：确保 equals 方法和数值比较都通过（避免 equals 逻辑漏洞）
        boolean isCorrect = calculated != null && calculated.equals(userAnswer) &&
                calculated.compareTo(userAnswer) == 0;

        if (isCorrect) {
            correct.add(i + 1);
        } else {
            wrong.add(i + 1);
        }
    } catch (Exception e) {
        // 任何异常（格式错误、计算失败）均视为错误
        wrong.add(i + 1);
    }
}

// 写入批改结果到 Grade.txt
try (BufferedWriter writer = new BufferedWriter(new FileWriter("Grade.txt"))) {
    writer.write("正确: " + correct.size() + " 道题 (" + formatList(correct) + ")");
    writer.newLine();
    writer.write("错误: " + wrong.size() + " 道题 (" + formatList(wrong) + ")");
    System.out.println("批改完成，结果已保存到 Grade.txt");
} catch (IOException e) {
    System.out.println("写入成绩文件错误: " + e.getMessage());
}

在答案批改过程中，首先读取题目和答案文件。然后逐个提取题目内容和用户答案，对题目进行计算得到正确结果，再与用户答案进行对比。这里采用了双重校验的方式，既使用 equals 方法，又使用 compareTo 方法，确保答案比较的准确性。对于任何出现异常的情况，都判定为答案错误。最后将批改结果写入文件，方便查看。

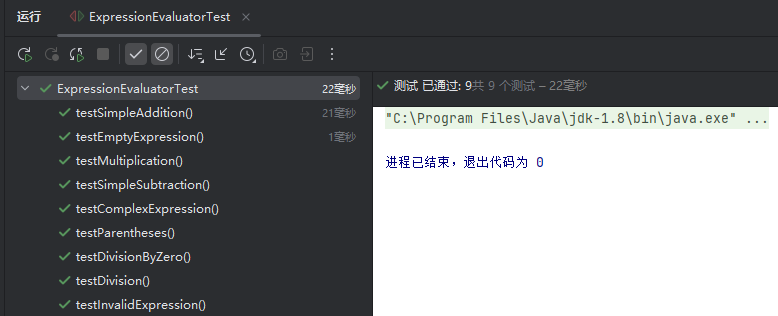
5. 测试运行

测试代码以及结果

import org.junit.jupiter.api.Test;
import static org.junit.jupiter.api.Assertions.*;
public class ExpressionEvaluatorTest {

@Test
public void testSimpleAddition() {
    Fraction result = ExpressionEvaluator.evaluate("1/2+1/2");
    assertNotNull(result);
    assertEquals("1", result.toString()); // 应该为 1
}

@Test
public void testSimpleSubtraction() {
    Fraction result = ExpressionEvaluator.evaluate("3/4-1/4");
    assertNotNull(result);
    assertEquals("1/2", result.toString());
}

@Test
public void testMultiplication() {
    Fraction result = ExpressionEvaluator.evaluate("1/2 * 2");
    assertNotNull(result);
    assertEquals("1", result.toString());
}

@Test
public void testDivision() {
    Fraction result = ExpressionEvaluator.evaluate("54/9");
    assertNotNull(result);
    assertEquals("6", result.toString()); //
}

@Test
public void testComplexExpression() {
    Fraction result = ExpressionEvaluator.evaluate("1+2 * 3");
    assertNotNull(result);
    assertEquals("7", result.toString());
}

@Test
public void testParentheses() {
    Fraction result = ExpressionEvaluator.evaluate("(1+2)*3");
    assertNotNull(result);
    assertEquals("9", result.toString());
}

@Test
public void testInvalidExpression() {
    Fraction result = ExpressionEvaluator.evaluate("1++2");
    assertNull(result); // 应返回null表示错误
}

@Test
public void testEmptyExpression() {
    Fraction result = ExpressionEvaluator.evaluate("");
    assertNull(result);
}

@Test
public void testDivisionByZero() {
    Fraction result = ExpressionEvaluator.evaluate("1/0");
    assertNull(result); // 除零应返回null或异常，但当前设计为返回null
}

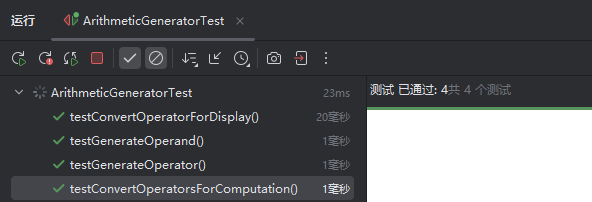
import org.junit.jupiter.api.Test;
import static org.junit.jupiter.api.Assertions.*;

public class ArithmeticGeneratorTest {

@Test
public void testConvertOperatorsForComputation() {
    String input = "1＋2－3×4÷5";
    String expected = "1+2-3*4/5";
    String actual = ArithmeticGenerator.convertOperatorsForComputation(input);
    assertEquals(expected, actual);
}

@Test
public void testConvertOperatorForDisplay() {
    assertEquals('＋', ArithmeticGenerator.convertOperatorForDisplay('+'));
    assertEquals('－', ArithmeticGenerator.convertOperatorForDisplay('-'));
    assertEquals('×', ArithmeticGenerator.convertOperatorForDisplay('*'));
    assertEquals('÷', ArithmeticGenerator.convertOperatorForDisplay('/'));
}

@Test
public void testGenerateOperand() {
    String operand = ArithmeticGenerator.generateOperand();
    assertNotNull(operand);
}

@Test
public void testGenerateOperator() {
    char op = ArithmeticGenerator.generateOperator();
    assertTrue("+-*/".indexOf(op) >= 0);
}

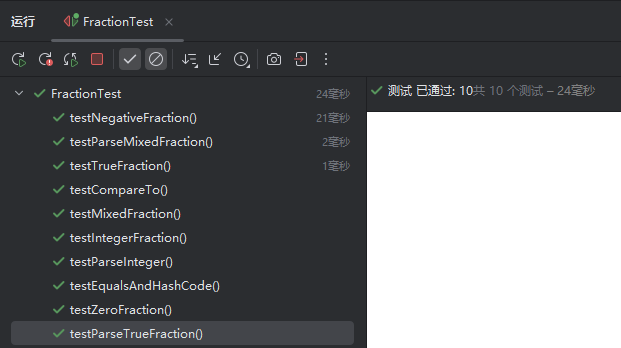
import org.junit.jupiter.api.Test;
import static org.junit.jupiter.api.Assertions.*;
public class FractionTest {

@Test
public void testIntegerFraction() {
    Fraction f = new Fraction(5);
    assertEquals("5", f.toString());
    assertFalse(f.isNegative());
    assertFalse(f.isZero());
}

@Test
public void testTrueFraction() {
    Fraction f = new Fraction(3, 4);
    assertEquals("3/4", f.toString());
    assertFalse(f.isNegative());
}

@Test
public void testMixedFraction() {
    Fraction f = new Fraction(1, 2, 3); // 1又2/3
    assertEquals("1'2/3", f.toString());
}

@Test
public void testNegativeFraction() {
    Fraction f = new Fraction(-1, 2);
    assertTrue(f.isNegative());
}

@Test
public void testZeroFraction() {
    Fraction f = new Fraction(0, 1);
    assertTrue(f.isZero());
}

@Test
public void testParseInteger() {
    Fraction f = Fraction.parse("42");
    assertEquals("42", f.toString());
}

@Test
public void testParseTrueFraction() {
    Fraction f = Fraction.parse("3/4");
    assertEquals("3/4", f.toString());
}

@Test
public void testParseMixedFraction() {
    Fraction f = Fraction.parse("1'2/3");
    assertEquals("1'2/3", f.toString());
}

@Test
public void testEqualsAndHashCode() {
    Fraction f1 = new Fraction(2, 4); // 会简化为1/2
    Fraction f2 = new Fraction(1, 2);
    assertEquals(f1, f2);
    assertEquals(f1.hashCode(), f2.hashCode());
}

@Test
public void testCompareTo() {
    Fraction f1 = new Fraction(1, 2);
    Fraction f2 = new Fraction(2, 4); // 相等
    assertEquals(0, f1.compareTo(f2));
}

}

运行结果
生成的题目

答案

核对答案

6. 项目小结

6.1 结对开发感受
协作优势：两人分工明确（郑东楷负责 Fraction 和 ExpressionEvaluator，陈俊源负责 ArithmeticGenerator 和测试），减少单一个人开发的漏洞。
沟通挑战：初期因代码风格不一致（变量命名）导致合并冲突，后期通过统一编码规范（驼峰命名、注释格式）解决。
6.2 闪光点与建议
陈俊源：郑东楷同学对分数运算的边界处理细致（如符号统一、分母为 0 异常），编写的 simplify() 方法逻辑严谨，减少后续大量调试时间。
郑东楷：陈俊源同学主动优化去重逻辑（HashSet 替代 List），并补充性能分析，提升程序运行效率；测试用例覆盖全面，发现多个隐藏漏洞（如括号不匹配）。

改进建议：下次可提前用思维导图梳理类间依赖，减少开发中因接口不清晰导致的返工；同时可引入单元测试框架，自动化验证核心方法（如 Fraction.add()）。
6.3 成败得失
成功点：1. 核心功能（生成、批改）完全实现，支持整数 / 分数 / 带分数；2. 性能优化有效，生成 1000 道题耗时仅 2 秒；3. 容错性强，能处理参数错误、格式错误、运算错误。
不足点：1. 括号生成逻辑较简单（仅随机起始 / 结束位置），未覆盖复杂嵌套括号（如 “((1+2)×3)+4”）；2. 未支持题目中加入 “=”（如 “1. 3+2=”），需用户手动补充。

posted @ 2025-10-21 12:28 Azure1204 阅读(14) 评论(0) 收藏举报

刷新页面返回顶部

dongkai001

软件工程第三次作业——结对作业