计算机图形学 opengl版本 第三版------胡事民 第四章 图形学中的向量工具
一 基础
1：向量分析和变换 两个工具 可以设计出各种几何对象
点和向量基于坐标系定义
拇指指向z轴正方向 从x轴的正向握向y轴的正向， 可以分为左手和右手坐标系。
点A到点B的位移称为向量v 则v=B-A 尾-头
一个n维向量是一个n元组 w=(w1,w2,w3,...)
用矩阵来表示向量 更加方便清晰
2：向量的基本运算法则
向量a b 标量s （实数） a=(a1,a2,a3) (向量的坐标表示) b=(b1,b2,b3)
加法:a+b= (a1+b1,a2+b2,a3+b3)
乘法：s(a)=(s*a1,s*a2,s*a3)
有些系统中 标量s表示复数 这里不讨论
3. 向量的线性组合
m个向量v1，v2，v3...vm
向量w=a1v1+a2v2+a3v3+...am+vm
其中am为标量
特殊的线性组合：仿射组合 凸组合
向量的仿射组合：标量系数的和为1 且仅和标量有关
a1+a2+a3+...+am=1
两个向量a和b的仿射组合形式
(1-t)a+(t)b
向量的凸组合：标量的和为1 且 各个标量>=0
4.向量的度量和单位向量
w为向量
|w|=根号下（w1^2+w2^2+w3^2+....+wn^2） 勾股定理 模为头尾两点的距离
有时需要缩放向量 使向量的长度为一，这一过程被叫做向量的归一化 归一化的结果为单位向量
为了得到a的归一化向量 我们可以用1/|a|数乘a
a的单位向量=a/|a| 其中|a|!=0
例如：a=(3,-4) 那么|a|=5 归一化的结果为a^=(3/5,-4/5) 有时我们也吧单位向量看成方向。
任何一个向量都可以写成：a=|a|a^ 向量的模乘方向
二.点积
1.两个工具 点积 和叉积
点积得到一个标量，用于二维向量
叉积得到一个向量 用于三维向量
a.b=a1b1+a2b2
定义：
n维向量v=（v1,v2,v3...vn） w=（w1，w2,w3...wn）
点积d表示为v.w=v1.w1+v2.w2+...vn.wn
性质：对称性（交换）：a.b=b.a
线性：（a+c）.b=a.b+c.b
同质性：（s.a）.b=s(a.b)
|b|.|b|=b.b
2.两向量的夹角：
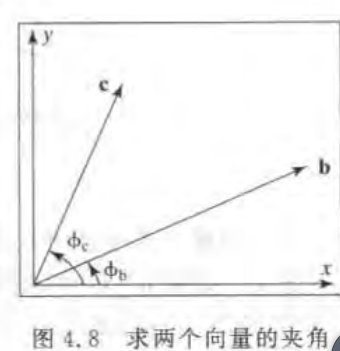
b=(|b|cos∠b，|b|sin∠b)
c=(|c|cos∠c，|c|sin∠c)
b.c=|b|.|c|.cos∠c.cos∠b+|b|.|c|.sin∠c.sin∠b
b.c=|b|.|c|.cos∠boc
上式两边同时除以|b||c|
cos(∠boc)=b^.c^ 两个向量b和c之间的夹角的余弦等于归一化后向量的点积
3.b.c的符号和正交性
b.c>0 角度小余90度
b.c=0 角度等于90度 此时b垂直于c 则称向量b和向量c是正交的。
b.c<0 角度大于90度
正交也叫直交或者垂直
三维形式常用 叫做标准单位向量,分别称为 i j k
定义：三维空间的标准单位向量有如下分量的向量
i=(1,0,0) j=(0,1,0) k=(0,0,1) 也可以写成矩阵的形式
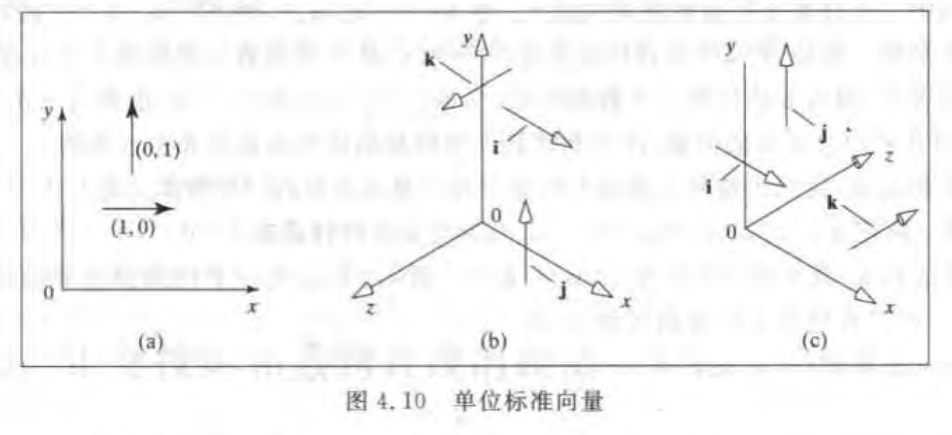
任意一个三维向量如（a,b,c）都可以写成另一种形式
(a,b,c)=ai+bj+ck
4.二维正交向量
a=(ax,ay)的正交向量为b(-ay,ax) 导致a.b=0 两个向量垂直 ⊥
与a向量的正交向量有无穷多个 任何一个数成b的结果都是与a正交的
定义：给定a=(ax,ay) 则a⊥ =（-ay,ax） 与a逆时针正交
a像左转90度a⊥ a想右转90度为-a⊥
a⊥ 的一些有趣的属性
1.线性 （ a+b）⊥ =a⊥ +b⊥ 对任意标量A 有（Aa）⊥ =Aa⊥
2.a⊥⊥ =（a⊥ ）⊥ = - a
3. 正交点积 a⊥ .b=axby-aybx 其中a=（ax,ay）
a⊥ .a=0
|a⊥ |^2=|a|^2 两正交向量具有相同的长度
a⊥ .b=-b⊥ .a 反对称性 例如（0,1） 和（-1,0） 为反对称性
4.
行列式
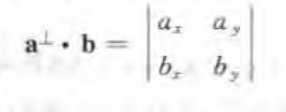
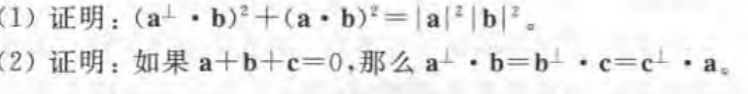
上面的两个证明 将坐标带入后化简即可得到
5.正交投影和点到直线的距离
图形学中常出现的问题
a 将一个向量投影到另一个向量上
b 将一个向量分解成不同方向上的分量
c 找到一点到另一条直线的距离
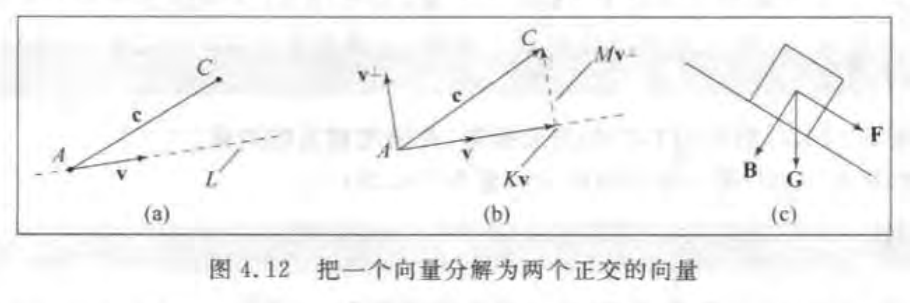
k和m是待定的常数 c=kv+mv⊥
我们说从c到v的正交投影是kv并且点c到直线的距离是|mv⊥|
求出k和m 的方法：等式两边同时乘以一个v
c.v=kv.v+v.mv⊥
k=c.v/v.v
两边同时乘以 v⊥
m=c.v⊥/v⊥.v⊥
距离=m .v⊥
也等于 
例题：4.3.5
将向量c(6,4)到v=（1,2）的正交投影 并画出相关的向量
用4.20的公式：（14/5,28/5）
例题：4.3.6
求点c=(6,4)到过点（1,1）和（4,9）的直线的距离
6.投影的应用：反射
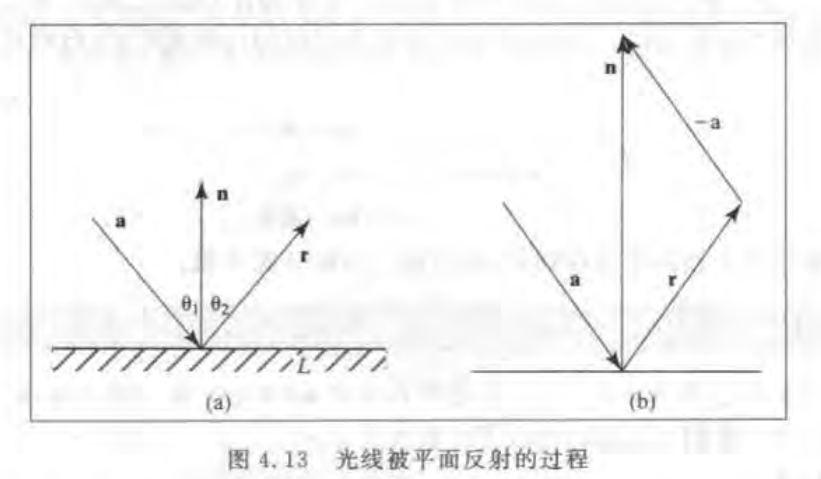
入射角等于出射角
