2018/11/19--2018/11/26周学习内容

首先我将书上的六个例题都看了一遍，读懂意思以后也都敲了一遍

 

3．2．1兔子繁殖问题
（题目来：JLO이2337）
1．问题描述
【Description】
  这是一个有趣的古典数学问题，著名意大利数学家 Fibonacci曾提出一个问题：有一对
  小兔子，从出生后第3个月起每个月都生一对兔子。小兔子长到第3个月后每个月又生
  对兔子。按此规律，假设兔子没有死亡，第一个月有一对刚出生的小兔子，问第n个月有
  多少对兔子？
【Input】
  输入月数n（1≤n≤45）。
【output】
  输出第n个月有多少对兔子。
【Sample Input】
  6
【Sample Output】
  8

解析：感觉这个兔子繁殖问题和斐波那契数列一样，说的很厉害的样子，但是真的计算起来和斐波那契数列的计算过程也是一样的。

代码：

 

 1 #include <stdio.h>
 2 //兔子繁殖（斐波那契数列）
 3 int main(void)
 4 {
 5     int n,b=1,d=1,z,i;
 6     scanf("%d",&n);
 7     for (i = 3; i < n; i++)
 8     {
 9         z=d;
10         d=b+d;
11         b=z;
12     }
13     printf("%d\n",d );
14     return 0;
15 }

 

3．2．2最大公约数问题
（题目来源：JLOJ2338）
1．问题描述
【 Description】
  任意给两个正整数m和n，求它们的最大公约数。
【input】
  输入两个正整数m和m。
【 Output】
  输出m和n的最大公约数。
【Sample Input】
  12  18
【Sample Output】
  6

 解析：这个好像利用到了高中学习的辗转相除法，在这段代码里面我写了g（公）b（倍）s（数）的函数，先把两个数的大小比较出来，然后在被除数不为零的前提下一直取余，最终等到y为零以后返回x这个最大公倍数。

代码：

 

#include <stdio.h>
//最大公倍数
int gbs(int x,int y);

int main(void)
{
    int a,b,z;
    scanf("%d%d",&a,&b);
    z=gbs(a,b);
    printf("%d\n",z );
    return 0;
}

int gbs(int x,int y)
{
    int m;
    if (x<y)
    {
        m=x;
        x=y;
        y=m;
    }
    while(y>0){
        m=x%y;
        x=y;
        y=m;
    }
    return x;
}

 

 

 

 

 

这一部分是课后的习题啦

 

3．3．1求年龄
（题目源：LO2416）
【Description】
  有n个人围坐在一起，当问第n个人的年龄时，他说比第n－1个人大2岁。问第n－1
  个人的年龄时，他说比第m－2个人大2岁。向第n－2个人时，他又说比第n－3个人大2
  岁……最后问到第一个人时，他说是10岁。请问第n个人的年龄？
【Input】
  输入一个正整数n（n＜40）。
【 Output】
  输出第n个人的年龄。
【Sample Input】

  5
【Sample Output】
  18

 

分析：这道题就是由第一个递加，加到了第n个，这没什么好说的

代码：

 1 #include <stdio.h>
 2 //3.3.1  求年龄
 3 
 4 int main(void)
 5 {
 6     int n,a=10,i;
 7     scanf("%d",&n);
 8     for (i = 1; i < n; i++)
 9     {
10         a=a+2;
11     }
12     printf("%d\n",a);
13     return 0;
14 }

 

运行结果：

 

3．3．2斐波那契数列求和
（题目来源：JLO2417）
【Description】
  求斐波那契数列的前n项之和。
【input】
  输入一个正整数n（0＜n＜100）。
【 Output】
  输出前n项的和。
【Sample Input】
  5
【Sample Output】
  12

分析：斐波那契数列我写过很多次了，有用递归的方法还有用非递归的方法写过。这次是用递推方法写的，我利用了一个for循环来把前一百个数据存进了数组里，然后又利用一个for循环把前n项数据都加到了sum里面。

代码：

 1 #include <stdio.h>
 2 //3.3.2 斐波那契数列求和
 3 
 4 int main(void)
 5 {
 6     int a[101],i,sum,n;
 7     a[1]=1;
 8     a[2]=1;
 9     sum=0;
10     scanf("%d",&n);
11     for (i = 3; i < 101; i++)
12     {
13         a[i]=a[i-1]+a[i-2];
14     }
15     for (i = 1; i <= n; i++)
16     {
17         sum+=a[i];
18     }
19     printf("%d\n",sum);
20     return 0;
21 }

 

 运行结果：

 

 

3．3．3绝不后退
（题目来源：JLOJ2418）
【 Description】
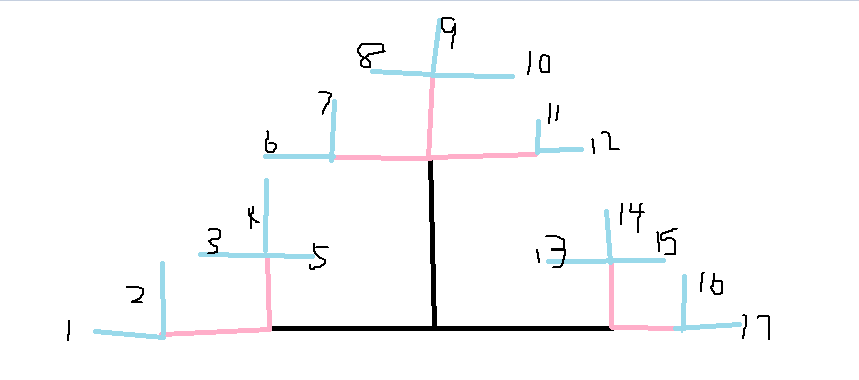
  从原点出发，一步只能向右走、向上走或向左走，每步都只能走一个单位长度。恰
  走N步且不经过已走的点共有多少种走法？
【Input】
  每行一个整数N，代表步数，0＜Nk20。
【 Output】
  输出共有多少种走法。
【Sample Input】
  3
【Sample Output】
  10

分析： 画图来说明，请叫我灵魂画手哈哈哈。我先画图列举了前五次的选择（当然是在草纸上画的），先列举然后再找规律。不知道书上是什么思路，反正照我这个思路写，结果和书上的好像有点不一样。

代码：

 1 #include <stdio.h>
 2 //3.3.3 决不后退
 3 
 4 int main(void)
 5 {
 6     int a[20],n,i;
 7     a[1]=3;
 8     a[2]=7;
 9     scanf("%d",&n);
10     for (i = 3; i <= n; i++)
11     {
12         a[i]=a[i-2]+a[i-1]*2;
13     }
14     printf("%d\n",a[n]);
15     return 0;
16 }

运行结果：

 

 

 3．3．4取数
（题目来：JLO］2419）
【 Description】
  自然数从1到N按照顺序排成一排，可以从中取走任意数，但是相邻的两个数不可以
  司时被取走。一共有多少种取法？
【Input】
  输入一个正整数N（N＜20）。
【 Output】
  输出取数的取法总数。
【 Sample Input】
  15
【 Sample Output】
  1596
分析：这个我先一个一个在本子上面列举了，我感觉有些像斐波那契数列，但是我列举的情况总是比斐波那契数列的值少一。

代码：

#include <stdio.h>
//取数

int main(void)
{
    int a[21],n,i,b;
    a[1]=2;
    a[2]=3;
    scanf("%d",&n);
    for (i = 3; i<20; i++)
    {
        a[i]=a[i-2]+a[i-1];
    }
    b=a[n]-1;
    printf("%d\n",b);
    return 0;
}

运行结果：

 

 

3．3．5王小二的刀
（题目来：JLO2420）
【Description】
  王小二自夸刀工不错，有人放一张大的煎饼在砧板上，问他：“饼不许离开砧板，切n
（1≤n≤100）刀最多能分成多少块？”
【input】
  输入正整数n（1≤n≤100），n代表切煎饼的刀数
【output】
  输出n刀切的块数。

【Sample Input】
  5
【Sample Output】
  16

分析：这个没什么好说的，先列举了前几种方法，然后找到了规律，其实就是一个数学问题。

代码：

#include <stdio.h>
//王小二的刀

int main(void)
{
    int n,a;
    scanf("%d",&n);
    a=n*(n+1)/2+1;
    printf("%d\n",a);
    return 0;
}

运行结果：