模式识别第一次作业
1.1
(a)由题意：\(\frac{8a-1}{3}\geq 0\)得：\(a\geq \frac{1}{8}\)
(b)答案为1
(c)考虑将分母中的\(3\)消去：当\(a=\frac{1}{2}\)时，答案为1，当\(a=2\)时，答案为\(\sqrt{5}\)，当\(a=5\)时，答案为\(\sqrt{13}\)。猜想：解为\(\sqrt{\frac{8a-1}{3}}\)
(d)octave中返回1.21825 + 0.12600i
(e)由于三次方根存在三个，而原始程序中保留的是x轴正方向开始逆时针旋转的第一个向量。正确答案为1.2910。通过程序验证，猜想正确。
(f)证明：设\(x=\frac{1}{2}\sqrt{\frac{8a-1}{3}}\)，\(y=\frac{1}{2}\)，则原式\(=((x+y)^3)^{\frac{1}{3}}-((x-y)^3)^{\frac{1}{3}}=2x\)
(g)\((2+\sqrt{5})^{\frac{1}{3}}+(2-\sqrt{5})^{\frac{1}{3}}=(\frac{\sqrt{5}+1}{2})^{3*\frac{1}{3}}+(\frac{\sqrt{5}-1}{2})^{3*\frac{1}{3}}=\sqrt{5}\)
(h)无论是Cardano用于解三次方程的方法还是本问题的方法本质都是构造，三次根号里面的式子结构一样，只是前者更巧妙一些，而本题是靠从简单到一般推出来的。
2.1
(a)根据投影定义：\(\Vert \boldsymbol x_\perp\Vert=\frac{\boldsymbol x^T \boldsymbol y}{\Vert \boldsymbol x \Vert}=\frac{(\sqrt {3},1)^T( 1, \sqrt{3})}{2}=\sqrt{3}\)，且\(\boldsymbol x_\perp\)与\(\boldsymbol y\)同向，故：$ \boldsymbol x_\perp=(\frac{\sqrt{3}}{2},\frac{3}{2})$
(b) \(\because\) $ \boldsymbol y^T(\boldsymbol x- \boldsymbol x_\perp)=(1,\sqrt{3})^T(\frac{\sqrt{3}}{2},-\frac{1}{2})=0$ \(\therefore\) $ \boldsymbol y\perp (\boldsymbol x- \boldsymbol x_\perp)$
(c)
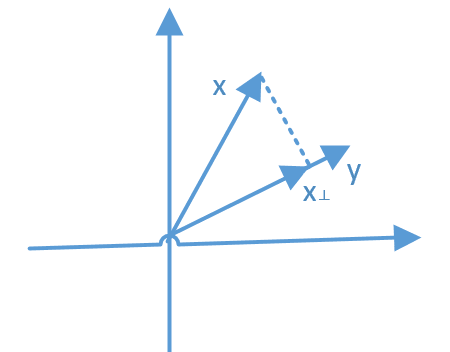
(d)由题意知，当\(\boldsymbol x_\perp=\lambda \boldsymbol y\)时，不等式取等号，当\(\boldsymbol x_\perp \neq \lambda \boldsymbol y\)时，根据c题中的图，向量\(\boldsymbol x- \boldsymbol x_\perp\)、\(\boldsymbol x_\perp-\lambda \boldsymbol y\)、\(\boldsymbol x-\lambda \boldsymbol y\)构成一个直角三角形，且\(\boldsymbol x-\lambda \boldsymbol y\)为斜边，因此\(\Vert \boldsymbol x- \boldsymbol x_\perp\Vert<\Vert \boldsymbol x- \lambda\boldsymbol y\Vert\)，综上所述：
2.2
(a)由于正定矩阵的特征值全部为正数，因此\(X\)为正定矩阵的充要条件为\(x>0\)
(b)根据公式\(det(X)=\Pi_{i=1}^{n}\lambda_i\)，即\(X\)的行列式为其所有特征值之积，因此\(1*1*3*4*x=72\)得：\(x=6\)
2.6
(a)\(E(X)=\int_{-\infty}^{+\infty}x*f(x)dx=\int_{-\infty}^{+\infty}\beta xe^{-\beta x}dx=\int_{0}^{+\infty}\beta xe^{-\beta x}dx=\frac{1}{\beta}\)（分步积分）
\(D(X)=E(X^2)-(EX)^2=\int_{0}^{+\infty}\beta xe^{-\beta x^2}dx-\frac{1}{\beta^2}=\frac{1}{2}-\frac{1}{\beta^2}\)
(b)由\(F(x)=P(X\le x)=\int_{-\infty}^{x}p(x)dx\)得，\(x<=0\)时，\(F(x)=0\)
\(x>0\)时，\(F(x)=\int_{0}^{x}f(x)dx=\int_{0}^{x}\beta e^{-\beta x}dx=1-e^{-\beta x}\)，故：
(c)\(P_r(X\geq a+b|X\geq a)=\frac{P_r(X\geq a+b,X\geq b)}{P_r(X\geq a)}=\frac{P_r(X\geq a+b)}{P_r(X\geq a)}=\frac{1-F(a+b)}{1-F(a)}=e^{-bx}\),\(P_r(x\geq b)=1-F(b)=e^{-bx}\),因此\(P_r(X\geq a+b|X\geq a)=P_r(x\geq b)\)
(d)根据(a)中的计算，灯泡期望的寿命为1000小时，根据(c)中证明的指数分布无记忆性可知，灯泡虽然使用了2000小时，但其剩余寿命的期望仍然是1000小时。
2.10 证明凹凸函数采用引理：判断函数二阶导数的正负
(a)\(f(x)^{''}=a^2e^{ax}\geq 0\)，故对任意实数\(a\in R，\)f(x)$为凸函数
(b)\(f(x)^{''}=-\frac{1}{x^2}\)，对于\(x>0\)，二阶导数恒负，故在该范围内是凹函数
(c)\(h(x)^{''}=\frac{1}{x}\)，在\(x\geq 0\)时二阶导数非负，因此函数在该范围内为凸函数。
(d)设L函数：\(L(p_1,p_2,...,p_n,\lambda)=-\sum_{i=1}^{n}p_i\log_2p_i+\lambda(\sum_{i=1}^{n}p_i-1)\)（根据离散分布概率和为1），分别对\(p_i\)以及\(\lambda\)求导得：
解得：\(p_1=p_2=...=p_n=\frac{1}{n}\)，此时得到\(H\)最大值为\(-\sum_{i=1}^{n}\frac{1}{n}\log_2 \frac{1}{n}=\log_2n\)
