POJ 计算几何入门

poj1696 Space Ant

题目链接：http://poj.org/problem?id=1696

题意：在一个二维平面上，给你n个点的坐标(Xi,Yi),已知有一条虫刚开始在(0,Ya)点，Ya为这些点中纵坐标的最小值，这只虫在这些点之间移动，只能往左走，且运动的轨迹不能有交点，每个点都要走一次，问你走这些点的轨迹，下图为一个合法的移动

 

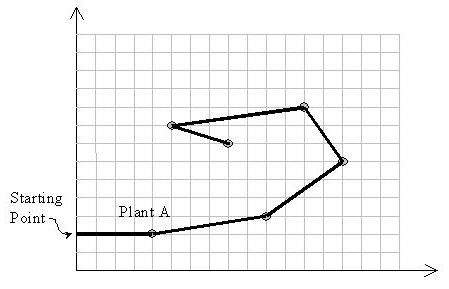
思路：通过画图容易知道这样的轨迹一定存在，第一个走的点一定是纵坐标值最小的那个点（存在多个则横坐标也是最小），我们枚举每个当前的点，这个点和它前一个走过的点构成一条线段，则剩下所有没走过的点必须在这条线段左边，否则枚举的这个点就不合法，用叉积判断一下就好，注意可能有共线的情况存在。

 

#include <cmath>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<set>
#define eps 1e-8
#define INF 1e9*1.0
#define zero(x) (((x)>0?(x):-(x))<eps)
using namespace std;
struct point{double x,y;}p[100];
struct line{point a,b;}l[1000005];
double xmult(point p1,point p2,point p0){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
int dot_online_in(point p,point l1,point l2){//判断点是否在直线上 
    return zero(xmult(p,l1,l2))&&(l1.x-p.x)*(l2.x-p.x)<eps&&(l1.y-p.y)*(l2.y-p.y)<eps;
}
int n;
set<int> ::iterator it,ite;
int main(){
    int t;
    cin>>t;
    while(t--){
        cin>>n;
        double z=1000;
        int cnt;
        int d=0;
        int a[105],x[105];
        set<int> s;
        for(int i=1;i<=n;i++){
            int k;
            cin>>k;
            cin>>p[k].x>>p[k].y;
            if(p[k].y<z){
                z=p[k].y;
                cnt=k;
            }
            s.insert(k);
            x[k]=k;
        }
        s.erase(cnt);
        a[d++]=cnt;
        x[cnt]=0;
        while(s.size()>1){
             for(int i=1;i<=n;i++)
                if(x[i]!=0)
                {
                  for(ite=s.begin();ite!=s.end();ite++){
                    if(*ite!=i){
                        if(xmult(p[i],p[*ite],p[cnt])<eps||dot_online_in(p[i],p[*ite],p[cnt]))
                            break;
                    }

                  }
                  if(ite==s.end()){
                    cnt=i;
                    s.erase(cnt);
                    x[cnt]=0;
                    a[d++]=cnt;
                  }
               }
        }
        cout<<n;;
        it=s.begin();
        if(!s.empty())
            a[d++]=*it;
        for(int  i=0;i<d;i++)
                cout<<" "<<a[i];
            cout<<endl;
    }
}

poj1981 Circle and Points

题目链接： http://poj.org/problem?id=1981

题意：给你N个点的坐标，问其中最多能找到几个点在同一个单位圆内

思路：要使最多的点在圆内，则必有两个点在圆上，由于N较小，可以暴力枚举圆上的两个点，找到圆心，再判断其他点是否在圆内。

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
const int M=310;
const double eps=1e-6;
struct point
{
 double x,y;
}p[M];
int n;
double dis(point a,point b)
{
 return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
point findcenter(point p1,point p2)
{
 point p3,mid,center;
 double b,c,ang;
 p3.x=p2.x-p1.x;
 p3.y=p2.y-p1.y;
 mid.x=(p1.x+p2.x)/2;
 mid.y=(p1.y+p2.y)/2;
 b=dis(p1,mid);
 c=sqrt(1-b);
 if(fabs(p3.y)<eps)
 {
  center.x=mid.x;
  center.y=mid.y+c;
 }
 else
 {
  ang=atan(-p3.x/p3.y);
  center.x=mid.x+c*cos(ang);
  center.y=mid.y+c*sin(ang);
 }
 return center;
}
int main(){
 while((cin>>n)&&n!=0)
 {
  int i,j,k;
  int ans=1;
  for(i=0;i<n;i++)
   cin>>p[i].x>>p[i].y;
  for(i=0;i<n;i++)
  {
   int cnt;
   for(j=i+1;j<n;j++)
   {
    if(dis(p[i],p[j])<=4.0+eps)
    {
     cnt=0;
     point q=findcenter(p[i],p[j]);
     for(k=0;k<n;k++)
     {
      if(dis(q,p[k])<=1.0+eps) cnt++;
     }
     if(ans<cnt) ans=cnt;
    }
   }
  }
  cout<<ans<<endl;
 }
 return 0;
}