非线性规划的例题--飞行管理问题(1995年国赛A题)
目录
问题提出
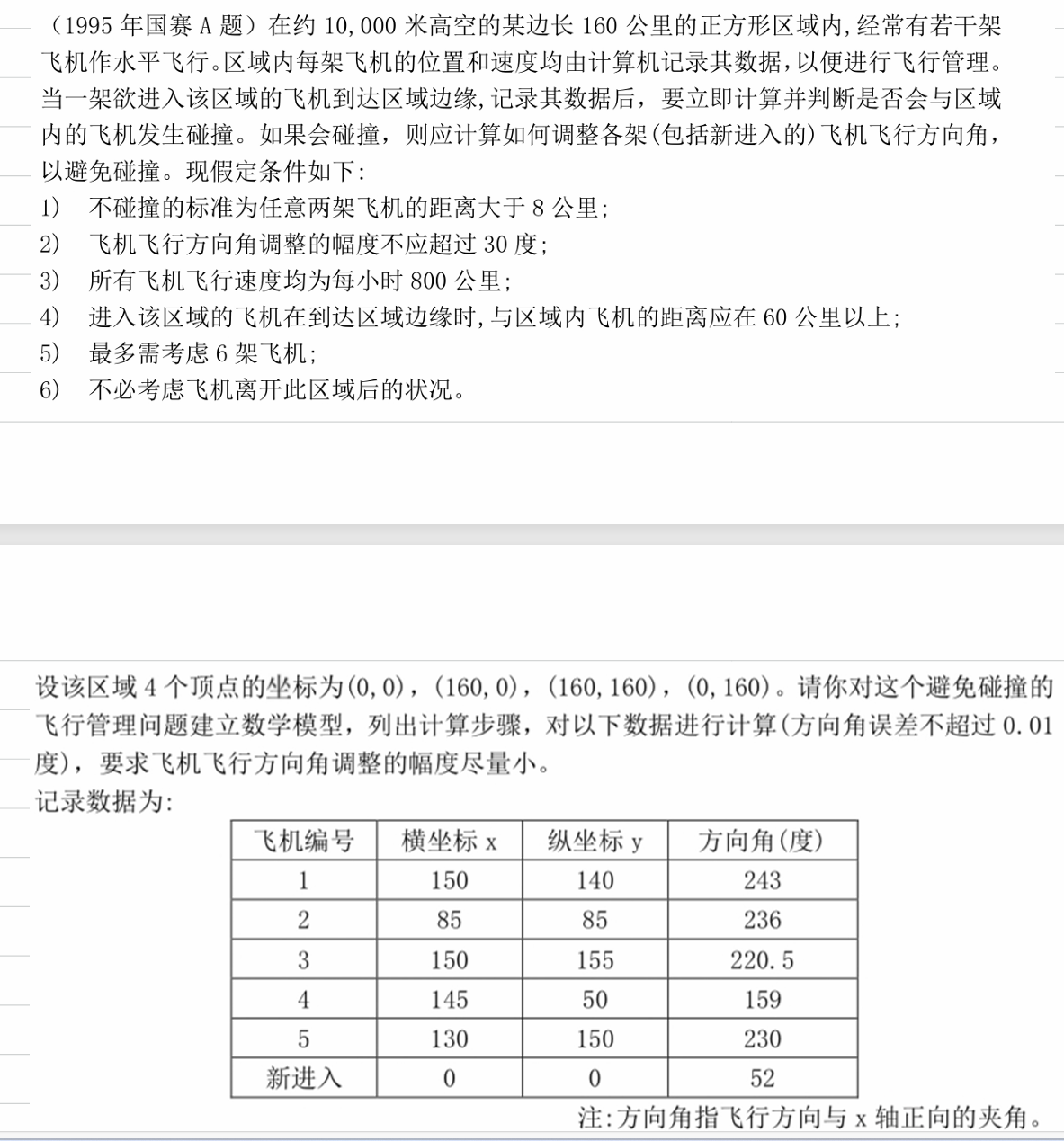
一、问题分析
本题要求在保证飞机不相撞的情况下,调整的角度最小,可以视作一个规划问题。保证在飞机之间最近的情况下,其距离仍然大于8km,使得调整角度的绝对值之和最小。难点在与求出在什么情况下,飞机之间的距离最小,是多少
二、模型假设
1.忽略飞机体积、转向时间等
2.早调整优于晚调整,第六架飞机刚进入区城时,所有飞机按照指示调整
在实际中,我们想要一步调整到位,因此选择第六架飞机进入区域后就马上进行调整,使整个过程一步到位
3.一次就调整到位,直到下一个飞机进入区域
三、模型建立
1.绘制平面图
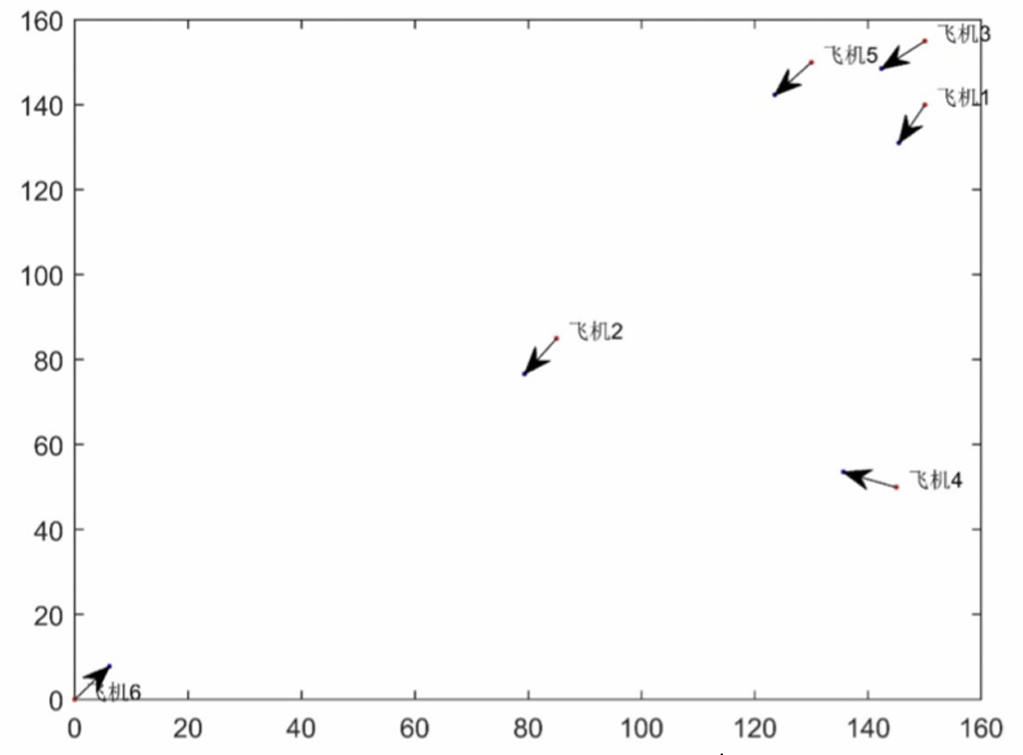
2.设置决策变量与目标函数
目标就是使得调整角度绝对值之和最小

3.建立约束
此处的约束有两个,一个为调整的角度的范围,从-30°到30°
另一个就是任意两架飞机距离的最小值不超过8km,而如何找到这个飞机距离的最小值是本题的关键和难点

4.求解约束--找到飞机距离的最小值
此约束的建立较为复杂,因此需要把约束解出来,一般的约束能直接写出来可跳过这一步

如何找出tij?首先我的想法是用数值模拟的方法,把时间t给离散化,依次给出距离,求最小,但是这种方法要求的算力比较大。下面我们来介绍利用函数的性质来求出tij的方法

我们把原本的dij写成一个函数,求出导数,进行分类讨论,利用极值点的性质来求出距离最小的时间点。
(1)df/dt>0
当f(x)的导数大于0时,说明这个距离会随时间的增大而增大,也就是说两架飞机的距离会越来越远,当t=0时,两架飞机的距离最近

(2)df/dt<0,之后>0
先<0后>0的情况下,两架飞机的距离逐渐接近,之后距离变远,也就是说,当df/dt=0的时,两架飞机的距离最近
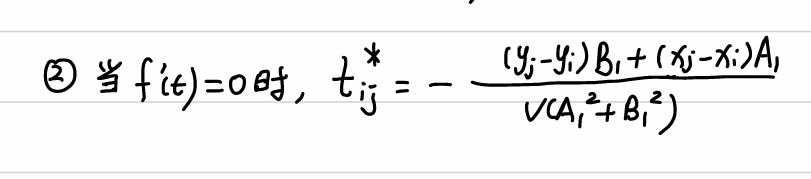
四、代码实现
1.变量初始化与绘图
format long g
clear;clc
figure(1) % 生成一个图形
box on % 显示为封闭的盒子
% 绘制飞机的初始位置
data = [150 140 243;
85 85 236;
150 155 220.5;
145 50 159;
130 150 230;
0 0 52];
plot(data(:,1),data(:,2),'.r')
axis([0 160,0,160]);% 设置坐标轴刻度范围
hold on;
% 在图上标上注释
for i = 1:6
txt = ['飞机',num2str(i)];
text(data(i,1)+2,data(i,2)+2,txt,'FontSize',8)
end
% 把Matlab做出来的图可以导出,然后再放到PPT中画出飞机飞行方向的箭头(就和讲义上的类似)
2.输入非线性约束
此代码有虽然是数值计算,但其有比较好的编程思想值得学习
(1)生成co与si的向量,用循环求出距离矩阵。
(2)距离矩阵使用先从2:n进行循环,再进行1:i-1循环,避免了重复计算
function [c,ceq] = nonlfun6(delta) % 决策变量delta为六架飞机调整的角度
x = [150 85 150 145 130 0]; % 飞机初始位置的横坐标
y = [140 85 155 50 150 0]; % 飞机初始位置的纵坐标
theta = [243 236 220.5 159 230 52] * pi / 180; % 飞机初始的飞行方向角
v = 800; % 飞机速度
co = cos(theta + delta); % 包含6个元素的向量
si = sin(theta + delta); % 包含6个元素的向量
% 下面开始计算飞机i和j之间的最短距离(只需要计算矩阵的一半即可)
d = zeros(6); % 初始化飞机两两之间的最短距离矩阵
for i = 2: 6
for j = 1: i-1
% 套用我们推导出来的公式计算飞机i和飞机j相距最近的时间
fenzi = ((y(j)-y(i))*(si(j)-si(i)) +(x(j)-x(i))*(co(j)-co(i))) ; % 分子
fenmu = v * ((co(j)-co(i))^2 + (si(j)-si(i))^2); % 分母
t(i,j) =- fenzi / fenmu;
if t(i,j) <0
d(i, j) = 1000; % 此时最初的位置就是相距最近的点,因为最初的时候所有飞机两两之间的距离就大于8,因此未来绝不会相撞,我们令它们的距离为一个特别大的数
else
d(i, j) = sqrt((x(j)-x(i)+v*t(i,j)*(co(j)-co(i)))^2+(y(j)-y(i)+v*t(i,j)*(si(j)-si(i)))^2);
end
end
end
% 非线性不等式约束
c =ones(15,1)*8.000001 - [d(2,1); d(3,1:2)'; d(4,1:3)'; d(5,1:4)'; d(6,1:5)'];
% 12个非线性不等式约束: “最短距离>8” 等价于 “8 - 最短距离<0”
% 注意: 由于Matlab标准型中取的是小于等于号,因此这里取一个比8略大的数:8.000001-最短距离<=0
ceq = []; % 没有非线性等式约束
end
3.进行求解
x0 = [0 0 0 0 0 0]; % 初始值
lb = -pi/6*ones(6,1);
ub = pi/6*ones(6,1);
[x,fval] = fmincon(@fun6,x0,[],[],[],[],lb,ub,@nonlfun6)
x = x * 180 / pi



 浙公网安备 33010602011771号
浙公网安备 33010602011771号