后缀自动机学习小记

一、$SAM$ 的性质

$SAM$ 是个状态机。一个起点，若干终点。原串的所有子串和从 $SAM$ 起点开始的所有路径一一对应，不重不漏。所以终点就是包含后缀的点。
每个点包含若干子串，每个子串都一一对应一条从起点到该点的路径。且这些子串一定是里面最长子串的连续后缀。
$SAM$ 问题中经常考虑两种边：
- 普通边，类似于 $Trie$。表示在某个状态所表示的所有子串的后面添加一个字符。
- $Link$、$Father$。表示将某个状态所表示的最短子串的首字母删除。这类边构成一棵树。

二、$SAM$ 的构造思路

$endpos(s)$：子串 $s$ 所有出现的位置（尾字母下标）集合。$SAM$ 中的每个状态都一一对应一个 $endpos$ 的等价类。
$endpos$ 的性质：
- 令 $s1$,$s2$ 为 $S$ 的两个子串，不妨设 $|s1| \le |s2|$ （我们用 $|s|$ 表示 $s$ 的长度，此处等价于 $s1$ 不长于 $s2$）。则 $s1$ 是 $s2$ 的后缀当且仅当 $endpos(s1) \supseteq endpos(s2)$ ，$s1$ 不是 $s2$ 的后缀当且仅当 $endpos(s1) \cap endpos(s2) = \emptyset$　。
- 两个不同子串的 $endpos$，要么有包含关系，要么没有交集。
- 两个子串的 $endpos$ 相同，那么短串为长串的后缀。
- 对于一个状态 $st$，以及任意的 $longest(st)$ 的后缀 $s$，如果 $s$ 的长度满足：$|shortest(st)| \le |s| \le |longsest(st)|$ ，那么 $s \in substrings(st)$。

三、$SAM$ 的构造过程

对于字符串 $S = \texttt{aabbabd}$，它的后缀自动机是：

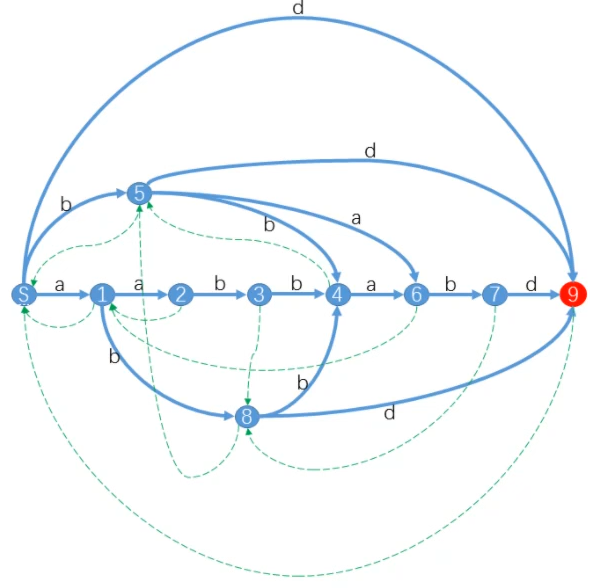
这里蓝色的边是后缀自动机的普通边，而绿边则是上面说的 $Father$ 边。

$SAM$ 采用逐个添加字符的方式构造。

inline void extend(int c){
    int p = last, np = last = ++ tot;
    ct[np] = 1, tr[np].len = tr[p].len + 1;

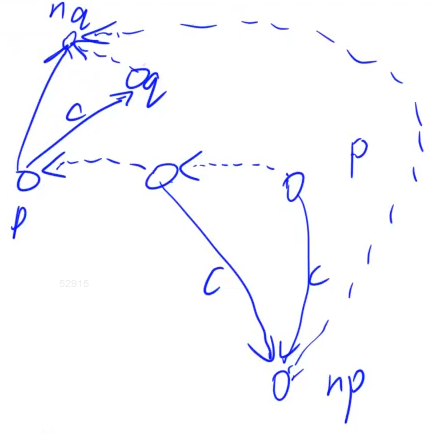
这里 $p$ 表示当前串的最长前缀（整个当前串，称之为旧串）所在状态（$endpos$ 等价类）对应的点，$np$ 则是添加 $c$ 后新串的最长前缀所在状态对应的点。$ct$ 数组用来记录当前状态包含的子串个数。

while(p && !tr[p].son[c]) tr[p].son[c] = np, p = tr[p].fa;

首先从 $p$ 开始沿着绿边一直跳，经过的每一个点如果没有 $c$ 这条边则连一条 $c$ 的边到 $np$，否则停下。

if(!p) tr[np].fa = 1;

这里判断一下，如果全都没有 $c$ 这条边，那么就将 $np$ 的绿边连到起点上，否则进行下一步：

if(tr[q].len == tr[p].len + 1) tr[np].fa = q;

设第一个找到的有 $c$ 这条边的点 $c$ 边指向 $q$。判断 $q$ 的长度是否为 $p$ 的长度 $ + 1$，若是则将 $np$ 的绿边连到 $q$ 上。

else{
    int nq = ++ tot; tr[nq] = tr[q];
    tr[nq].len = tr[p].len + 1;
    tr[q].fa = tr[np].fa = nq;
    while(p && tr[p].son[c] == q) tr[p].son[c] = nq, p = tr[p].fa;
}

否则新建一个点 $nq$，继承 $q$ 的信息，并像链表一样插到 $q$ 和 $q$ 绿边连向的点中间。然后将 $nq$ 的长度设为 $p$ 的长度 $ + 1$。将 $np$ 的绿边连到 $nq$ 上，继续沿着绿边跳 $p$，将所有绿边连向 $q$ 的点的绿边转移到 $nq$ 上。

关于求每个状态包含串的出现个数（也就是 $endpos$ 集合中位置的个数）。以绿边建一棵树，被指向的点是父亲，不难发现，几个儿子是父亲的 $endpos$ 集合的划分，却并不一定划分完，有且仅有原串前缀对应的点会多出一个，所以在构造后缀自动机时先将前缀对应的点的个数（也就是 $ct$）$ + 1$，然后父亲的个数为儿子个数总和加上自己本身个数即可。

四、$SAM$ 时间复杂度

线性。
证明较为复杂，略。

模板题：洛谷 P3804 【模板】后缀自动机（SAM）

题目大意：

给定一个只包含小写字母的字符串 $S$。
请你求出 $S$ 的所有出现次数不为 $1$ 的子串的出现次数乘上该子串长度的最大值。

代码实现：

#include <bits/stdc++.h>
inline int read(){
    int s = 0, f = 0; char ch = getchar();
    while(!isdigit(ch)){if(ch == '-') f = 1; ch = getchar();}
    while(isdigit(ch)) s = s * 10 + ch - 48, ch = getchar();
    return f ? ~s + 1 : s;
}
inline int max(int x, int y){return x > y ? x : y;}
inline int min(int x, int y){return x < y ? x : y;}
const int N = 1e6 + 5;
struct node{
    int len, fa;
    int son[26];
}tr[N << 1];
char s[N];
int n, last = 1, tot = 1;
int ct[N << 1], ans;
int head[N << 1], ne[N << 1], to[N << 1], idx;
inline void add(int u, int v){
    to[++ idx] = v, ne[idx] = head[u], head[u] = idx;
    return;
}
inline void extend(int c){
    int p = last, np = last = ++ tot;
    ct[np] = 1, tr[np].len = tr[p].len + 1;
    while(p && !tr[p].son[c]) tr[p].son[c] = np, p = tr[p].fa;
    if(!p) tr[np].fa = 1;
    else{
        int q = tr[p].son[c];
        if(tr[q].len == tr[p].len + 1) tr[np].fa = q;
        else{
            int nq = ++ tot; tr[nq] = tr[q];
            tr[nq].len = tr[p].len + 1;
            tr[q].fa = tr[np].fa = nq;
            while(p && tr[p].son[c] == q) tr[p].son[c] = nq, p = tr[p].fa;
        }
    }
    return;
}
void dfs(int u){
    for(int i = head[u]; i; i = ne[i]){ 
        dfs(to[i]);
        ct[u] += ct[to[i]];
    }
    if(ct[u] > 1) ans = max(ans, ct[u] * tr[u].len);
    return;
}
int main(){
    scanf("%s", s);
    n = strlen(s);
    for(int i = 0; i < n; ++ i) extend(s[i] - 'a');
    for(int i = 2; i <= tot; ++ i) add(tr[i].fa, i);
    dfs(1);
    printf("%d\n", ans);
    return 0;
}

posted @ 2023-05-11 17:00 牛肉爱吃dks 阅读(49) 评论(0) 收藏举报

刷新页面返回顶部

牛肉爱吃dks

后缀自动机学习小记

一、\(SAM\) 的性质

二、\(SAM\) 的构造思路

三、\(SAM\) 的构造过程

四、\(SAM\) 时间复杂度

模板题：洛谷 P3804 【模板】后缀自动机（SAM）

题目大意：

代码实现：

公告