后缀数组学习小记

模板题：acwing 2715.后缀数组

题目大意：

给定一个长度为 \(n\) 的字符串 \(S\)，求出 \(SA\) 数组和 \(Height\) 数组。
定义从第 \(i\) 个字符开始的后缀编号为 \(i\)。
\(SA_i\) 表示排名第i的后缀编号。
\(Height_i\) 表示排名为 \(i\) 的非空后缀与排名为 \(i − 1\) 的非空后缀的最长公共前缀的长度
特别地：规定 \(Height_1 = 0\)

算法流程：

求 \(SA\) 数组有两种方法，一种是倍增法，\(O(n\log_2 n)\) 的时间复杂度，一种是DC3，\(O(n)\) 的时间复杂度，但常数很大且较复杂。所以常用倍增法。

首先要求 \(SA\) 数组：

\(\texttt{step}\;1\)
将所有后缀按照第一个字符基数排序，相同的保留原有顺序不变，求出当前的 \(SA\) 数组。

\(\texttt{step}\;2\)
假设当前已经按前 \(k\) 个字符排好序，将前 \(k\) 个字符当成第一关键字，第 \(k + 1\) 至 \(2k\) 个字符当成第二关键字排序。
显然，第 \(i\) 个后缀的第二关键字就是第 \(i + k\) 个后缀的第一关键字。

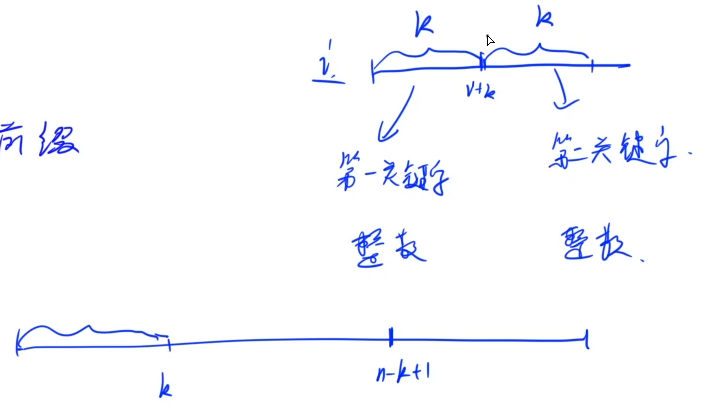
为了满足基数排序条件，可以先将其按第二关键字排序，再按第一关键字基数排序。
\(k\) 从 \(1\) 开始，每次翻倍。

然后求 \(Height\) 数组：
设 \(rk_i\) 表示第 \(i\) 个后缀的排名。

引理1
设 \(lcp(i, j)\) 表示第 \(SA_i\) 个后缀和第 \(SA_j\) 个后缀的最长公共前缀长度，当 \(i < j < k\) 时 \(lcp(i, j) = \min(lcp(i, k), lcp(k, j))\)。

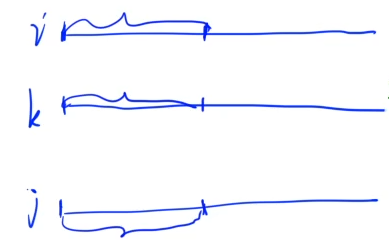
引理2
设 \(h_i=Height_{rk_i}\)，则有 \(h_i \ge h_{i - 1} - 1\)。

证明：
设 \(SA_{rk_i - 1} = k\)，故 \(h_{i - 1} = lcp(i - 1, k)\)。
若 \(S_{i - 1} \ne S_k\)，则 \(h_{i - 1} = 0\)，故 \(h_i \ge h_{i - 1} - 1 = 0\)。
否则，\(lcp(rk_i, rk_{k + 1}) = h_{i - 1} - 1\) 且 \(rk_{k + 1} \le rk_{sa_i - 1} < rk_i\)。由引理1得，\(lcp(rk_i, rk_{k + 1}) = \min(lcp(rk_i, rk_{sa_i - 1}), lcp(rk_{sa_i - 1}, rk_{k + 1}))\) 故 \(h_i = lcp(rk_i, rk_{sa_i - 1}) \ge lcp(rk_i, rk_{k + 1}) = h_{i - 1} - 1\)。

根据引理2，求 \(Height_i\) 时可以从 \(Height_{rk_{i - 1}} - 1\) 开始比对，时间复杂度 \(O(n)\)。

代码实现：

#include <bits/stdc++.h>
inline int read(){
    int s = 0, f = 0; char ch = getchar();
    while(!isdigit(ch)){if(ch == '-') f = 1; ch = getchar();}
    while(isdigit(ch)) s = s * 10 + ch - 48, ch = getchar();
    return f ? ~s + 1 : s;
}
inline int max(int x, int y){return x > y ? x : y;}
inline int min(int x, int y){return x < y ? x : y;}
const int N = 1e6 + 5;
int n, m;
int sa[N], rk[N], c[N];                                                                                 //sa[i]:排名第i的后缀 rk[i]:第i个后缀的排名
int x[N], y[N];                                                                                         //x[i]:第i个后缀的的第一关键字 y[i]:按第二关键字排序后排名为i的后缀编号
int height[N];
char s[N];
inline int num(char ch){                                                                                //字母转数字，相对顺序不变
    if(isdigit(ch)) return ch - '0' + 1;
    else if(isupper(ch)) return ch - 'A' + 11;
    else return ch - 'a' + 37;
}
inline void get_sa(){
    for(int i = 1; i <= n; ++ i) ++ c[x[i] = num(s[i])];
    for(int i = 2; i <= m; ++ i) c[i] += c[i - 1];
    for(int i = n; i; -- i) sa[c[x[i]] --] = i;                                                         //基数排序，按第一个字符                                                                                                    
    for(int k = 1; k <= n; k <<= 1){                                                                    //k表示第一关键字和第二关键字的长度
        int cnt = 0;
        for(int i = n - k + 1; i <= n; ++ i) y[++ cnt] = i;                                             //后k个后缀第二关键字为0
        for(int i = 1; i <= n; ++ i)
            if(sa[i] > k) y[++ cnt] = sa[i] - k;                                                        //第i-k个后缀的第二关键字为第i个后缀的第一关键字
        for(int i = 1; i <= m; ++ i) c[i] = 0;
        for(int i = 1; i <= n; ++ i) ++ c[x[i]];
        for(int i = 2; i <= m; ++ i) c[i] += c[i - 1];
        for(int i = n; i; -- i) sa[c[x[y[i]]] --] = y[i];                                               //再按第一关键字排序
        std::swap(x, y);                                                                                //便于第一关键字x更新
        x[sa[1]] = cnt = 1;
        for(int i = 2; i <= n; ++ i)
            x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? cnt : ++ cnt;   //更新第一关键字
        if(cnt == n) break;                                                                             //已经两两不同就结束
        m = cnt;                                                                                        //不同第一关键字的个数
    }
    for(int i = 1; i <= n; ++ i) rk[sa[i]] = i;
    return;
}
inline void get_height(){
    for(int i = 1, k = 0; i <= n; ++ i){
        if(rk[i] == 1) continue;
        if(k) -- k;
        int j = sa[rk[i] - 1];                                                                          //排名在第i个后缀之前一个的后缀编号
        while(i + k <= n && j + k <= n && s[i + k] == s[j + k]) ++ k;
        height[rk[i]] = k;
    }
    return;
}
int main(){
    scanf("%s", s + 1);
    n = strlen(s + 1), m = 62;
    get_sa();
    get_height();
    for(int i = 1; i <= n; ++ i) printf("%d ", sa[i]);
    puts("");
    for(int i = 1; i <= n; ++ i) printf("%d ", height[i]);
    return 0;
}