pyTorch基础

什么是动量：

在物理学中：动量（Momentum），又称线动量，是物理学中刻画物体运动状态的核心矢量。它定义为物体质量与速度的乘积，表达式为p=mv 。在国际单位制中，动量的单位是千克·米每秒（kg·m/s）。

机器学习中：动量（Momentum）方法通过累积之前梯度的方向来加速梯度下降，使得优化过程更加稳定，并且有助于跳出局部极小值。

核心思想：

加速下降：在梯度一致的方向上，动量累积后能够加速下降，提高收敛速度。

降低震荡：在高噪声或曲率大的方向上（如鞍点附近），动量可以降低震荡，提高优化稳定性。

跨越局部极小值：由于动量累积了之前的梯度信息，在遇到局部极小值时仍然可能继续前进，从而避免陷入局部极小值。
什么是鞍点：数学含义是： 目标函数在此点上的梯度（一阶导数）值为 0

 当处于鞍点位置时，由于当前的梯度为 0，参数无法更新。但是 Momentum 动量梯度下降算法已经在先前积累了一些梯度值，很有可能使得跨过鞍点。

由于 mini-batch 普通的梯度下降算法，每次选取少数的样本梯度确定前进方向，可能会出现震荡，使得训练时间变长。Momentum 使用移动加权平均，平滑了梯度的变化，使得前进方向更加平缓，有利于加快训练过程。

正则化

在设计机器学习算法时希望在新样本上的泛化能力强。许多机器学习算法都采用相关的策略来减小测试误差，这些策略被统称为正则化。

神经网络的强大的表示能力经常遇到过拟合，所以需要使用不同形式的正则化策略。

过拟合：是指模型因参数过多而过度适应训练数据，导致泛化能力下降的现象。这种情况下模型可能只是记住了训练集数据，而不是学习到了数据特征。

欠拟合：模型描述能力太弱，以至于不能很好地学习到数据中的规律。产生欠拟合的原因通常是模型过于简单。

目前在深度学习中使用较多的策略有范数惩罚，DropOut，特殊的网络层等

 

Dropout（随机失活）正则化

在训练过程中，Dropout的实现是让神经元以超参数p（入参，eg：dropout = nn.Dropout(p=0.4)，随机失活概率是0.4）的概率停止工作或者激活被置为0,未被置为0的进行缩放，缩放比例为1/(1-p)。

在测试过程中，随机失活不起作用。

 

批量归一化(BN层)

 先对数据标准化，再对数据重构（缩放+平移）

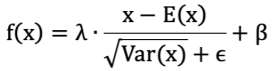
　　λ 和 β 是可学习的参数，它相当于对标准化后的值做了一个线性变换，λ 为系数，β 为偏置；
　　eps 通常指为 1e-5，避免分母为 0；
　　E(x) 表示变量的均值；
　　Var(x) 表示变量的方差；
批量归一化层在计算机视觉领域使用较多

 logits

Logits 是深度学习模型预测过程中最后一层输出的原始值。它们通常是一个未归一化的实数向量，每个值对应一个类别。Logits 的取值范围可以是正数、负数，甚至非常大或非常小的值。

Logits 是模型预测的中间结果。它们本身并非最终的预测值，而需要通过激活函数（如 Softmax）进行归一化，转化为概率分布。模型的优化目标（如交叉熵损失）直接基于 Logits 或其归一化结果进行计算。

criterion = nn.CrossEntropyLoss()  #适用于多类别分类问题

 

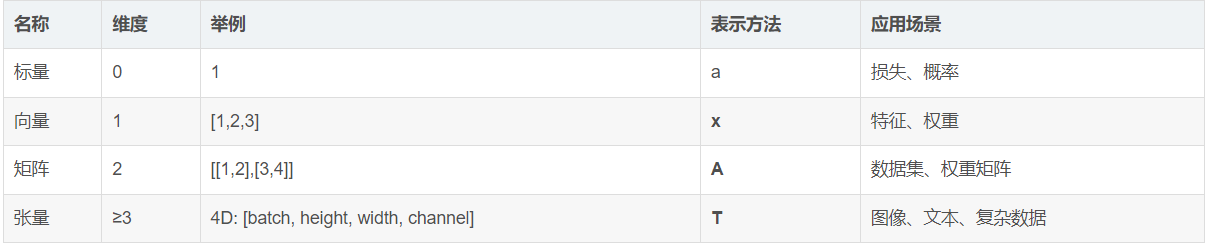
什么是标量，向量，矩阵，张量：

标量：标量就是一个单独的数值。它没有方向，只有大小。

向量（Vector）：向量是一组有序的数值，可以理解为一维数组。它有大小和方向。

矩阵（Matrix）：矩阵是一个二维数组，由多个向量组成。可以理解为表格。

张量（Tensor）：张量是更高维度的数组，标量是一阶张量，向量是二阶，矩阵是三阶，更多维度就是更高阶的张量。

 

在PyCharm中，张量(Tensor)是PyTorch框架的核心数据结构，本质是多维数组，用于存储和操作数值数据。以下是关键点：

张量的基本概念

• 定义：张量只有一种类型，如果是int型，则张量中所有数据都为int型，并且维度可以是0维，1维，2维，3维等等...，支持任意维度的数值存储 。

张量的基本类型：

（确认张量是几维：0维没有[]，几维就有几个[]） 

0维张量：标量(scalar)

scalar = torch.tensor(7)
scalar.ndim

输出：>>> 0

1维张量：向量(vector)

vector = torch.tensor([7, 7])
vector.ndim

输出：>>> 1

2维张量：矩阵(matrix)

MATRIX = torch.tensor([[7, 8],
[9, 10]])
MATRIX.ndim

输出：>>> 2

多维张量

TENSOR = torch.tensor([[[1, 2, 3],
[3, 6, 9],
[2, 4, 5]]])
TENSOR.ndim

输出：>>> 3

说明：

torch.tensor根据指定数据创建张量

import torch # 需要安装torch模块,虚拟环境中已经安装好了
import numpy as np
# 1. 创建张量标量
data = torch.tensor(10)
print(data)
# 2. numpy 数组, 由于 data 为 float64, 下面代码也使用该类型
data = np.random.randn(2, 3)
data = torch.tensor(data)

print(data)
# 3. 列表, 下面代码使用默认元素类型 float32
data = [[10., 20., 30.], [40., 50., 60.]]
data = torch.tensor(data)

#--------------------------------------------

输出结果:
tensor(10)
tensor([[ 0.1345, 0.1149, 0.2435],
[ 0.8026, -0.6744, -1.0918]], dtype=torch.float64)
tensor([[10., 20., 30.],
[40., 50., 60.]])

torch.Tensor根据形状创建张量, 其也可用来创建指定数据的张量

# 1. 创建2行3列的张量, 默认 dtype 为 float32
data = torch.Tensor(2, 3)
print(data)
# 2. 注意: 如果传递列表, 则创建包含指定元素的张量
data = torch.Tensor([10])
print(data)
data = torch.Tensor([10, 20])
print(data)

#----------------------------------------------------------
输出结果:
tensor([[0.0000e+00, 3.6893e+19, 2.2018e+05],
[4.6577e-10, 2.4158e-12, 1.1625e+33]])
tensor([10.])
tensor([10., 20.])

torch.IntTensor、torch.FloatTensor、torch.DoubleTensor创建指定类型的张量

• 直接创建方法：
  • torch.IntTensor()：创建int32类型张量
  • torch.FloatTensor()：创建float32类型张量
  • torch.DoubleTensor()：创建float64类型张量
• 注意事项：
  • 当传入元素类型不正确时会自动进行类型转换
  • 示例：torch.IntTensor([2.5, 3.3])会将浮点数强制转换为整数

类型转换的区别

• 两种转换方式：
  • data.type(torch.DoubleTensor)：通过指定目标类型转换
  • data.double()：直接调用类型方法转换
• 存储格式说明：
  • torch.float64表示数值的存储格式
  • torch.DoubleTensor表示创建的是float64格式的张量对象
• 实际应用建议：
  • 推荐使用torch.DoubleTensor创建张量
  • 数值转换后dtype显示的是存储格式而非对象类型

特殊张量创建

• 全1张量：
  • torch.ones()：创建指定形状的全1张量
  • torch.ones_like()：根据已有张量形状创建全1张量
• 全0张量：
  • torch.zeros()：创建指定形状的全0张量
  • torch.zeros_like()：根据已有张量形状创建全0张量
• 指定值张量：
  • torch.full()：创建指定形状和值的张量
  • torch.full_like()：根据已有张量形状创建指定值张量
  • 示例：torch.full([2,3], 10)创建2行3列全为10的张量

线性张量创建 

• torch.arange()：
  • 在指定区间按步长生成元素（左闭右开区间）
  • 示例：torch.arange(0, 10, 2) → tensor([0, 2, 4, 6, 8])      参数第三位含义：隔两步取一个值
• torch.linspace()：
  • 在指定区间按元素个数均匀生成（闭区间）
  • 示例：torch.linspace(0, 11, 10) → tensor([0.0000,1.2222,...,11.0000])    参数第三位含义：一共取十个值

• 关键区别：
  • arange通过步长控制，linspace通过元素数量控制
  • arange是左闭右开，linspace是闭区间

指定值张量：
torch.full()
torch.full_like()
_like方法说明：后缀_like表示创建与输入张量形状相同的新张量  ；只关注输入张量的形状，不关心具体数值

张量类型转换

• 转换方法：
  • data.type(torch.DoubleTensor)
  • data.double()
• 注意事项：
  • 类型转换会创建新的张量对象
  • 需要根据计算需求选择合适的数值精度

随机张量创建

1）随机数生成

• 随机种子设置：
  • torch.random.initial_seed()
  • torch.random.manual_seed()
• 正态分布随机数：
  • torch.randn()：生成标准正态分布的随机张量

矩阵乘法

torch.matmu：广义的矩阵乘法（适用于任意维度张量）

torch.matmul()函数提供了更广泛的矩阵乘法功能，它可以处理任意维度的张量。这个函数会按照张量的维度自动进行合适的乘法操作。

torch.mm()：矩阵乘法（只适用于二维张量）

torch.mm()函数用于执行矩阵乘法，但它只适用于二维张量（即矩阵）。如果你试图对高于二维的张量使用torch.mm()，将会得到一个错误。

torch.mul()：元素级别的乘法

torch.mul()函数用于执行元素级别的乘法，即对应位置的元素相乘。这个函数对于两个形状相同的张量特别有用。

import torch

# 创建两个二维张量
matrix1 = torch.tensor([[1, 2], [3, 4]])
matrix2 = torch.tensor([[5, 6], [7, 8]])

# 使用torch.mm()进行矩阵乘法
result_mm = torch.mm(matrix1, matrix2)
print(result_mm)

# 对于二维张量，torch.matmul()与torch.mm()行为相同
result_matmul_2d = torch.matmul(matrix1, matrix2)
print(result_matmul_2d)

# 对于高于二维的张量，torch.matmul()可以执行广播和批量矩阵乘法
tensor3d_1 = torch.randn(3, 2, 4)  # 3个2x4的矩阵
tensor3d_2 = torch.randn(3, 4, 5)  # 3个4x5的矩阵

# 批量矩阵乘法
result_matmul_3d = torch.matmul(tensor3d_1, tensor3d_2)
print(result_matmul_3d.shape)  # 输出应为(3, 2, 5)，表示3个2x5的矩阵

张量与NumPy数组转换

基本方法：使用Tensor.numpy()函数转换，但会共享内存　　

 内存问题：共享内存意味着修改原张量会影响转换后的NumPy数组，反之亦然

　　　　　　通过.copy()函数可避免共享内存问题

data_tensor = torch.tensor([2, 3, 4])
data_numpy = data_tensor.numpy()  # 共享内存
data_numpy_copy = data_tensor.numpy().copy()  # 不共享内存

使用 torch.tensor可以将ndarray数组转换为Tensor，默认不共享内存。

• • 张量→NumPy：
    • .numpy()共享内存
    • .numpy().copy()不共享内存
  • NumPy→张量：
    • from_numpy()共享内存
    • tensor()不共享内存

• • 标量处理：
    • 零维张量用.item()获取数值
    • 单元素张量同样适用

张量基本运算:

　　包括加减乘除（add/sub/mul/div）和取负（neg）五种基础运算

• • 带下划线版本：如add_、sub_等会直接修改原数据，等价于+=操作
  • 标准版本：如add()会返回新张量，原数据保持不变

点乘运算

点乘指（Hadamard）的是两个同维矩阵对应位置的元素相乘，使用mul 和运算符 * 实现。

矩阵乘法运算

矩阵乘法运算要求第一个矩阵 shape: (n, m)，第二个矩阵 shape: (m, p), 两个矩阵点积运算 shape 为: (n, p)。

 

3. 点积运算：

• 运算符@用于进行两个矩阵的点乘运算

• torch.matmul 对进行点乘运算的两矩阵形状没有限定，对数输入的 shape 不同的张量, 对应的最后几个维度必须符合矩阵运算规则

常见运算函数

均值计算:数据类型要求：必须为Float或Double类型张量才能计算均值

全局均值：data.mean()计算所有元素的平均值

维度指定：dim=0按列计算，dim=1按行计算

维度指定方法

维度记忆：dim=0表示列操作，dim=1表示行操作；类比理解：类似图像坐标系，编程中行列编号常与数学习惯相反；应用场景：求和(sum)、均值(mean)等统计函数均可指定维度

示例验证：对上述张量按行求和得[11,14]，按列求和得[10,3,12]

指数对数运算

平方根：data.sqrt()计算每个元素的平方根；指数运算：data.exp()计算每个元素的自然指数 e^x

对数运算：data.log()：以e为底的自然对数；data.log2()：以2为底的对数；data.log10()：以10为底的对数

幂运算：torch.pow(data, n)计算data的n次方，如平方用2，立方用3

核心函数：sum(求和)、mean(均值)、sqrt(平方根)、pow(幂次)、exp(指数)、log(对数)

记忆技巧：统计类(sum/mean)、代数类(sqrt/pow)、高等数学类(exp/log)

张量索引操作

基本原则：数字从零开始：所有索引计数从0开始，如第0行、第0列；冒号表示全部：data[:,0]表示取所有行的第0列；单值取行：data[0]表示取第0行所有元素；双值取行列：data[行,列]格式，左边是行索引，右边是列索引

 data[0] → tensor([0,7,6,5,9])（取第0行）；data[:,0] → tensor([0,6,6,4])（取所有行的第0列）

列表索引

两种形式：对应位置取值：data[[0,1],[1,2]] → 取(0,1)和(1,2)位置的元素（7和3）；范围取值：data[[[0],[1]],[1,2]] → 取第0行和第1行的1-2列（[[7,6],[8,3]]）

关键区别：第一种形式取的是离散的单个元素；第二种形式取的是连续的行列范围组合

 范围索引原则

左闭右开原则：data[:3,:2] → 取0-2行（不含第3行），0-1列（不含第2列）；data[2:,:2] → 从第2行到最后，取前两列

实际应用：冒号前数字包含，冒号后数字不包含；如data[1:3]取第1、2行（不含第3行）

 布尔索引

两种形式：单条件筛选：data[data[:,2]>5] → 筛选第2列值>5的所有行；多条件筛选：data[:,data[1]>5] → 筛选第1行值>5的所有列

reshape函数

 功能：在不改变张量数据前提下改变维度形状；可直接获取形状：data.shape或data.size()；支持任意合法形状变换：内存连续性：不要求数据存储在连续内存块

import torch
data = torch.tensor([[10, 20, 30], [40, 50, 60]])
# 1. 使用 shape 属性或者 size 方法都可以获得张量的形状
print(data.shape, data.shape[0], data.shape[1])
print(data.size(), data.size(0), data.size(1))
# 2. 使用 reshape 函数修改张量形状
new_data = data.reshape(1, 6)
print(new_data.shape)
'''
输出结果:
torch.Size([2, 3]) 2 3
torch.Size([2, 3]) 2 3
torch.Size([1, 6])
'''

squeeze和unsqueeze函数 

squeeze：功能：删除形状为1的维度（降维）；示例：tensor([ [1],[2],[3] ]).squeeze() → tensor([1,2,3])

unsqueeze：功能：添加形状为1的维度（升维）;维度参数：dim=0：在最前面添加维度；dim=1：在中间添加维度；dim=-1：在最后添加维度；应用场景：图像处理中增加batch维度

transpose和permute函数

transpose：功能：交换两个指定维度；限制：每次只能交换两个维度

permute：　功能：一次性重排多个维度顺序；优势：比多次transpose更高效；内存影响：操作后数据可能变为非连续存储

view和contiguous函数

view函数：

　　参数乘积必须等于原张量元素总数‌：这是使用view方法的基本前提

　　功能：修改张量形状（类似reshape）；限制：要求数据存储在连续内存块；不适用场景：transpose/permute后的张量；

torch.view 方法的参数数量是‌可变的‌，你可以根据需要传入任意多个参数。每个参数都代表张量在对应维度上的大小。

‌参数的具体含义：‌

• ‌每个参数都是整数‌，对应新张量在该维度的大小
• ‌参数-1的特殊作用‌：表示该维度由PyTorch自动计算，保证总元素数不变
  
• ‌参数乘积必须等于原张量元素总数‌：这是使用view方法的基本前提

‌实际应用示例：‌

• x.view(3, 2)：将张量重构成3行2列1
• x.view(-1)：将张量展平为一维1
• x.view(-1, 2)：自动计算行数，确保有2列1：

contiguous函数：作用：将非连续存储张量转为连续存储；判断连续性：组合使用：通过is_contiguous()方法检测

# 1 一个张量经过了 transpose 或者 permute 函数的处理之后，就无法使用
view 函数进行形状操作
# 若要使用view函数, 需要使用contiguous() 变成连续以后再使用view函数
# 2 判断张量是否使用整块内存
data = torch.tensor( [[10, 20, 30],[40, 50, 60]])
print('data--->', data, data.shape)
# 1 判断是否使用整块内存
print(data.is_contiguous()) # True
# 2 view
mydata2 = data.view(3, 2)
print('mydata2--->', mydata2, mydata2.shape)
# 3 判断是否使用整块
print('mydata2.is_contiguous()--->', mydata2.is_contiguous())

'''
输出结果:
data---> tensor([[10, 20, 30],
[40, 50, 60]]) torch.Size([2, 3])
True
mydata2---> tensor([[10, 20],
[30, 40],
[50, 60]]) torch.Size([3, 2])
mydata2.is_contiguous()---> True
'''

x = torch.arange(6)
print("x->", x)
z = x.view(2, 3)
print("z->", z)
# 使用 reshape 改变形状为 (3, 2)
y = torch.reshape(x, (3, 2))
print("y->", y)
print(y)

'''

x-> tensor([0, 1, 2, 3, 4, 5])
z-> tensor([[0, 1, 2],
[3, 4, 5]])
y-> tensor([[0, 1],
[2, 3],
[4, 5]])
tensor([[0, 1],
[2, 3],
[4, 5]])

'''

张量拼接操作

cat函数使用

基本功能：torch.cat()函数可以将两个张量根据指定的维度拼接起来，不改变维度数。

维度原则：遵循从零开始编号和左闭右开两个基本原则。

• 拼接示例：
  • 原始张量：三维张量（1通道×2行×3列）
  • dim=0拼接：将两个1通道张量拼接成2通道，结果尺寸为2×2×3
  • dim=1拼接：按行拼接，将两行扩展为四行，结果尺寸为1×4×3
  • dim=2拼接：按列拼接，将三列扩展为六列，结果尺寸为1×2×6
• 实际应用：在模型训练中需要明确每个维度的拼接方式，理解拼接后的张量形状变化。

import torch
data1 = torch.randint(0, 10, [1, 2, 3])
data2 = torch.randint(0, 10, [1, 2, 3])
print(data1)
print(data2)
# 1. 按0维度拼接
new_data = torch.cat([data1, data2], dim=0)
print(new_data)
print(new_data.shape)
# 2. 按1维度拼接
new_data = torch.cat([data1, data2], dim=1)
print(new_data)
print(new_data.shape)
# 3. 按2维度拼接
new_data = torch.cat([data1, data2], dim=2)
print(new_data)
print(new_data.shape)
'''
输出结果:
tensor([[[7, 8, 7],
[6, 3, 6]]])
tensor([[[3, 6, 5],
[7, 5, 0]]])
tensor([[[7, 8, 7],
[6, 3, 6]],
[[3, 6, 5],
[7, 5, 0]]])
torch.Size([2, 2, 3])
tensor([[[7, 8, 7],
[6, 3, 6],
[3, 6, 5],
[7, 5, 0]]])
torch.Size([1, 4, 3])
tensor([[[7, 8, 7, 3, 6, 5],
[6, 3, 6, 7, 5, 0]]])
torch.Size([1, 2, 6])
'''

自动微分模块

训练神经网络时，最常用的算法就是反向传播。在该算法中，参数（模型权重）会根据损失函数关于对应参数的梯度进行调整。为了计算这些梯度，PyTorch内置了名为 torch.autograd 的微分引擎。它支持任意计算图的自动梯度计算：

• 计算流程：
  • 前向计算得到预测值
    z=x∗w+bz = x*w + bz=x∗w+b
  • 计算损失函数（如MSE）
    loss=MSE(z,y)loss = \text{MSE}(z, y)loss=MSE(z,y)
  • 调用loss.backward()进行梯度回传
  • 通过grad属性获取梯度值
• 关键属性：requires_grad=True标记需要计算梯度的张量。
• 梯度意义：梯度大小反映参数更新速度，梯度越大表示减小损失的速度越快。

import torch
# 1. 当X为标量时梯度的计算
def test01():
x = torch.tensor(5)
# 目标值
 y = torch.tensor(0.)
# 设置要更新的权重和偏置的初始值
 w = torch.tensor(1., requires_grad=True, dtype=torch.float32)
b = torch.tensor(3., requires_grad=True, dtype=torch.float32)
# 设置网络的输出值
 z = x * w + b # 矩阵乘法
 # 设置损失函数，并进行损失的计算
 loss = torch.nn.MSELoss()
loss = loss(z, y)
# 自动微分
 loss.backward()
# 打印 w,b 变量的梯度
 # backward 函数计算的梯度值会存储在张量的 grad 变量中
 print("W的梯度:", w.grad)
print("b的梯度", b.grad)
'''
输出结果:
# 当X是标量时的结果
W的梯度: tensor(80.)
b的梯度 tensor(16.)
'''

 什么是归一化，什么是标准化？

　　归一化和标准化是数据预处理中常用的两种方法，旨在消除不同特征间的量纲差异，使数据更适合算法处理。‌归一化（Normalization）‌ 通常将数据线性缩放到固定区间（如），而‌标准化（Standardization）‌ 则通过调整数据分布使其均值为0、方差为1。‌

归一化的定义与特点

归一化通过最小-最大缩放将数据映射到特定范围，公式为：
x′=x−min⁡(x)max⁡(x)−min⁡(x)x′=max(x)−min(x)x−min(x)​
其中 xx 为原始数据，x′x′ 为归一化后的值。其核心特点是：‌

• ‌缩放范围固定‌：结果严格限定在预设区间（如），便于直观比较。‌
  
• ‌对极值敏感‌：最大值和最小值易受异常点影响，鲁棒性较差，适合数据分布稳定、无极端值的场景。‌

标准化的定义与特点

标准化（如Z-score标准化）通过计算均值和标准差调整数据分布，公式为：
x′=x−μσx′=σx−μ​
其中 μμ 为均值，σσ 为标准差。其核心特点是：‌

• ‌分布中心化‌：处理后数据均值为0，方差为1，符合标准正态分布。‌
  
• ‌抗干扰性强‌：异常值对均值的影响较小，适合噪声较多或数据分布未知的场景。‌

主要区别

1. ‌缩放依据‌：
   • 归一化依赖数据极值（最小/最大值）。‌
     
   • 标准化依赖整体统计量（均值和标准差）。‌
     
2. ‌输出范围‌：
   • 归一化结果固定。‌
     
   • 标准化结果无固定范围，可能超出[-1,1]。‌‌
     
‌鲁棒性‌（是系统、算法或事物在面临异常、不确定性或意外情况时,仍然能够保持其功能、性能以及稳定性的能力）：
• 归一化易受异常值干扰。‌
• 标准化对异常值更稳健。‌

 

 

 

 

 

参考：

原文链接：https://blog.csdn.net/weixin_41599072/article/details/143169138

https://blog.csdn.net/IT_ORACLE/article/details/146803548