题解

传送门 P7528 [USACO21OPEN] Portals G

题意

有 $2n$ 个点可以通过对应的传送门到另一个点，
并且可以将一组的传送门消 $c_i$，
将一组的四个传送门以任意序交换。
求将所有点连通的最小价值。

首先观察样例的形成图。

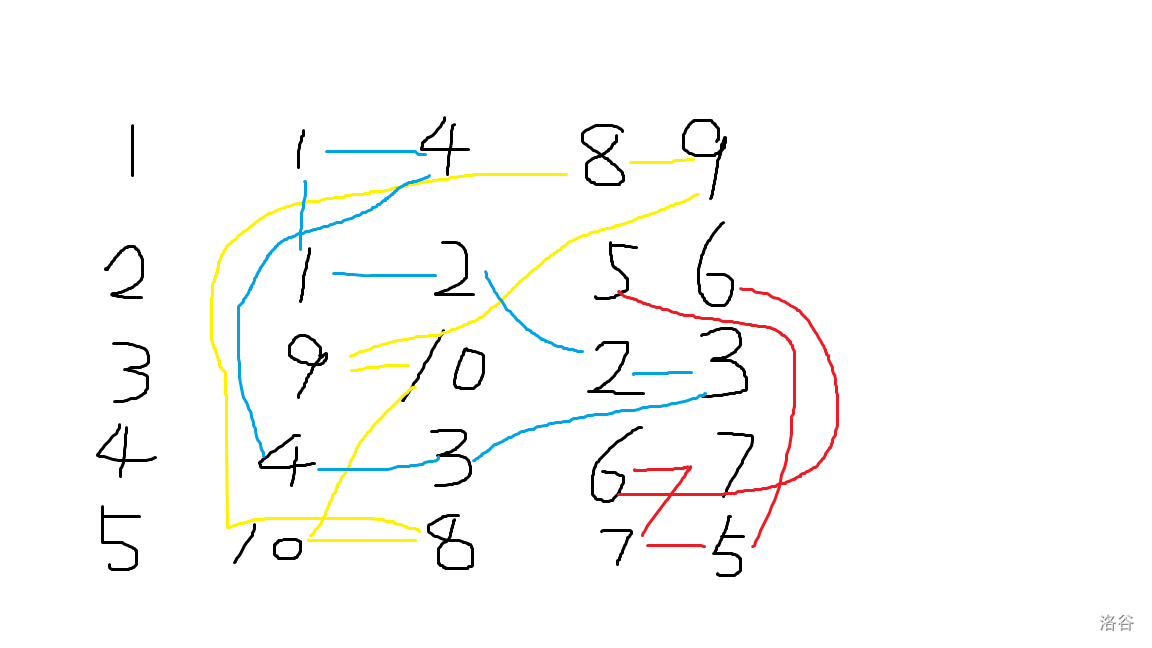
不同颜色代表不可互达。

整理一下
将第 1 列名为 $1\sim n$，
第 2 列为 $n+1\sim 2n$，
......

于是就有了这样的图。

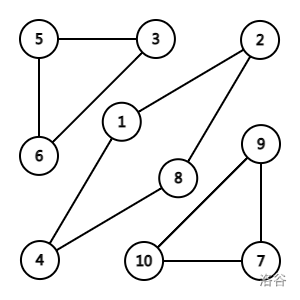
题意还给了一种方式----交换传送门。
即我们对于第 $i$ 个传送门， 可以将 $i$ 到 $i+n$ 的边与 $i+2n$ 到 $i+3n$ 的边切断， 连接 $i$ 与 $i+2n$ 和 $i+n$ 与 $i+3n$ 的边；
或
连接 $i$ 与 $i+3n$ 和 $i+n$ 与 $i+3n$ 的边。

假设对第一组进行交换。

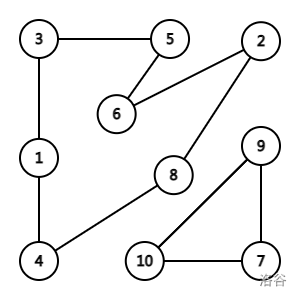
可以明显观察出有两组环进行了合并。

于是可以想到： 对于第 $i$ 组，如果两个点不在一组中，那么我们就可以用 $c_i$ 的代价讲第这两个点所属的环合并。

于是代码的总思路就形成了： 以 $c_i$ 与其对应 $id$ 从小到大排序，
对于排序后的第 $i$ 位，判断其两端是否在一个并查集，否则消耗 $c_i$ 合并。

AC 代码如下

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n, m;
int ans;
int fa[N*2];//并查集
int door[N*2];//门
struct node {
    int val;
    int id;
} d[N];
bool cmp(node a,node b){
    return a.val<b.val;
}
int root(int x) {//并查集find
    return fa[x]=fa[x]==x?x:root(fa[x]);
}
void hb(int a,int b) {//合并两个并查集
    fa[root(a)]=root(b);
}
bool checK(int a,int b) {//看是否在同一并查集
    return root(a)==root(b);
}
signed main() {
    cin>>n;
    for(int i=1; i<=2*n; ++i) {//初始化
        fa[i]=i;
    }
    for(int i=1; i<=n; ++i) {
        int a,b,c,e;
        cin>>d[i].val;d[i].id=i;
        scanf("%d%d%d%d",&a,&b,&c,&e);
        if(door[a]) hb(door[a],i);
        if(door[b]) hb(door[b],i);
        if(door[c]) hb(door[c],i+n);
        if(door[e]) hb(door[e],i+n);
      //合并对应的门
        door[a]=i;
        door[b]=i;
        door[c]=i+n;
        door[e]=i+n;
    }
    sort(d+1,d+n+1,cmp);
    for(int i=1;i<=n;++i){
        if(!checK(d[i].id,d[i].id+n)){
            ans+=d[i].val;
            hb(d[i].id,d[i].id+n);
        }
    }
    cout<<ans;
    return 0;
}