题解P6677 [COCI2019-2020#2] Checker

传送门 P6677 [COCI2019-2020#2] Checker

题意

将一个 $n$ 多边形用 $n-3$ 条边分裂成 $n-2$ 个三角形。每条边有三种颜色。

• 如果分裂方式是错误的，输出 neispravna triangulacija。
• 如果对于分裂出的三角形，每个三角形三条边都不相同，输出 tocno。
• 否则，输出 neispravno bojenje。

分析

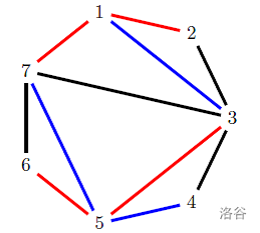
在只知道周围与一条内边的情况下，
对于 $(3,5,7)$ 这个三角形，我们并不能快速知道这个三角形的三边是否合法。
但是对于 $(3,4,5)$ 这个三角形，我们却可以马上判断，因为这个三角形的形状是由两个边缘与一条内边组成。

于是我们可以从间隔为 1 的内边开始，从间隔逐一增大缩边，如果有一条内边的左右不能组成由两个边缘与一条内边的三角形，那么这个分割方案就是不成立的。(应该显然吧。)

实现

然后逐一实现。

1. 间隔 $\min ((v+n-u)\bmod n,(u+n-v)\bmod n)$。

2. 缩点：

   //l[i],r[i]是i左右的边，col[i]是i左侧边的颜色，cor[i]则是右边
   l[v]=u,r[u]=v;
   col[v]=cor[u]=co;

   注意

3. $T$ 是这个数据对应的 Subtask 编号，而不是多组输入。（考试时以为是多组输入暴错。）

4. 要用 mark 记录已经缩的节点，缩边前检查节点。

激动人心的代码环节

Code