题解 P9350 [JOI 2023 Final] Advertisement 2

传送门

题意

在一个数轴上有 $n$ 个人，第 $i$ 个人位于坐标 $X_i$，权值为 $E_i$。我们要送给一些人书，当 $i$ 收到了一本书，那么对于所有 $j$，满足 $\left | X_i-X_j \right | \le E_i-E_j$，那么 $j$ 会去买一本书。问最少送几个人书会使得所有人都有一本书。

切分

部分分 1（特殊性质）

所有的 $E_i$ 都相等，说明除了在同一个点的人，其他任何人无法进行传递，记录一共有多少个不同坐标即为答案。

部分分 2（$n\le16$）

对于这个部分分，明显是让我们以二进制枚举来解决，枚举每一种状态，判断是否可行，最后在可行的方案间取 min。

部分分 3（$n\le 10^3$）

观察我们的判断的式子，我们可以分析出两个性质：

1. 我们只有可能由一个 $E_i$ 更大的转移到更小的，
2. 倘若 $i$ 能影响到 $j$，$j$ 能影响到 $k$，$k$ 必然也能直接被 $i$ 影响。这也代表，倘若我们当前点已经被影响，我们不需要再选择当前点。

由此，我们可以从 $E$ 值由大到小排序，假如当前点没有被影响过，那么枚举每个点，观察是否能被影响。否则跳过。

int tot=0;
for(int i=1;i<=n;++i) {
    if(vis[i]) continue;
    ++tot;
    for(int j=i+1;j<=n;++j)
        if((a[i].E-a[j].E)>=(abs(a[i].x-a[j].x))) 
            vis[j]=1;
}
cout<<tot;  

时间复杂度：$O(n^2)$。

正解

对于这种绝对值的式子题，我们应当在第一时间想到把绝对值拆掉，有很多的题目都可以通过这样的方式转化成二维偏序，三维偏序问题。对于此题，我们也用拆绝对值的方式。

我们可以得到：$X_i-X_j \le E_i-E_j \operatorname{and} X_j-X_i \le E_i-E_j $。
再将下标相同的放在同一边：$E_j-X_j \operatorname{and} E_j+X_j \le E_i+X_i$。
令 $x_i=E_i+X_i$，$y_i=E_i-X_i$，
以此在二维坐标上标记这些点（是否离散化皆可，但是图上以离散化更加明显）。
以样例一为例（省去了离散化的过程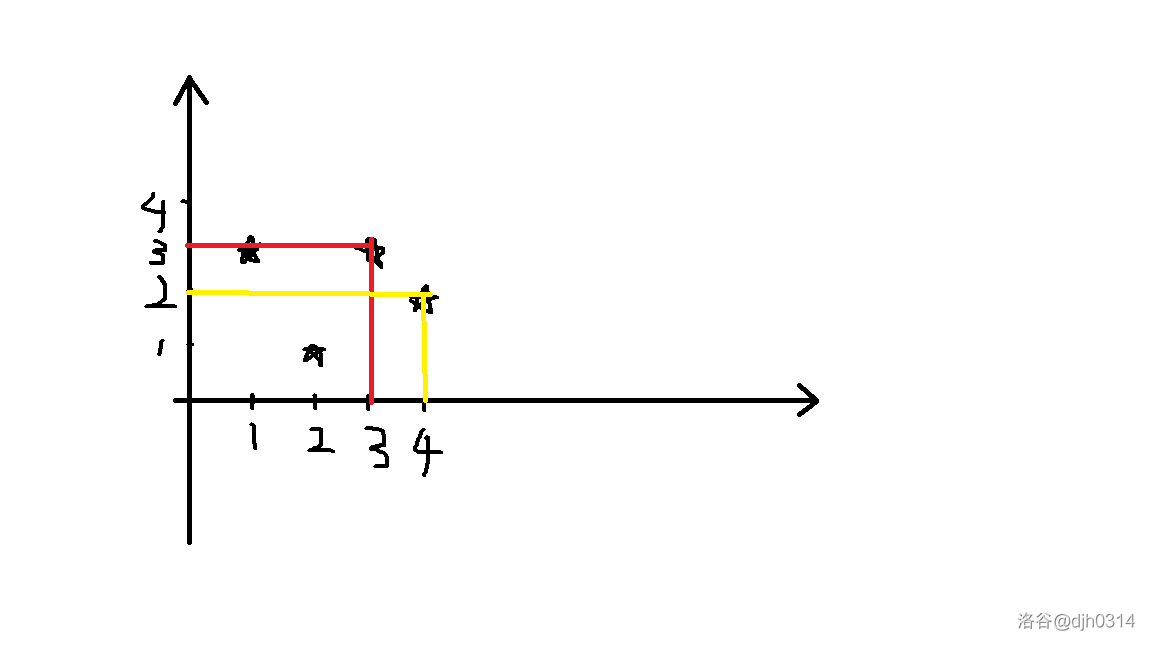）， 也许这还不够明显，再看看样例三的构图，

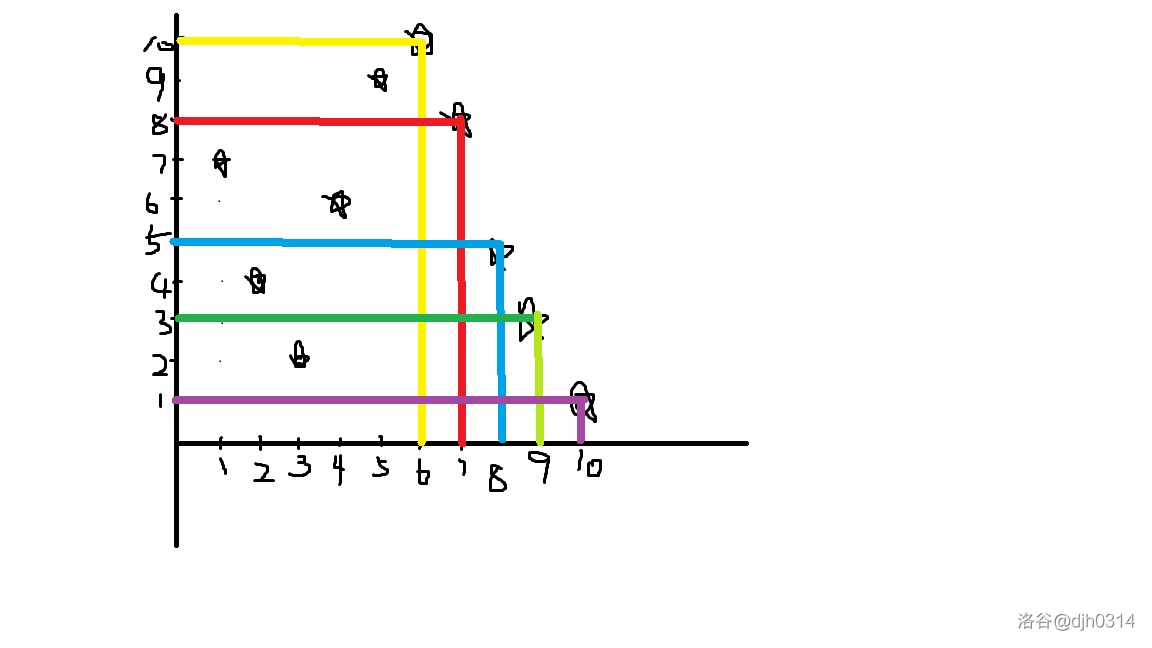
应该明显吧，我们最后的取的点必然不能被其他点所覆盖，这也就导致，我们最后取得点将会构成一个单调下降的序列。

由此，我们用一个单调栈维护，最后答案就是留下来的数的数量。

sort(a+1,a+n+1);
for(int i=1;i<=n;++i) {
    while(top&&a[q[top]].y<=a[i].y) --top;
    q[++top]=i;
} 
cout<<top;

时间复杂度：$O(n\log {}{n})$。

总结一下，我们的正解先将原来的输入转化，然后以 $x$ 排序再求一个单调栈即可，建议评绿，tag 为单调栈。