题解 疯狂的动态树

来自 OJ 的一道题（疑似 CF）。

题意

一棵边权都为 $1$ 的数，初始根为 $1$ 号节点，有 $m$ 次操作：

1. 0 u 将根换成 $u$。
2. 1 u v 询问 $u$ 到 $v$ 路径上所有节点的深度和。
3. 2 u 询问以 $u$ 为根的子树的所有节点深度和。

根节点深度为 $0$。

分析

首先从部分分打起，暴力换根，每次换根操作重新跑一边 dfs，对于路径查询可以用等差数列或倍增解决。
时间复杂度：$O(n^2)$，但是可以拿下没有换根操作的数据点。

正解

这里提供一个现场想出来的，思维最简单的方法。尽管是最长的。

首先分析一下换根所带来的影响，自然是深度会发生变化，那么我们考虑一下真正维护一下每个节点的深度。

考虑一下如何实时维护我们的深度，发现我们在跨越若干个节点时很难进行快速维护，这时，我们尝试一步一步移动。

观察一下图，此时我们需要将根从 $1$ 转移到 $7$。

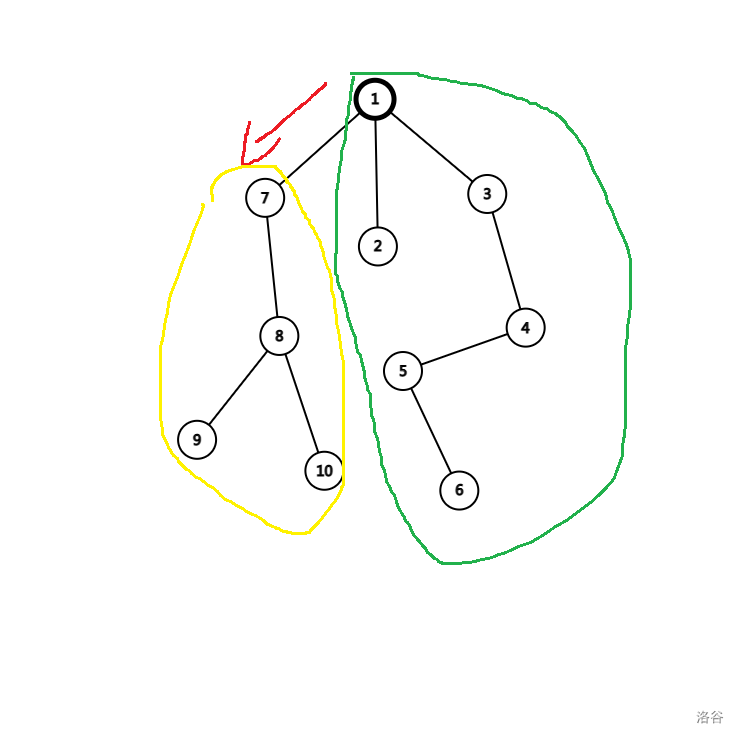
可以发现，我们绿色框的所有节点的深度都 +1，我们黄色框出来的节点深度都 -1。

如此，我们发现，我们只要维护了区间子树的加减就可以维护一步一步的的换根。

如此，我们先确定了两个步骤：换根 DP，线段树。

接下来分析我们的查询操作。

子树查询

在维护线段树的同时，自然可以维护区间和，我们可以分类讨论来解决在确定根时的子树和（令查询的节点为 $u$，根为 $rt$）。

$rt$ 在 $u$ 的子树中

这时一个经常遇到的题型，找到 $u$ 在 $rt$ 方向上的亲儿子，然后所有减去这个节点即可。

$rt$ 和 $u$ 是同一个节点

即所有节点的深度和。

另外情况

区间查询即可。

路径查询

路径查询搭配上线段树，很难不想到我们的树链剖分啊，因此使用树链剖分。

总结一下

我们这道题需要先离线，换根，树链剖分，线段树即可。

很简单是吧，那就用 150 行代码来愉快地 A 掉他吧。

都是板子，所以不贴代码了。