红黑树
红黑树
杂话
最近闲来无事去学了学红黑树,《算法导论》和维基百科都讲的很详细。
红黑树(英语:Red–black tree)是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型用途是实现关联数组。它在1972年由鲁道夫·贝尔发明,被称为“对称二叉B树”,它现代的名字源于Leo J. Guibas和罗伯特·塞奇威克于1978年写的一篇论文。红黑树的结构复杂,但它的操作有着良好的最坏情况运行时间,并且在实践中高效:它可以在\(O(\log n)\)时间内完成查找、插入和删除,这里的 \(n\) 是树中元素的数目。 ————维基百科
关于红黑树名字的来源也有一个不错的故事(奇怪的名字总会引人遐想:在一篇1972年的论文〈A Dichromatic Framework for Balanced Trees〉中,Leonidas J. Guibas 和 Robert Sedgewick从对称二元B树(symmetric binary B-tree)中推导出了红黑树。之所以选择“红色”是因为这是作者在帕罗奥多研究中心公司(Xerox PARC)工作时用彩色激光打印机可以产生的最好看的颜色。另一种说法来自Guibas,是因为红色和黑色的笔是他们当时可用来绘制树的颜色。故事依旧来自维基百科。
我主要只看了《算法导论》,维基百科只是掠过一眼,所以如果算导和维基上有不一样的我只能按算导来写,不过算导上那个删除操作我看的时候就很惊奇于算导的谜之解释,所以这里按维基上的来,这也是我看算导时想的,不过解释不一样代码都是一样的。
通过本身的性质来维护平衡性,真的tql
性质
红黑树的基本属性有五个:\(key\)值,左儿子地址,右儿子地址,父亲地址和它的颜色(红或黑)。
红黑树需要满足以下几点性质:
- 每个点是红色的,或者是黑色的
- 根结点是黑色的
- 每个叶结点(\(NIL\))是黑色的
- 如果一个结点是红色的,那么它的两个子结点都是黑色的
- 对于每个结点,其到其所有后代叶结点的简单路径上黑色结点的个数是相等的

为了便于处理边界条件,使用一个哨兵结点来代替所有 \(NIL\)
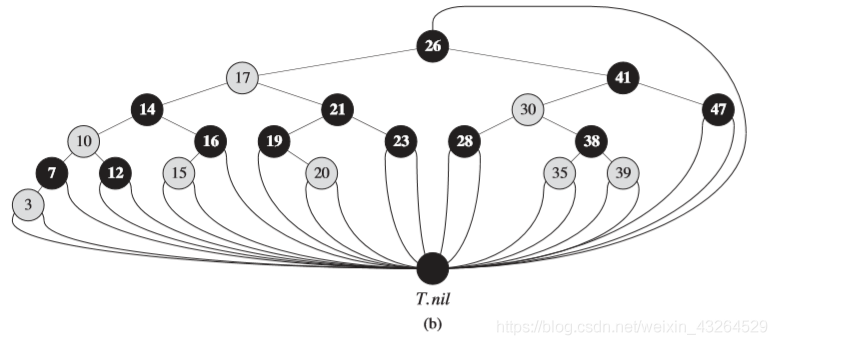
那么,为什么只要维持这几点性质就可以维持树的平衡呢?因为满足红黑性质的树一定是一棵比较平衡的树,对于一个具有 \(n\) 个内部结点的树,它的高度至多有 \(2\lg(n+1)\)。算导上有严谨的解释,我在这里简单说一下我的理解:首先我们先不看红色结点,那么黑高是一定的,如果去掉所有红色结点,那么这棵树就是高度平衡的,就算往里添加红色结点,死劲按着一条路径加,根据性质四,这条路径的高度至多变成原来的两倍。因此,平衡树的各种操作在红黑树的执行时间都是 \(O(\lg n)\)。
旋转
和其他平衡树的旋转一样,分为左旋右旋。
 (抠图永无止境……)
(抠图永无止境……)
直接贴代码了:
void left_rotate(int x) {
int y = t[x].r;
t[x].r = t[y].l;
if (t[y].l != -1)
t[t[y].l].p = x;
t[y].p = t[x].p;
if (t[x].p == nil) root = y; //特殊设定的nil结点,让nil = maxn - 1;
else if (t[t[x].p].l == x)
t[t[x].p].l = y;
else t[t[x].p].r = y;
t[x].p = y;
t[y].l = x;
}
void right_rotate(int x) {
int y = t[x].l;
t[x].l = t[y].r;
if (t[y].r != -1)
t[t[y].r].p = x;
t[y].p = t[x].p;
if (t[x].p == -1) root = y;
else if (t[t[x].p].l == x)
t[t[x].p].l = y;
else t[t[x].p].r = y;
t[x].p = y;
t[y].r = x;
}
插入
插入操作与二叉搜索树的插入操作差不多,将插入结点插入到叶结点,然后左右结点设为 \(nil\) ,并且将颜色设为红色。操作会破坏红黑性质,所以后来又进行红黑性质的维护。
为什么要设为红色呢?直接设为黑色不久不用违反性质4了吗?但是如果直接设为黑色会影响性质5,在不改变其他结点颜色的情况下性质5是不可能被修复的,窃以为这样较为复杂所以不采用。而且决定红黑树的时间复杂度的关键是黑高,若设定为黑色可能会有多增黑高的可能,这些是个人理解,可能不对。
void insert(int z) {
int y = nil, x = root;
while (x != -1) {
y = x;
if (t[z].k < t[x].k) x = t[x].l;
else x = t[x].r;
}
t[z].p = y;
if (y == -1) root = z;
else if (t[z].k < t[y].k)
t[y].l = z;
else t[y].r = z;
t[z].l = -1;
t[z].r = -1;
t[z].c = 0;
insert_fixup(z);
}
注意到结尾的 \(insert\_fixup\) 函数,这个就是用来修复红黑性质的函数。
void insert_fixup(int z) {
while (t[t[z].p].c == 0) {
if (t[z].p == t[t[t[z].p].p].l) {
int y = t[t[t[z].p].p].r;
if (t[y].c == 0) { //case 1
t[t[z].p].c = 1;
t[y].c = 1;
t[t[t[z].p].p].c = 0;
z = t[t[z].p].p;
}
else if (z == t[t[z].p].r) { //case 2
z = t[z].p;
left_rotate(z);
}
t[t[z].p].c = 1; //case 3
t[t[t[z].p].p].c = 0;
right_rotate(t[t[z].p].p);
}
else {
int y = t[t[t[z].p].p].l;
if (t[y].c == 0) {
t[t[z].p].c = 1;
t[y].c = 1;
t[t[t[z].p].p].c = 0;
z = t[t[z].p].p;
}
else if (z == t[t[z].p].l) {
z = t[z].p;
right_rotate(z);
}
t[t[z].p].c = 1;
t[t[t[z].p].p].c = 0;
left_rotate(t[t[z].p].p);
}
}
t[root].c = 1;
}
共分为6种情况,其中 \(z\) 的父结点是左儿子还是右儿子是对称的,把 \(right\) 和 \(left\) 对换就行,以左儿子为例,分为三种情况:
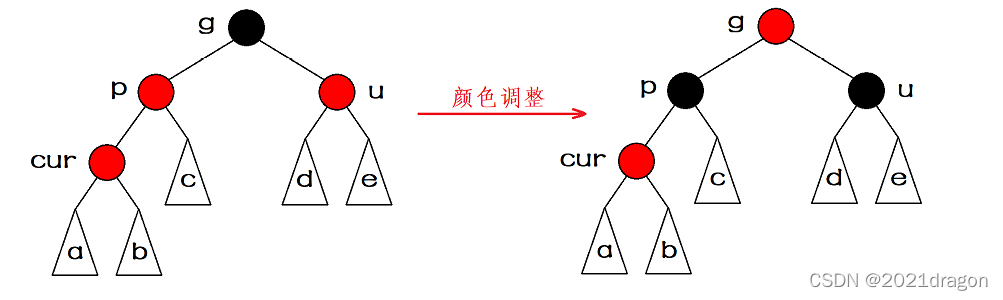
情况一:插入结点的叔叔存在,且叔叔的颜色是红色。
为了避免出现连续的红色结点,我们可以将父结点和叔结点变黑,将祖父结点变红。这样一来既保持了每条路径黑色结点的数目不变,也解决了连续红色结点的问题。
但是这样就出现一个新的问题:祖父结点就可能不满足红黑性质了,于是我们将祖父结点设为新的 \(z\) 继续修改。
还有一个问题是:如果 \(g\) 正好是根结点了怎么办?所以在每次循环的末尾都要将根结点设为黑色,只有这个时候红黑树的黑高才会增加。
情况二:插入结点的叔结点存在,且叔结点的颜色是黑色,并且 \(z\) 是一个右孩子。
我们直接左旋一下,使它变成情况三
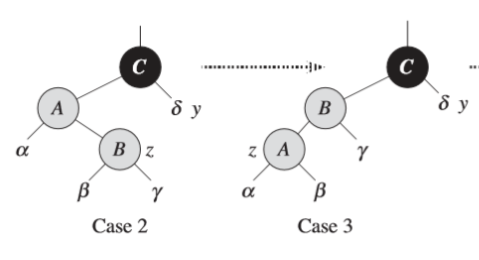
情况三:插入结点的叔结点存在,且叔结点的颜色是黑色,并且 \(z\) 是一个左孩子。
出现叔叔存在且为黑时,单纯使用变色已经无法处理了,这时我们需要进行旋转处理。祖孙三代的关系是直线(x、父亲、祖父这三个结点为一条直线),正是情况三,则我们需要先进行单旋操作,再进行颜色调整,颜色调整后这棵被旋转子树的根结点是黑色的,因此无需继续往上进行处理。
因为只有一条直线才能旋起来,所以情况二就先处理成情况三。
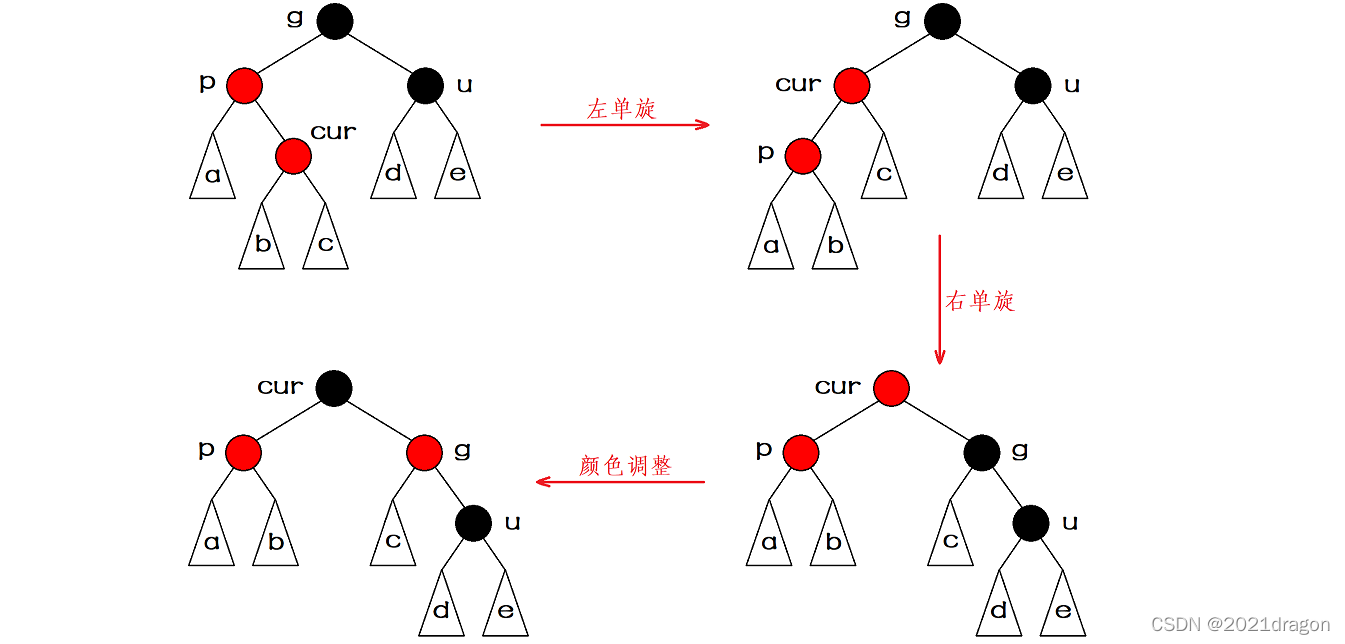
有的博客将叔结点不存在还算成了一种情况,其实是多余的,因为叔结点不存在既是 \(nil\) ,而 \(nil\) 的颜色是黑的,等同于情况二和情况三。
对于 \(fixup\) 操作维持红黑树性质的严谨证明,算法导论上说的很详细,但奈何我非常懒不想再抄一遍并且找不到电子书来截图……
时间复杂度是 \(log\)
并且我们注意到插入实际上是原地算法,因为上述所有调用都使用了尾部递归。
删除
RB-delete删除 = 二叉树的删除+删除修复(delete_fixup)
做二叉树删除时,需要记录被调整节点的颜色。
二叉搜索树删除的四种情况
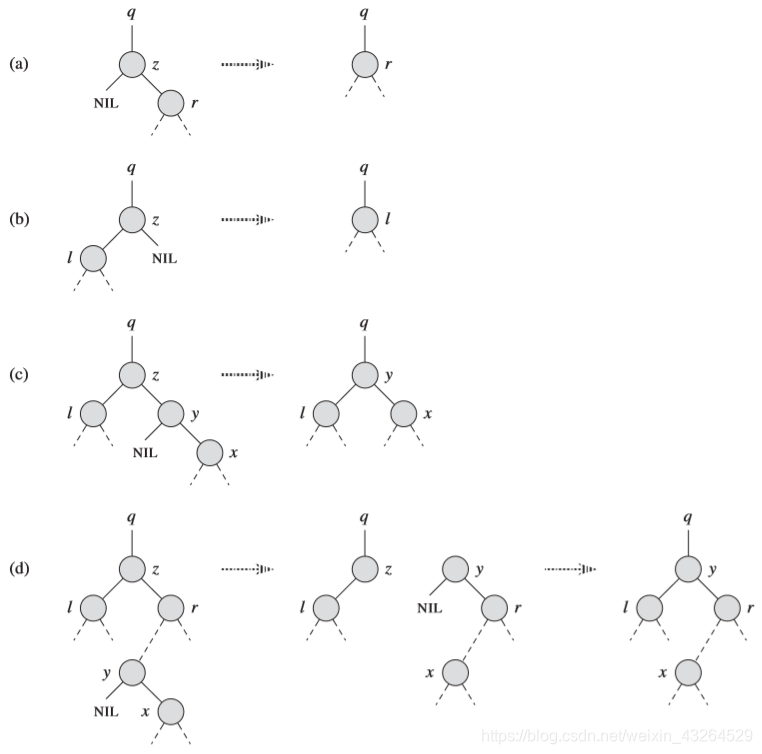
void rb_delete(int z) {
int y = z;
bool delcol = t[y].c;
int x = z;
if (t[z].l == nil) {
x = t[z].r;
rb_transplant(z, t[z].r);
} else if (t[z].r == nil) {
x = t[z].l;
rb_transplant(z, t[z].l);
} else {
y = find_min(t[z].r);
delcol = t[y].c;
x = t[y].r;
if (t[y].p == z)
t[x].p = y;
else {
rb_transplant(y, t[y].r);
t[y].r = t[z].r;
t[t[y].r].p = y;
}
rb_transplant(z, y);
t[y].l = t[z].l;
t[t[y].l].p = y;
t[y].c = t[z].c;
}
if (delcol == 1)
rb_delete_fixup(x);
}
为什么要记录被调换的那个 \(y\) 结点的颜色呢?而且我们注意到只有被调整结点颜色为黑色时才会进行调整操作,这是因为删除节点之前性质5是满足的,但是如果在一条路径上去掉一个结点,并且这个结点是黑色的,那么性质5显然就不满足了,所以要进行调整。算法导论上将修改操作解释为“认为改变后的结点有双重颜色,破坏了性质1,故进行修复操作来恢复性质1、性质2、性质4”,窃以为多此一举,不如按维基百科上破坏性质5解释来的自然。
先给出 \(fixup\) 代码:
void rb_delete_fixup(int x) {
while (x != root && t[x].c == 1) {
if (x == t[t[x].p].l) {
int w = t[t[x].p].r;
if (t[w].c == 0) { //A: CASE 1
t[w].c = 1;
t[t[x].p].c = 0;
left_rotate(t[x].p);
w = t[t[x].p].r;
}
if (t[t[w].l].c == 1 && t[t[w].r].c == 1) { //A: CASE 2
t[w].c = 0;
x = t[x].p;
} else {
if (t[t[w].r].c == 1) { //A: CASE 3
t[t[w].l].c = 1;
t[w].c = 0;
right_rotate(w);
w = t[t[x].p].r;
}
t[w].c = t[t[x].p].c; //A: CASE 4
t[t[x].p].c = 1;
t[t[w].r].c = 1;
left_rotate(t[x].p);
x = root;
}
} else {
int w = t[t[x].p].l;
if (t[w].c == 0) { //B: CASE 1
t[w].c = 1;
t[t[x].p].c = 0;
right_rotate(t[x].p);
w = t[t[x].p].l;
}
if (t[t[w].r].c == 1 && t[t[w].l].c == 0) { //B: CASE 2
t[w].c = 0;
x = t[x].p;
} else {
if (t[t[w].l].c == 1) { //B: CASE 3
t[t[w].r].c = 1;
t[w].c = 0;
left_rotate(w);
w = t[t[x].p].l;
}
t[w].c = t[t[x].p].c; //B: CASE 4
t[t[x].p].c = 1;
t[t[w].l].c = 1;
right_rotate(t[x].p);
x = root;
}
}
}
t[x].c = 1;
}
分为4种情况:
情况一:\(X\) 的兄弟结点 \(w\) 是红色的
当待删除结点的兄弟为红色时,我们先以父亲为旋转点进行一次左单旋,再将兄弟的颜色变为黑色,将父亲的颜色变为红色,此时我们再对结点 \(x\) 进行情况分析,情况一就转换成了情况二、三或四。
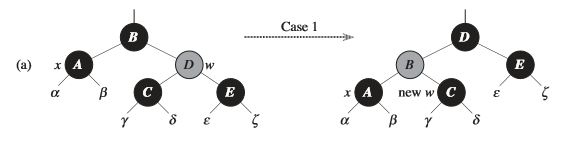
当结点 \(w\) 为黑色时,属于情况2、3、4,这些情况是由 \(w\) 的颜色来区分的。
情况二:\(x\) 的兄弟结点是黑色的,且 \(w\) 的两个子结点是黑色的
因为在删除时将 \(B-X\) 这一路的结点提上去一个,所以这一路的黑色结点显然少一个。
在该情况下,我们直接将兄弟的颜色变成红色,此时根据父亲的颜色决定红黑树的调整是否结束,若父亲的颜色是红色,则我们将父亲变为黑色后即可结束红黑树的调整;若父亲的颜色原本就是黑色,则我们需要将父亲结点当作下一次调整时的 \(x\) 结点进行情况分析,并且情况二在下一次调整时可能会是情况一、二、三、四当中的任何一种。

情况三: \(x\) 的兄弟结点是黑色的,且 \(w\) 的左儿子是红色,右儿子是黑色
出现该情况时,我们先以兄弟为旋转点进行一次右单旋,再将兄弟结点变为红色,将兄弟结点的左儿子变为黑色,此时我们再对 \(x\) 进行情况分析,情况三就转换成了情况四。
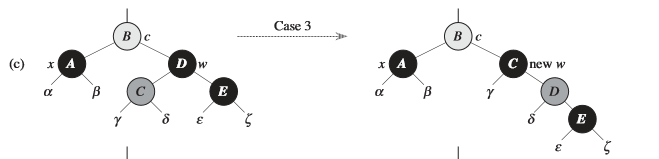
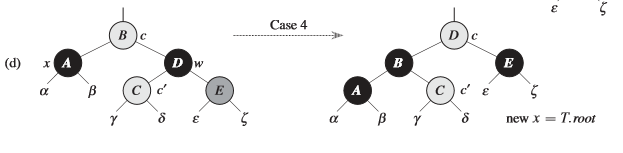
情况四:\(x\) 的兄弟结点是黑色的,且 \(w\) 的左儿子是黑色的,右儿子是红色的
经过情况四的处理后,红黑树就一定调整结束了。在情况四当中,我们先以父亲为旋转点进行一次左单旋,然后将父亲的颜色赋值给兄弟,再将父亲的颜色变为黑色,最后将 \(w\) 的右儿子变为黑色,此时红黑树的调整便结束了。
后记
真的是写前踌躇满志,写时痛苦面具,写后怅然若失。自己对于红黑树依旧是没有怎么掌握,只能不断地翻书查资料,书上写的有些过于严谨导致读来不畅,网上的博客大部分也只是介绍了一下操作,然而原理还是有些地方不懂,而有一些博客看上去似乎非常好但是太长了我也不敢看。
现在仍然有一些缺陷:
-
首先是代码,网上的都是用指针实现的,但是我对于指针实在是不太熟练,而且听说有一些地方用指针反而会慢一些,所以用的是数组,但是我太烂了,写了几个基本操作就放弃了,想要测试一下代码对不对总不能手推树的结构然后输出检验吧,那样太繁琐了,我竟没有知道这代码对不对了
-
然后则是一些原理仍不是很明白,反应在这篇博客中也是语焉不详,譬如,fixup操作,为什么要那样做?尤其是delete_fixup的解释,是解释成破坏性质1还是性质5?算导的固然不自然,在解释时似乎能自圆其说,但推敲一番觉得情况二“同时去掉一重黑色”的解释很怪异,似乎在说底色是红色,然后x染了两重黑,w是一层,但是去掉后w岂不就无色了?底色可以看作红黑色,那我两重黑色就不是红黑色了?然而如果用性质5我却无法证明。
-
还有一点是对于那些操作的描述,由于都是相同的,我自己懒得写,于是只能搬一下了,还有图也是,这导致这篇文章像一个缝合怪,有的地方颇不自然
upd:把代码给gpt看了一下,似乎没什么问题,当然,gpt很多时候不靠谱;查询没写,不过是一样的

 红黑树的基本操作
红黑树的基本操作

 浙公网安备 33010602011771号
浙公网安备 33010602011771号