拾荒记
机房圣经
——摘抄自某位OIer
-
我只需要接爱自己是个废物的事实就好了。
-
这种题正式考试不可能考,我不会也没关系。
-
这种题不是我擅长的类型,我不会也挺正常。
-
这题不就是乱搞,我考场上想的也差不多,没啥意思。
-
这题看懂题解就差不多了,懒得补了。
-
—次考试也说明不了什么,考不好不用慌。
-
这场是真的太难了,我考不好不是我的问题。
-
这种地方挂掉只是运气问题,跟我没啥关系。
-
这我只是模拟赛在乱打,正式赛会好好打的。
-
虽然我最近考试比较拉,但是我两万年前阿克了一场模拟赛,所以我还是有水平的。
-
打不过某某也没办法,人家本来就比我强。
-
某某虽然以前比我弱,但是现在比我强了,但是这也是没办法的事嘛。
-
某某这种神仙,同期比我强也挺正常的。
-
我比某某神仙同期强,看来我还是很厉害的。
-
没必要跟别人比,我觉得我做得够好了。
-
就摸一下也没啥关系吧,反正会工作的。
-
今天的任务反正已经完成了,吃饭前的时间就摸过去吧。
-
我每天就摸中午这么一小会,也不算很摸。
-
写得太累了,去摸一会,就当合理放松。
-
常言道没有一次通宵解决不了的ddl',我当天再搞吧。
-
我还有别的题要做,我把这题咕了合情合理。
-
虽然我比较菜,但是做到balabala多半还是没问题的,所以不需要担心。
-
我才高一,我还剩一年,就算明年NOI也还剩九个月,时间挺多的。
-
我干嘛要有能代表这个省的水平,没了我不还有一堆人嘛。
-
想摆烂但是找不到理由的时候欢迎来这里看看。如果对你有帮助的话我很高兴,祝你早日变得和我一样菜。
基本算法
贪心
简介
贪心算法(英语:greedy algorithm),是用计算机来模拟一个“贪心”的人做出决策的过程。这个人十分贪婪,每一步行动总是按某种指标选取最优的操作。而且他目光短浅,总是只看眼前,并不考虑以后可能造成的影响。
可想而知,并不是所有的时候贪心法都能获得最优解,所以一般使用贪心法的时候,都要确保自己能证明其正确性。 ——oi.wiki
贪心算法一般用于最优子结构问题,即为可以将一个问题拆分为多个子问题,由每个子问题的最优解可以推出整个问题的最优解。
特点
1.贪心选择
所谓贪心选择是说应用同一规则,将原问题变为一个相似的但规模更小的子问题,后面的每一步都是看目前的最佳选择,只依赖于已做出的选择,不依赖未作出的选择。
如背包问题,对于部分背包问题,是可以用贪心优先选择性价比高的,但对于这种不可分割物品的背包问题,却显然不能用贪心来做了,就比如说:
体积:100, 物品1:10 1, 物品2:100 100
如果按照贪心策略应该选物品一,这样就选不了物品二了,最大利益是 10, 而应该是只装物品二,最大利益 100 。此时显然贪心策略是错的了,因为它还要依赖其他物品,这时应该用动态规划解题。
2.最优子结构
执行算法时,每一次得到的结果虽然都是目前的最优解,但只有满足全局最优解包含局部最优解时,才能保证贪心算法正确。
证明方法
因为贪心往往不是正解,所以在使用贪心时往往要证明其正确性,而且有时证明其正确性时可以推出如何贪心(如国王游戏)。
证明贪心方法有两种:反证法和归纳法。很多基于贪心的算法也是通过这两种方法证明。
1.反证法
对于目前采取的贪心策略,定下一种交换方案,如果按照这种交换方案交换两个元素后,方案没有变得更优,那么说明目前的贪心策略是对的。
如求最小生成树的 \(Kruskal\) 算法其正确性就是反证法证明的。
2.归纳法
先算得出边界情况(例如 \(n == 1\) )的最优解 \(F_1\),然后再证明:对于每个 \(n\),\(F_{n + 1}\) 都可以由 \(F_n\) 推导出结果。
一些经典例题
1.最优装载问题
给定 \(n\) 个物品,第 \(i\) 个物品的重量是 \(w_i\) ,选择尽量多的物品,使总重量不多于 \(C\) 。
【贪心策略】 : 优先选择最轻的。
2.部分背包问题
与上一个例子不同,本题还加入了一个价值 \(v_i\) ,所以用 \(\frac{v_i}{w_i}\) 来表示一件物品的性价比。
【贪心策略】 : 优先选择性价比高的。
3.乘船问题
有 \(n\) 个人,第 \(i\) 个人重量为 \(w_i\) 。每艘船最大载重量为 \(C\) ,最多盛两个人。求如何用最少的船装载所有人。
【贪心策略】 : 对于任意一个人,应该选择能和他一起坐船的人中最重的一个。
4.选择不相交区间
给定 \(n\) 个开区间 \((a_i, b_i)\),选择尽量多的区间,使得他们两两没有公共点。
【贪心策略】 :
5.区间覆盖问题
给定 \(n\) 个闭区间 \([a_i, b_i]\) ,选择尽量少的区间,使其完全覆盖给定区间。
二分
搜索
递推与递归
宏观描述
对于待求解的一个问题,如果
数据结构
基础数据结构
栈 stack
STL: stack
链表 vector
队列 queue
并查集
基本并查集
//查询
int find(int k){
if(f[k] == k) return k;
return f[k] = find(f[k]);
}
//合并
int merge(int x, y){
f[find(x)] = find(y);
}
并查集进阶应用
边带权 (模板:P1196 [NOI2002] 银河英雄传说 )
在本道题中要查询两个战舰之间所隔战舰,整个结构是许多条链,而每条链其实也是一颗特殊的树,可以用边带权的并查集来做。
拓展域 拆点
ST表
ST表是基于倍增思想实现的,用于求静态区间最大值。
#include <bits/stdc++.h>
#define maxn 500005
#define int long long
using namespace std;
const int mod = 998244353;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int n, m, f[maxn][20];
signed main() {
n = read(), m = read();
for (int i = 1; i <= n; i++) f[i][0] = read();
for (int j = 1; j <= log(n) / log(2) + 1; j++)
for (int i = 1; i <= n; i++)
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
for (int i = 1; i <= m; i++) {
int l = read(), r = read();
int k = log(l - r + 1) / log(2);
cout << max(f[l][k], f[r - (1 << k) + 1][k]) << endl;
}
}
单调队列
如果一个选手比你小还比你强,那你就可以退役了
单调队列就是要保持元素下标和元素大小的双单调,当插入一个元素要破坏第二个单调性时,就要删除队列尾部的元素。
单调队列常用来优化DP
#include<bits/stdc++.h>
#define maxn 1000005
using namespace std;
int n, k;
int a[maxn], q[maxn];
void min_(){
int head = 1, tail = 0;
for(int i = 1; i <=n; i++){
while(head <= tail && a[q[tail]] >= a[i]){
tail --;
}
q[++tail] = i;
while(q[head] <= i-k) head ++;
if(i >= k) cout<< a[q[head]]<<" ";
}
}
void max_(){
int head = 1, tail = 0;
for(int i = 1; i <=n; i++){
while(head <= tail && a[q[tail]] <= a[i]){
tail --;
}
q[++tail] = i;
while(q[head] <= i-k) head ++;
if(i >= k) cout<< a[q[head]] <<" ";
}
}
int main(){
cin >> n >> k;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
min_();
cout <<endl;
max_();
}
单调栈
线段树
线段树是一个很优秀的树结构,较简单,功能多,可以维护复杂信息。 可以动态开点,可以打懒标记。
基本概念
线段树是基于分治思想的二叉树。
为了引入线段树,我们来看一个例子:
例 给你一个序列\(a\), 需要支持一下几种操作
1.查询区间\([l, r]\)上的值的和;
2.修改某一个位置上的值;
3.区间\([l, r]\)值\(+k\) ;
其实这是可以用前缀和来做的,但未免慢了些;前两个操作树状数组可以很简洁地完成,但第三个就有些麻烦了,而且效率也是不及线段树的。
类似于树状数组,线段树也是一个节点管理多个原数组的数的一些信息。
线段树的特点:
- 每个节点代表一个区间;
- 线段树具有唯一的根节点,代表区间是整个统计范围(可持久化除外,有多个);
- 线段树的每个叶子节点都代表一个长度为1的原区间\([x, x]\);
- 对于每个节点\([l, r]\) , 其左儿子是\([l, mid]\), 右儿子是\([mid + 1, r]\), 其中 \(mid = (l + r)/2\);
如图:
普通线段树的实现
线段树的存储
线段树是一种二叉树,所以我们可以采用父子二倍的方法来实现器存储。对于一个节点 \(p\) ,其左儿子是 \(p*2\) ,右儿子是 \(p*2+1\) 。
对于每个节点,都会存储一些信息,所以我们可以用一个结构体来存:
struct node{
int l, r;//这个节点所维护的区间
int dat;//这个节点所维护的区间的信息
}tree[4*maxn];
当然,也可以不用结构体,只要在调用相关函数时上传\([l, r]\) 信息即可。
我们可以看到,线段树数组开的空间是\(4*maxn\) ,这是为什么呢。首先我们可以从上图看到,对于整个区间长度是二的n次幂的区间,需要原数组二倍的空间(\(2n-1\)) ,而如果不是二的n次幂呢?那就会多一层,而多的那一层的所占空间是\(2n\) ,而且我们采用的父子二倍的方法,所以就算最后一层没有完全占用,依旧要开上它的空间。
建树
在输入原数组后,就可以先建树了,建完树后进行一些区间的维护也方便。
建树是从根节点开始的,层层向下递归,直到遇到叶子节点后保存叶子节点信息,再向上回溯维护信息。
void build(int p, int l, int r){
tree[p].l = l, tree[p].r = r;
if(l == r){ //遇到叶子节点
tree[p].dat = a[l];
return;
}
int mid = l + r >> 1;
build(p * 2, l, mid); //建左子树
build(p * 2 + 1, mid + 1, r); //建右子树
tree[p].dat = tree[p * 2].dat + tree[p * 2 + 1].dat; //维护信息
}
//调用:
build(1, 1, n);
单点修改与区间查询
区间修改
需要用到一个懒惰标记,这样就不用每次修改都把值传下去,而是在后续操作中遇到标记再下传。
#include <bits/stdc++.h>
#define maxn 100000
#define int long long
using namespace std;
int m,n;
#define ls k << 1
#define rs k << 1 | 1
#define mid (l + r >> 1)
int tree[maxn << 2], tag[maxn << 2];
void pushup(int k) {
tree[k] = tree[ls] + tree[rs];
}
void Pushup(int k) {
tree[k] = tree[ls] + tree[rs];
}
void Build(int k, int l, int r) {
if (l == r) {
cin >> tree[k];
return;
}
Build(ls, l, mid);
Build(rs, mid + 1, r);
pushup(k);
}
void Add(int k, int l, int r, int v) {
tag[k] += v;
tree[k] += 1ll * (r - l + 1) * v;
}
void pushdown(int k, int l, int r) {
if (!tag[k]) return;
Add(ls, l, mid, tag[k]);
Add(rs, mid + 1, r, tag[k]);
tag[k] = 0;
}
void Modify(int k, int l, int r, int x, int y, int v) {
if (l >= x && r <= y) return Add(k, l, r, v);
pushdown(k, l, r);
if (x <= mid) Modify(ls, l, mid, x, y, v);
if (mid < y) Modify(rs, mid + 1, r, x, y, v);
pushup(k);
}
int Query(int k, int l, int r, int x, int y) {
if (l >= x && r <= y) return tree[k];
pushdown(k, l, r);
int ret = 0;
if (x <= mid) ret += Query(ls, l, mid, x, y);
if (mid < y) ret += Query(rs, mid + 1, r, x, y);
return ret;
}
signed main() {
cin >> n >> m;
Build(1, 1, n);
for (int i = 1, opt, x, y, z; i <= m; i++) {
cin >> opt >> x >> y;
if (opt == 1) {
cin >> z;
Modify(1, 1, n, x, y, z);
}
if(opt == 2){
cout<<Query(1, 1, n, x, y)<<endl;
}
}
return 0;
}
区间乘法:需要维护两个懒惰标记,一个加一个乘,在下传时要注意顺序。
#include<bits/stdc++.h>
#define maxn 100005
#define int long long
using namespace std;
int n, m, mod;
int a[maxn];
struct node{
int l, r, tag1, tag2, sum;
}t[4*maxn];
void build(int p, int l, int r){
t[p].l = l, t[p].r = r, t[p].tag2 = 1;
if(l == r){
t[p].sum = a[l]%mod;
return;
}
int mid = l + r >> 1;
build(p*2, l, mid);
build(p*2+1, mid + 1, r);
t[p].sum = (t[p*2].sum + t[p*2+1].sum) %mod;
}
void spread(int p){
t[p*2].sum = (t[p].tag2 * t[p*2].sum + (t[p*2].r - t[p*2].l + 1) * t[p].tag1)%mod ;
t[p*2+1].sum = (t[p].tag2 * t[p*2+1].sum + (t[p].tag1 * (t[p*2+1].r - t[p*2+1].l + 1)) )%mod ;
t[p*2].tag2 = (t[p*2].tag2 * t[p].tag2)%mod ;
t[p*2+1].tag2 = (t[p*2+1].tag2 * t[p].tag2)%mod ;
t[p*2].tag1 = (t[p*2].tag1 * t[p].tag2 + t[p].tag1)%mod ;
t[p*2+1].tag1 = (t[p*2+1].tag1 * t[p].tag2 + t[p].tag1) %mod;
t[p].tag2 = 1;
t[p].tag1 = 0;
}
void add(int p, int x, int y, int k){
if(x <= t[p].l && y >= t[p].r){
t[p].sum = (t[p].sum + k * (t[p].r - t[p].l + 1)) % mod;
t[p].tag1 = (t[p].tag1 + k)%mod ;
return;
}
spread(p);
t[p].sum = (t[p*2].sum + t[p*2+1].sum) ;
int mid = t[p].l + t[p].r >> 1;
if(x <= mid) add(p*2, x, y, k);
if(y > mid) add(p*2+1, x, y, k);
t[p].sum = (t[p*2].sum + t[p*2+1].sum) ;
}
void mul(int p,int x,int y,int k){
if(t[p].l>=x && t[p].r<=y){
t[p].tag1 = (t[p].tag1 * k) ;
t[p].tag2 = (t[p].tag2 * k) ;
t[p].sum = (t[p].sum * k) ;
return ;
}
spread(p);
t[p].sum = t[p*2].sum + t[p*2+1].sum;
int mid = (t[p].l + t[p].r) >> 1;
if(x <= mid) mul(p*2, x, y, k);
if(mid < y) mul(p*2+1, x, y, k);
t[p].sum = (t[p*2].sum + t[p*2+1].sum)%mod;
}
int ask(int p, int x, int y){
if(t[p].l >= x && t[p].r <= y){
return t[p].sum;
}
spread(p);
int as=0;
int mid = (t[p].l+t[p].r)>>1;
if(x <= mid) as = (as + ask(p*2, x, y))%mod ;
if(mid < y) as = (as + ask(p*2+1, x, y))%mod ;
return as;
}
signed main(){
cin >> n >> m >> mod;
for(int i = 1; i <= n; i++) cin >> a[i];
build(1, 1, n);
for(int i = 1, opt, x, y, k; i <= m; i++){
cin >> opt;
if(opt == 1){
cin >> x >> y >> k;
mul(1, x, y, k);
}
if(opt == 2){
cin >> x >> y >> k;
add(1, x, y, k);
}
if(opt == 3){
cin >> x >>y;
cout << ask(1, x, y)%mod << endl;
}
}
return 0;
}
线段树应用
扫描线
权值线段树
所谓权值线段树就是在值域上建一棵线段树,当插入一个数时,其位置加一。
优化:动态开点
我们可以看到,在值域上开一棵线段树是非常危险的,这很可能会爆空间
可持久化线段树
可持久化线段树即为可保存历史版本的线段树。
在一个历史版本上修改时,只用新建被修改了的节点,没有修改的节点直接指向原来的历史版本就行。
根节点仍然是调用这棵树的入口,会有很多根节点,每一个根节点都是其所在的历史版本的入口。
可持久化数组
模板:P3919 【模板】可持久化线段树 1(可持久化数组)
#include <bits/stdc++.h>
#define maxn 1000012
using namespace std;
struct node{
int lc, rc, dat;
}t[30*maxn];
int root[maxn], tot;
int n, m, a[maxn], cnt;
inline int read(){
int f=1,x=0;char ch;
do{ch=getchar();if(ch=='-')f=-1;}while(ch<'0'||ch>'9');
do{x=x*10+ch-'0';ch=getchar();}while(ch>='0'&&ch<='9');
return f*x;
}
int build(int l, int r){
int p = ++tot;
if(l == r){
t[p].dat = a[l];
return p;
}
int mid = (l + r) >> 1;
t[p].lc = build(l, mid);
t[p].rc = build(mid + 1, r);
t[p].dat = max(t[t[p].lc].dat , t[t[p].rc].dat);
return p;
}
int change(int now, int l, int r, int x, int val){
int p = ++tot;
t[p] = t[now];
if(l == r){
t[p].dat = val;
return p;
}
int mid = (l + r) >> 1;
if(x <= mid) t[p].lc = change(t[now].lc, l, mid, x, val);
else t[p].rc = change(t[now].rc, mid+1, r, x, val);
t[p].dat = max(t[t[p].lc].dat , t[t[p].rc].dat);
return p;
}
int query(int p, int l, int r, int x){
if (l == r) return t[p].dat;
int mid = (l + r) >> 1;
if (x <= mid) return query(t[p].lc, l, mid, x);
else return query(t[p].rc, mid + 1, r, x);
}
signed main(){
n = read(), m = read();
for(int i = 1; i <= n; i++) a[i] = read();
root[0] = build(1, n);
for(int i = 1, now, opt, x, val; i <= m; i++){
now = read(), opt = read();
if(opt == 1){
x = read(), val = read();
root[i] = change(root[now], 1, n, x, val);
}
if(opt == 2){
x = read();
cout << query(root[now], 1, n, x) <<endl;
root[i] = root[now];
}
}
}
可持久化权值线段树(主席树)
主席树板子:静态区间第k小
#include <bits/stdc++.h>
#define maxn 200005
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int n, m, p, q;
int lc[maxn << 6], rc[maxn << 6], sum[maxn << 6], rt[maxn << 6];
int a[maxn << 6], b[maxn << 6];
int node_cnt;
void build(int &t, int l, int r) {
t = ++node_cnt;
if(l == r) return;
int mid = (l + r) >> 1;
build(lc[t], l, mid);
build(rc[t], mid + 1, r);
}
int modify(int o, int l, int r) {
int oo = ++node_cnt;
lc[oo] = lc[o], rc[oo] = rc[o], sum[oo] = sum[o] + 1;
if (l == r) return oo;
int mid = l + r >> 1;
if (p <= mid) lc[oo] = modify(lc[oo], l, mid);
else rc[oo] = modify(rc[oo], mid + 1, r);
return oo;
}
int query(int u, int v, int l, int r, int k) {
int x = sum[lc[v]] - sum[lc[u]];
if (l == r) return l;
int mid = l + r >> 1;
int ans;
if (x >= k) ans = query(lc[u], lc[v], l, mid, k);
else ans = query(rc[u], rc[v], mid + 1, r, k - x);
return ans;
}
int main() {
n = read(), m = read();
for (int i = 1; i <= n; i++) a[i] = read(), b[i] = a[i];
sort(b + 1, b + n + 1);
q = unique(b + 1, b + n + 1) - b - 1;
build(rt[0], 1, q);
for (int i = 1; i <= n; i++) {
p = lower_bound(b + 1, b + q + 1, a[i]) - b;
rt[i] = modify(rt[i - 1], 1, q);
}
while (m--) {
int l = read(), r = read(), k = read();
int tmp = query(rt[l - 1], rt[r], 1, q, k);
cout << b[tmp] << endl;
}
}
其他例题:
大慈善家
大慈善家
题目背景
大家都知道,\(lsy\) 除了是 \(JY\) 中学的学生之外,还是一名大大大大大——大慈善家(手动鬼畜)。因为 \(JY\) 的机房十分的好啊(咳咳),所以 \(lsy\) 就决定在假期大干一场——做慈善,毕竟有许多的地方还没有像 \(JY\) 一样的大机房,所以 \(lsy\) 勤勤恳恳地攒了许多的软妹币,决定进行慈善。
\(lsy\) 将目光放在了一条街上,在这个街上是没有机房的(多么可怕)所以 \(lsy\) 决定从机房开始入手,但为了展现 \(JY\) 学子的风范, \(lsy\) 决定将电脑排成一排,(显得财大气粗),但很明显一排是远远不够的,所以 \(lsy\) 大笔一挥“我要 \(n\) 排!”\(xing\) 不禁为他的这种精神感动,但看着已经高度赤字的经费,“\(lsy\) 啊,这要是全是电脑的话,会被踢插排的!(鞭尸)”\(lsy\) 略微沉思,于是修改了策略,只在 \(l_i\) , \(r_i\) ,作为两个端点来修建电脑,但还是要 \(n\) 排!
现在大功告成,\(lsy\) 十分欣赏自己的杰作,随口说了一句“要是 \(X\) 老师也在这里的话,那该有多好啊!”但因$ xing$ 把工作扔掉一边,所以 \(lsy\) 根本不知道到底怎么建的电脑,所以他看了看屏幕前的你,喂!不要再笑了,听着!接下来你的任务就是帮 \(xing\) 统计一下完全在区间 \([L , R]\) 上的电脑有多少排。
当然,\(lsy\) 不止于此,所以他会有 \(q\) 的问题,但\(xing\) 显然是不太行啊,所以就靠你了!
题目描述
\(n\) 条线段,每条线段的端点为 \(l_i\,,r_i\) ,\(q\) 次询问完全在区间 \([L,R]\) 的线段有多少个。
输入格式
第一行两个个整数 \(n\,,q\) ,代表线段个数和询问的个数。
接下来 \(n\) 行,每行两个整数 \(l_i\,,r_i\) ,表示第 \(i\) 条线段的端点坐标。
接下来 \(q\) 行,每行两个整数 \(L\,,R\) ,\([L\,\&\,ans + 1,R\,|\,ans + 1]\)表示询问的区间。(\(p.s.\ ans\) 表示上一次的答案,初始时 \(ans = 0\))
输出格式
对于每个询问,一个整数表示完全在区间内的线段个数。
样例 #1
样例输入 #1
6 2 1 5 3 5 4 7 5 9 1 3 2 4 1 5 6 10样例输出 #1
4 1提示
完全在区间内指 \(L \le l_i , r_i \le R\) 。
\(30\%\) 的数据满足 \(l_i < r_i \le 10^5\) ,\(n,q \le 3000\) 。
另外 \(20\%\) 的数据满足 \(l_i\) 的不同取值不超过 \(10\) 个。
\(100\%\) 的数据满足 \(l_i < r_i \le 10^9\) ,\(n,q \le 2 \times 10^5\) 。
时限与空间均已开到 \(std\) 的五倍以上。
特别鸣谢
Tips
1.标记永久化
标记永久化就少了每次都上传下传,常数会小很多。
标记永久化的原理简单来说就是修改时一路更改被影响到的点,询问时则一路累加路上的标记,从而省去下传标记的操作。
//以下抄自标记永久化 - wozaixuexi - 博客园 (cnblogs.com)
3.0 说明
这里以区间修改区间求和的线段树为例。
线段树中编号为p的结点的值和标记分别为val[p]和mark[p]。
3.1 建树
标记永久化线段树的建树和标记不永久化线段树的建树没有什么区别,这里就不在赘述,直接上代码吧。
void Build(int p,int l,int r)
{
if(l==r) {scanf("%lld",&val[p]);return;}
int mid=(l+r)>>1;
Build(p<<1,l,mid);//递归建左子树
Build(p<<1|1,mid+1,r);//递归建右子树
val[p]=val[p<<1]+val[p<<1|1];//这里是要向上更新一下的
}
3.2 区间修改
0.设要将区间[xy]中的数都加上v。
1.一路走下去同时更新路上受此次修改影响的节点的值,即val[p]+=(y-x+1)*v。
2.当目前结点所代表的区间与待修改区间完全重合时,更新标记,返回,即mark[p]+=v;
void add(int p,int l,int r,int x,int y,long long v)
{
val[p]+=(y-x+1)*v;//更新该结点的权值
if(l==x&&r==y) {mark[p]+=v;return;}//更新标记
int mid=(l+r)>>1;
if(y<=mid) add(p<<1,l,mid,x,y,v);
else if(x>mid) add(p<<1|1,mid+1,r,x,y,v);
else add(p<<1,l,mid,x,mid,v),add(p<<1|1,mid+1,r,mid+1,y,v);
}
有人可能会问:标记更新后直接返回的话下面的结点不就没更新了吗?
慢慢来嘛,往下看就明白啦。
3.3 区间询问
0.设要要区间[x,y]中的数的总和。
1.一路走下去同时累加路上的标记,因为在修改操作中标记并没有下传,所以要这样子,即ad+=mark[p]。
2.当目前结点所代表的区间与待修改区间完全重合时,返回当前结点的值与累加下来的标记乘上询问区间长度的和,即return val[p]+(y-x+1)*ad。
int ask(int p,int l,int r,int x,int y,int ad)//ad为一路上累加的标记
{
if(l==x&&r==y) return val[p]+(y-x+1)*ad;
int mid=(l+r)>>1;
if(y<=mid) return ask(p<<1,l,mid,x,y,ad+mark[p]);
if(x>mid) return ask(p<<1|1,mid+1,r,x,y,ad+mark[p]);
return ask(p<<1,l,mid,x,mid,ad+mark[p])+ask(p<<1|1,mid+1,r,mid+1,y,ad+mark[p]);
}
2.非递归进行线段树的操作 —— ZKW 线段树。
平衡树
Treap
Treap 是一种 弱平衡 的 二叉搜索树。它的数据结构由二叉树和二叉堆组合形成,名字也因此为 tree 和 heap 的组合。
Treap 的每个结点上除了按照二叉搜索树排序的 \(key\) 值外要额外储存一个叫 \(property\) 的值。它由每个结点建立时随机生成,并按照 最大堆 性质排序。因此 treap 除了要满足二叉搜索树的性质之外,还需满足父节点的 \(property\) 大于等于两个子节点的值。所以它是 期望平衡 的。搜索,插入和删除操作的期望时间复杂度为 \(O(logn)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int SIZE = 1000000;
struct treap{
int l,r;
int val,dat;
int cnt,size;
}a[SIZE];
int tot,root,n,INF=1e9;
int New(int val){
a[++tot].val=val;
a[tot].dat=rand();
a[tot].cnt=a[tot].size=1;
return tot;
}
void update(int p){
a[p].size=a[a[p].l].size+a[a[p].r].size+a[p].cnt;
}
void build(){
New(-INF),New(INF);
root=1,a[1].r=2;
update(root);
}
int getrbyv(int p,int val){
if(p==0)return 0;
if(val==a[p].val)return a[a[p].l].size+1;
if(val<a[p].val)return getrbyv(a[p].l,val);
return getrbyv(a[p].r,val)+a[a[p].l].size+a[p].cnt;
}
int getvbyr(int p,int rank){
if(p==0)return INF;
if(a[a[p].l].size>=rank)return getvbyr(a[p].l,rank);
if(a[a[p].l].size+a[p].cnt>=rank)return a[p].val;
return getvbyr(a[p].r,rank-a[a[p].l].size-a[p].cnt);
}
void zig(int &p){
int q=a[p].l;
a[p].l=a[q].r,a[q].r=p,p=q;
update(a[p].r),update(p);
}
void zag(int &p){
int q=a[p].r;
a[p].r=a[q].l,a[q].l=p,p=q;
update(a[p].l),update(p);
}
void insert(int &p,int val){
if(p==0){
p=New(val);
return;
}
if(val==a[p].val){
a[p].cnt++,update(p);
return ;
}
if(val<a[p].val){
insert(a[p].l,val);
if(a[p].dat<a[a[p].l].dat)zig(p);
}
else{
insert(a[p].r,val);
if(a[p].dat<a[a[p].r].dat)zag(p);
}
update(p);
}
int getpre(int val){
int ans=1;
int p=root;
while(p){
if(val==a[p].val){
if(a[p].l>0){
p=a[p].l;
while(a[p].r>0)p=a[p].r;
ans=p;
}
break;
}
if(a[p].val<val&&a[p].val>a[ans].val)ans=p;
p=val<a[p].val?a[p].l:a[p].r;
}
return a[ans].val;
}
int getnext(int val){
int ans=2;
int p=root;
while(p){
if(val==a[p].val){
if(a[p].r>0){
p=a[p].r;
while(a[p].l>0)p=a[p].l;
ans=p;
}
break;
}
if(a[p].val>val&&a[p].val<a[ans].val) ans=p;
p=val<a[p].val?a[p].l:a[p].r;
}
return a[ans].val;
}
void remove(int &p,int val){
if(p==0)return ;
if(val==a[p].val){
if(a[p].cnt>1){
a[p].cnt--,update(p);
return ;
}
if(a[p].l||a[p].r){
if(a[p].r==0||a[a[p].l].dat>a[a[p].r].dat)
zig(p),remove(a[p].r,val);
else
zag(p),remove(a[p].l,val);
update(p);
}
else p=0;
return ;
}
if(val<a[p].val)remove(a[p].l,val);
else remove(a[p].r,val);
update(p);
}
signed main(){
build();
cin>>n;
while(n--){
int opt,x;
cin>>opt>>x;
switch(opt){
case 1: insert(root,x); break;
case 2: remove(root,x); break;
case 3:cout<<getrbyv(root,x)-1<<endl;break;
case 4:cout<<getvbyr(root,x+1)<<endl;break;
case 5:cout<<getpre(x)<<endl;break;
case 6:cout<<getnext(x)<<endl;break;
}
}
return 0;
}
笛卡尔树
笛卡尔树是一种二叉树,每一个结点由一个键值二元组 构成。要求 满足二叉搜索树的性质,而 满足堆的性质。一个有趣的事实是,如果笛卡尔树的 键值确定,且 互不相同, 互不相同,那么这个笛卡尔树的结构是唯一的。上图:
上面这棵笛卡尔树相当于把数组元素值当作键值 ,而把数组下标当作键值 。显然可以发现,这棵树的键值 满足二叉搜索树的性质,而键值 满足小根堆的性质。
其实图中的笛卡尔树是一种特殊的情况,因为二元组的键值 恰好对应数组下标,这种特殊的笛卡尔树有一个性质,就是一棵子树内的下标是连续的一个区间(这样才能满足二叉搜索树的性质)。更一般的情况则是任意二元组构建的笛卡尔树。
如下图建树:
#include <bits/stdc++.h>
#define maxn 10000005
using namespace std;
int a[maxn], n;
struct tree{
int lc, rc, v;
}t[maxn];
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int main(){
n = read();
int cnt = 0;
int pos = 0;
for(int i = 1; i <= n; i++){
a[i] = read();
pos = cnt;
while(pos && a[t[pos].v] > a[i]) pos --;
if(pos) t[t[pos].v].rc = i;
if(pos < cnt) t[i].lc = t[pos + 1].v;
t[cnt = ++pos].v = i;
}
long long L=0, R=0;
for(int i = 1; i <= n; i++){
L ^=1ll* i * (t[i].lc + 1);
R ^=1ll* i * (t[i].rc + 1);
}
cout << L << " " << R;
}
分块
块状链表
基本概念
块状链表本身是一个链表,但是链表储存的并不是一般的数据,而是由这些数据组成的顺序表。每一个块状链表的节点,也就是顺序表,可以被叫做一个块。
块状链表是基于分块思想设计的一种数据结构,其基本定应用为:把一个长度为n的串,分成约块,相邻两块的大小不小于 \(\sqrt n\),每一块的大小不超过 \(2\sqrt n\)。这样就可以在的时间内解决一个插入、询问、拆分、合并等等的操作。其时间复杂度比平衡树高,空间复杂度比平衡树低。
块状链表就是数组与链表的组合,我们先来回顾一下链表与数组基本操作的时间复杂度:
| 操作 | 数组 | 链表 |
|---|---|---|
| 存储结构 | 地址连续的存储单元,物理位置相邻 | 地址不连续,物理位置不相邻 |
| 定位 | \(O(1)\) | \(O(n)\) |
| 插入 | \(O(n)\) | \(O(1)\) |
| 删除 | \(O(n)\) | \(O(1)\) |
可以发现,数组定位效率较高,但插入删除效率低;链表插入删除效率高,但由于地址不连续,定位效率低。两者各有优缺点。
对于一个要求实现定位、插入、删除的数据结构,用平衡树实现过于复杂,我们想办法设计一个兼有数组和链表性质的数据结构,也就是 块状链表。块状链表中的节点是一个个数组,我们将整个序列分为 \(\sqrt n\) 个节点,每个节点数组的大小为 \(\sqrt n\),这样保证定位和插入删除的复杂度都约为 \(O(\sqrt n)\)。
大概长这个样子:(从csdn上捞的图
实现
一个块状链表至少要支持的操作有 定位、插入、删除 等,在实现过程中,为了维持节点数量,还需要用到 合并 操作,在实现插入、删除过程中会用到 分裂 操作。
实际实现有两种,第一种是把数组作为链表的元素,第二种是把数组分块后每一块都用小链表维护,然后个小链表再用一个大链表串起来。
个人觉得第一种就足够了,不太理解每一块用小链表维护的必要性,下面将以第一种实现为例。如果有的题需要第二种实现可以看这位大佬的博客。
我们以这道题为例讲解一下具体的实现过程。
构建
定义一个结构体,储存数组、数组大小、左节点、右节点等信息。
struct node {
char s[2005];
int c, l, r;
}p[maxn];
这道题没有给定初始数组,如果给定了初始数组,可以先将初始数组加入链表。
定位
在这道题中相当于 Move 操作。假设我们要定位到 \(k\),那么我们可以利用保存的节点大小找到这个位置在的那一块,然后根据数组下标定位。故而可以将 \(k\) 的“坐标”设为 \((x, y)\),用来表示在哪个节点的哪个位置。
void move(int k) {
x = p[0].r;
while (k > p[x].c) k -= p[x].c, x = p[x].r;
y = k - 1;
}
对于 Prev 操作和 Next 操作,只需判断是否在块内的情况即可。
void pre() {
if (!y) x = p[x].l, y = p[x].c - 1;
else y--;
}
void nxt() {
if (y < p[x].c - 1) y++;
else x = p[x].r, y = 0;
}
插入
分为两种情况。
添加区间在两个块之间
对于插入的区间新建区块存储(可能是多个),然后接到原链表上。
添加区间在一个块内
首先要将所要插入到的那个区块从插入位置断开:

然后就是和第一种情况一样地,将待插入区间新建区块,插入原链表
再看具体实现,对于断区间的操作,我们可以新建一个节点,复制断点后的全部信息,再在原先节点删去断点后的信息,时间复杂度 \(O(\sqrt n)\);对于将新区间插入的操作,每 \(\sqrt n\) 长度新建一个区块,最坏情况要新建 \(\sqrt n\) 个区块,时间复杂度也是 \(O(\sqrt n)\)。
Code:
//insert k ch
void insert(int k) {
//cur in node -->split
if (y < p[x].c - 1) {
int u = q[tot--];
for (int i = y + 1; i < p[x].c; i++)
p[u].s[p[u].c++] = p[x].s[i];
p[x].c = y + 1;
add(x, u);
}
//creat and insert new nodes
int cur = x;
for (int i = 0; i < k;) {
int u = q[tot--];
while (p[u].c < 2005 && i < k)
p[u].s[p[u].c++] = str[i++];
add(cur, u);
cur = u;
}
}
其中,对于 \(add\) 函数:
//add v to u's right
void add(int u, int v) {
p[v].r = p[u].r, p[p[v].r].l = v;
p[u].r = v, p[v].l = u;
}
删除
依旧是分为两种情况:
删除区间在一个区块内
这种情况好说,只需动一动这个区块的数组下标和元素个数总数就行了。
if (p[x].c - 1 - y >= k) {
for (int i = y + k + 1, j = y + 1; i < p[x].c; i++, j++)
p[x].s[j] = p[x].s[i];
p[x].c -= k;
}
删除区间跨越区块
需要分别删除开头区块的后半段区间、结尾区块的前半段区间和中间的整块节点。前两个好说,方法同第一种情况,下面主要说整块节点的删除。
我们回想一下之前链表删除节点,就是断绝被删节点与周围节点的关系:

对于块状链表的节点,我们显然也可以这么办。但是有一个新的问题产生了:对于我们删掉的节点,它的节点编号是被永远占用的,换句话说,它永远要占一部分内存,这就有可能在添加区间时增加的节点无处可放,超出内存限制。
所以我们要用到一种 内存回收 的技巧来优化。也就是上文插入操作的代码中的 \(q\) 数组和 \(tot\)。我们在一开始就先将 \(q(i)\) 初始为 \(i\),\(tot\) 初始为 最大节点数量,相当于是构建了一个栈,在增加节点时就去除栈顶元素作为编号,在删除节点时就将其编号重新放入栈中表示已经没有有用信息使用这个节点了,可以占用这个编号。这也体现了链表存储的非连续性。
Code:
void delet(int u) {
p[p[u].l].r = p[u].r;
p[p[u].r].l = p[u].l;
p[u].l = p[u].r = p[u].c = 0;
q[++tot] = u; //内存回收
}
void remove(int k) {
if (p[x].c - 1 - y >= k) {
for (int i = y + k + 1, j = y + 1; i < p[x].c; i++, j++)
p[x].s[j] = p[x].s[i];
p[x].c -= k;
}
else {
k -= p[x].c - y - 1;
p[x].c = y + 1;
while (p[x].r && k >= p[p[x].r].c) {
int u = p[x].r;
k -= p[u].c;
delet(u);
}
int u = p[x].r;
for (int i = 0, j = k; j < p[u].c; i++, j++)
p[u].s[i] = p[u].s[j];
p[u].c -= k;
}
}
合并——保持平衡
如同平衡树的旋转一样,块状链表的合并也是保持“平衡”的一种手段。块状链表实际上就是将数组与链表结合,达到定位与插入删除的平衡,合并操作也是在维护这种平衡。
在上文提到的插入操作和删除操作中,可能会产生许多区块长度远小于 \(\sqrt n\) 的区块,这会大大降低块状链表的效率。所以我们在一定频率内,扫描一次整个链表,如果发现有相邻两个区块长度加起来还小于 \(\sqrt n\),就将它们合并为一个区块。时间复杂度约 \(O(\sqrt n)\)。
void merge() {
for (int i = p[0].r; i; i = p[i].r) {
while (p[i].r && p[i].c + p[p[i].r].c < 2005) {
int r = p[i].r;
for (int j = p[i].c, k = 0; k < p[r].c; j++, k++)
p[i].s[j] = p[r].s[k];
if (x == r) x = i, y += p[i].c;
p[i].c += p[r].c;
delet(r);
}
}
}
查询
查询操作其实就很简单了~依旧是分在一个区块和多个区块两种情况。
void get(int k) {
if (p[x].c - 1 - y >= k) {
for (int i = 0, j = y + 1; i < k; i++, j++)
cout << p[x].s[j];
}
else {
k -= p[x].c - y - 1;
for (int i = y + 1; i < p[x].c; i++)
cout << p[x].s[i];
int cur = x;
while (p[cur].r && k >= p[p[cur].r].c) {
int u = p[cur].r;
for (int i = 0; i < p[u].c; i++) cout << p[u].s[i];
k -= p[u].c;
cur = u;
}
int u = p[cur].r;
for (int i = 0; i < k; i ++ ) cout << p[u].s[i];
}
cout << endl;
}
#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
inline int read() {
int x = 0, f = 1; char c = getchar();
while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
struct node {
char s[2005];
int c, l, r;
// 一个块 :0~c
}p[2005];
char str[2000005];
int q[2005], tot;
int n, x, y; // x: 第几个节点 y: 节点中第几个位置
void move(int k) {
x = p[0].r;
while (k > p[x].c) k -= p[x].c, x = p[x].r;
y = k - 1;
}
void pre() {
if (!y) x = p[x].l, y = p[x].c - 1;
else y--;
}
void nxt() {
if (y < p[x].c - 1) y++;
else x = p[x].r, y = 0;
}
//add v to u's right
void add(int u, int v) {
p[v].r = p[u].r, p[p[v].r].l = v;
p[u].r = v, p[v].l = u;
}
void delet(int u) {
p[p[u].l].r = p[u].r;
p[p[u].r].l = p[u].l;
p[u].l = p[u].r = p[u].c = 0;
q[++tot] = u; //内存回收
}
//insert k ch
void insert(int k) {
//cur in node -->split
if (y < p[x].c - 1) {
int u = q[tot--];
for (int i = y + 1; i < p[x].c; i++)
p[u].s[p[u].c++] = p[x].s[i];
p[x].c = y + 1;
add(x, u);
}
//creat and insert new nodes
int cur = x;
for (int i = 0; i < k;) {
int u = q[tot--];
while (p[u].c < 2005 && i < k)
p[u].s[p[u].c++] = str[i++];
add(cur, u);
cur = u;
}
}
void remove(int k) {
if (p[x].c - 1 - y >= k) {
for (int i = y + k + 1, j = y + 1; i < p[x].c; i++, j++)
p[x].s[j] = p[x].s[i];
p[x].c -= k;
}
else {
k -= p[x].c - y - 1;
p[x].c = y + 1;
while (p[x].r && k >= p[p[x].r].c) {
int u = p[x].r;
k -= p[u].c;
delet(u);
}
int u = p[x].r;
for (int i = 0, j = k; j < p[u].c; i++, j++)
p[u].s[i] = p[u].s[j];
p[u].c -= k;
}
}
void get(int k) {
if (p[x].c - 1 - y >= k) {
for (int i = 0, j = y + 1; i < k; i++, j++)
cout << p[x].s[j];
}
else {
k -= p[x].c - y - 1;
for (int i = y + 1; i < p[x].c; i++)
cout << p[x].s[i];
int cur = x;
while (p[cur].r && k >= p[p[cur].r].c) {
int u = p[cur].r;
for (int i = 0; i < p[u].c; i++) cout << p[u].s[i];
k -= p[u].c;
cur = u;
}
int u = p[cur].r;
for (int i = 0; i < k; i ++ ) cout << p[u].s[i];
}
cout << endl;
}
void merge() {
for (int i = p[0].r; i; i = p[i].r) {
while (p[i].r && p[i].c + p[p[i].r].c < 2005) {
int r = p[i].r;
for (int j = p[i].c, k = 0; k < p[r].c; j++, k++)
p[i].s[j] = p[r].s[k];
if (x == r) x = i, y += p[i].c;
p[i].c += p[r].c;
delet(r);
}
}
}
signed main() {
for (int i = 1; i < 2005; i++) q[++tot] = i;
n = read();
char opt[15];
str[0] = '%';
insert(1); move(1);
while (n--) {
cin >> opt;
if (!strcmp(opt, "Move")) {
int a = read();
move(a + 1);
}
if (!strcmp(opt, "Insert")) {
// int k = read();
// for (int i = 0; i < k;) {
// cin >> str[i];
// if (str[i] >= 32 && str[i] <= 126) i++;
// }
int a;
scanf("%d", &a);
int i = 0, k = a;
while (a)
{
str[i] = getchar();
if (str[i] >= 32 && str[i] <= 126) i ++, a -- ;
}
insert(k);
merge();
}
if (!strcmp(opt, "Delete")) {
int a = read();
remove(a);
merge();
}
if (!strcmp(opt, "Get")) {
int a = read();
get(a);
}
if (!strcmp(opt, "Prev")) pre();
if (!strcmp(opt, "Next")) nxt();
}
}
树状数组
树状数组是一个简单,常数小,实用的数据结构,但其维护的信息比较简单,结构不如线段树完全。
基本操作
void add(int x, int k) {
while (x <= n) { // 不能越界
c[x] = c[x] + k;
x = x + lowbit(x);
}
}
int getsum(int x) { // a[1]..a[x]的和
int ans = 0;
while (x >= 1) {
ans = ans + c[x];
x = x - lowbit(x);
}
return ans;
}
二维树状数组
void add(int x, int y, int k) {
while (x <= n) {
int ty = y;
while (ty <= n)
c[x][ty] += k, ty += lowbit(ty);
x = x + lowbit(x);
}
}
int getsum(int x, int y) {
int ans = 0;
while (x >= 1) {
int ty = y;
while (ty)
ans += c[x][ty], ty -= lowbit(ty);
x = x - lowbit(x);
}
return ans;
}
矩形数点
#include <bits/stdc++.h>
#define maxn 600005
using namespace std;
#define int long long
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int n, m;
int tc[20 * maxn], ans[maxn][10];
struct node{
int x, y, id;
}t[4 * maxn];
int cnt;
int tot[maxn];
int b[4 * maxn];
bool cmp(node a, node b){
if(a.x != b.x) return a.x < b.x;
if(a.y != b.y) return a.y < b.y;
return a.id < b.id;
}
inline void add(int x, int y){
while(x <= maxn){
tc[x] += y;
x += x & -x;
}
}
inline int query(int x){
int ans = 0;
while(x){
ans += tc[x];
x -= x & -x;
}
return ans;
}
signed main(){
n = read(), m = read();
for(int i = 1; i <= n; i++) {
t[i].x = read(), t[i].y = read();
t[i].id = 0;
}
cnt = n;
for(int i = 1; i <= m; i++) {
int a = read(), b = read(), c = read(), d = read();
t[++cnt].x = a - 1, t[cnt].y = b - 1, t[cnt].id = i;
t[++cnt].x = a - 1, t[cnt].y = d, t[cnt].id = i;
t[++cnt].x = c, t[cnt].y = b - 1, t[cnt].id = i;
t[++cnt].x = c, t[cnt].y = d, t[cnt].id = i;
}
sort(t + 1, t + cnt + 1, cmp);
for(int i = 1; i <= cnt; i++) b[i] = t[i].y;
sort(b + 1, b + 1 + cnt);
int ed = unique(b + 1, b + 1 + cnt) - b - 1;
for(int i = 1; i <= cnt; i++) {
int tmp = lower_bound(b + 1, b + ed + 1, t[i].y) - b;
if(t[i].id) ans[t[i].id][++tot[t[i].id]] += query(tmp);
if(!t[i].id) add(tmp, 1);
}
for(int i = 1; i <= m; i++)
cout << ans[i][4] - ans[i][3] - ans[i][2] + ans[i][1] << endl;
}
树状数组上二分
树状数组上二分是一个较为冷门的树状数组应用。其过程类似于倍增,令 j 从 log n 到 0 进行循环,如果可 以将当前长度增加 2 j 就增加。最终长度就是结果。由于 树状数组的性质,判断能否将当前长度增加只需要访问一 个树状数组的元素即可
tips
- 将修改和查询的函数交换(\(+lowbit\) 与 \(-lowbit\) 互换),可以 看做维护后缀和。
- 树状数组的区间加区间和是比正常写法的线段树快很多的, 具体的写法可以看做两个树状数组,一个维护原数组,一个维护前缀和。
- 树状数组的一个小卡常,例如要在 \(x\) 处 \(+z\),\(y\) 处 \(−z\),可以 \(x, y\) 一起跳,每次跳小的一边,两个跳到同一位置就立刻退出, 实测很有效
字符串算法
字符串hash
字符串hash即为将字符串转化为一个数
一般\(base\)取一个质数(如131)
//luogu p3370
int n;
unsigned long long a[maxn];
signed main() {
n = read();
for (int i = 1; i <= n; i++) {
string s;
cin >> s;
int m = s.length();
unsigned long long res = 0;
for (int j = 0; j < m; j++) {
res = res * 131 + (unsigned long long)s[j];
}
a[i] = res;
}
sort(a + 1, a + n + 1);
int ans = 1;
for (int i = 2; i <= n; i++) if (a[i - 1] != a[i]) ans++;
cout << ans;
}
hash表
个人感觉跟链表很像?
KMP
近日,园长发现动物园中好吃懒做的动物越来越多了。例如企鹅,只会卖萌向游客要吃的。为了整治动物园的不良风气,让动物们凭自己的真才实学向游客要吃的,园长决定开设算法班,让动物们学习算法。
某天,园长给动物们讲解KMP算法。
园长:“对于一个字符串\(S\),它的长度为\(L\)。我们可以在\(O(L)\)的时间内,求出一个名为
next的数组。有谁预习了next数组的含义吗?”熊猫:“对于字符串\(S\)的前\(i\)个字符构成的子串,既是它的后缀又是它的前缀的字符串中(它本身除外),最长的长度记作\(next[i]\)。”
园长:“非常好!那你能举个例子吗?”
熊猫:“例\(S\)为
abcababc,则\(next[5]=2\)。因为\(S\)的前\(5\)个字符为abcab,ab既是它的后缀又是它的前缀,并且找不到一个更长的字符串满足这个性质。同理,还可得出\(next[1] = next[2] = next[3] = 0\),\(next[4] = next[6] = 1\),\(next[7] = 2\),\(next[8] = 3\)。”园长表扬了认真预习的熊猫同学。随后,他详细讲解了如何在\(O(L)\)的时间内求出
next数组。 ——选自[NOI2014] 动物园
在 KMP 算法中 $ nxt$ 数组的思想很重要,NOI2014的这道题中就说了 \(nxt\) 数组的含义。
为什么要有这个 \(nxt\) 数组呢?
想象一下暴力求字符串匹配:如果我要是遇到这种情况:
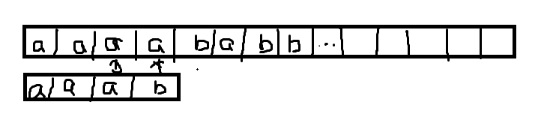
在第四个位置,不匹配了,怎么办,我只能推倒重来,让文本串的第二个位置尝试匹配模板串。
但是如果用了 \(nxt\) 数组呢?我直接让模板串向后移动一位找匹配就行。
因为目前既然已经匹配了这么多,前面的都是匹配的,那么我们就要尽可能的少的移动模板串,怎么尽可能少呢?移动到最长公共前缀是最少的。
#include <bits/stdc++.h>
const int MAXN = 1e6 + 10;
using namespace std;
char s1[MAXN], s2[MAXN];
int nxt[MAXN], l1,l2;
int main(){
scanf("%s%s",s1 + 1,s2 + 1);
int l1 = strlen(s1 + 1), l2 = strlen(s2 + 1);
nxt[1] = 0;
for (int i = 1, j = 0; i < l2; i++){
while(j > 0 && s2[j + 1] != s2[i + 1]) j = nxt[j];
if(s2[j + 1] == s2[i + 1]) j++;
nxt[i + 1] = j;
}
for (int i = 1, j = 0; i <= l1; i++){
while(j > 0 && s2[j + 1] != s1[i]) j = nxt[j];
if(s2[j + 1] == s1[i]) j++;
if(j == l2){
printf("%lld\n", i - l2 + 1);
j = nxt[j];
}
}
for (int i = 1; i <= l2; i++) printf("%lld ", nxt[i]);
return 0;
}
图论
图论概述
图
图结构是描述和解决实际应用问题的一种基本而有力的工具 ——《数据结构》
图的定义:所谓的图可定义为 \(G = (V, E)\) ,其中集合 \(V\) 中的元素叫做 节点(node),集合 \(E\) 中的元素叫做 边(edge)。每条边对应 \(V\) 集合中的一对节点 \((u, v)\) ,代表他们有一定的关系。
为了方便计算,\(V\) 和 \(E\) 都是有限集。
无向图、有向图以及混合图
可大致按照边有无方向将图分为无向图和有向图。
对于边集 \(E\) 中的元素 \((u, v)\),如果 \(u\) 和 \(v\) 的次序无所谓,则这样的图称为有向图,否则称为无向图,有时一张图中两者皆有,称为混合图。
其实不用考虑那么多,可以对于无向边双向建边,这样可以都转化为有向图。
度
对于一张图的每个节点,与其关联的边数称为度。
对于一条有向边 \((u, v)\) ,对于节点 \(u\) 的出度有 1 贡献,对于 \(v\) 的入度有 1 贡献。
简单图
简单图即为没有自环的图。自环即为两端连接同一节点的边。这类边可能确实有其独特意义,如在城市交通图中,但是一般不讨论自环,有一些题目的数据会出现自环,但这可能是数据随机生成的缘故,对于题目没什么影响,除非觉得存不下特判一下。
通路与回路
所谓通路,也就是路径,是 \(m + 1\) 个节点和 \(m\) 条边交替组成的序列。
\(\pi = \{v_0, e_1, v_1, e_2 ...v_m\}\)
对于任何 \(0 < i \le m\) ,\(e_i = (v_{i-1},v_i)\),也就是说序列中的节点依次首尾相连,其中沿途经过边的数量是 \(m\) ,记 \(|\pi| = m\)。
也可以简化描述,只列出节点:
\(\pi = \{v_0,v_1,v_2...v_m\}\)。
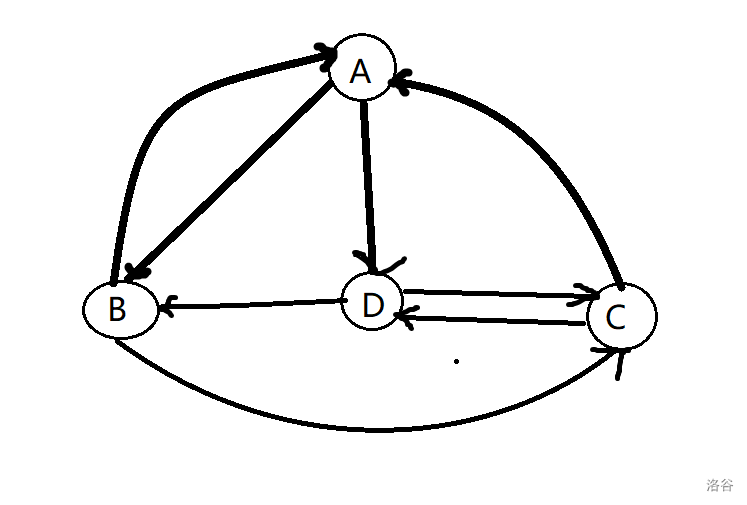
如上图,我们发现,尽管经过的边互不相同,但是经过的节点却可能有重复的。我们将沿途经过节点互异的通路称为简单通路,如下图。
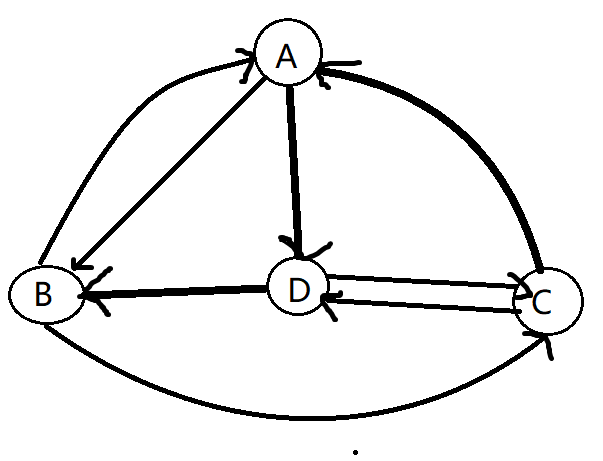
如果一条通路的起始节点和结束节点为同一个,则称为回路,其中,经过每条边恰好一次的回路称为欧拉回路
图的基础
概念
图论 (Graph theory) 是数学的一个分支,图是图论的主要研究对象。图 (Graph) 是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物间具有这种关系。 ——oi.wiki
图的存储
1.直接存边
直接存边多用于求最小生成树,它的优点就是可以排序,缺点则是时各边之间没有了连通性,也就是不能遍历。建图时,只需直接将这个边的起点、终点和边权即可:
struct edge{
int u, v, w;
}e[maxn];
输入时:
for(int i = 1; i <= n; i++){
int u, v, w;
cin >> u >> v >> w;
e[i].u = u, e[i].v = v, e[i].w = w;
}
2.邻接矩阵
也是存边的一种方法,建立一个二维数组,a[i][j]即表示从 i到 j有一条边,边权为 a[i][j] 。
int a[maxn][maxn];
for(int i = 1; i <= n; i++){
int u, v, w;
cin >> u >> v >> w;
a[u][v] = w;
//若为无向图,则要加上 a[v][u] = w;
}
但是我们可以看到,邻接矩阵是一个二维的,一旦数据过大就不适合使用了。另外,在遍历时要扫描每一个点和当前点有边,时间复杂度将是 \(O(n^2)\)。
3.邻接表
对于上述的邻接矩阵,有一种方法可以使其空间复杂度降低的方法,那就是邻接表,即用可变数组的方式存储图,e[i][j] = a 的意思即为i有一条连向a的边。
vector<int> e[maxn];
for(int i = 1, u, v; i <= m; i++){
cin >> u >> v;
e[u].push_back(v);
//无向图:e[v].push_back(u);
}
这样,一维固定,一维不固定,便大大节省了空间。
在遍历时,只需:
void dfs(int x){
vis[x] = 1;
for(int i = 0; i < e[x].size(); i++){
if(vis[e[x][i]]) continue;
dfs(e[x][i]);
}
}
遍历时间复杂度 \(O(n + m)\)
4.链式前向星
链式前向星是用数组的形式实现了一个静态链表。
struct edge{
int v, w, nxt;
}e[maxn];
int head[maxn], cnt;
void add(int u, int v, int w){
e[++cnt].v = v, e[cnt].w = w;
e[cnt].nxt = head[u], head[u] = cnt;
}
遍历:
void dfs(int x){
vis[x] = 1;
for(int i = head[x]; i; i = e[i].nxt){
if(vis[e[i].v]) continue;
dfs(e[i])
}
}
遍历时间复杂度 \(O(n)\)
最小生成树
概念
生成树:即在一个无向连通图中选几条边,使得这个这张图联通;
最小生成树 : 我们定义无向连通图的 最小生成树(Minimum Spanning Tree,MST)为边权和最小的生成树。
只有连通图才有生成树,对于不连通的图,只有生成生成森林。
Kruskal 算法
实现
Kruskal 算法的基本思想就是:对于一张图,按照边权的从小到大加入边,最后使得这张图连通。
Kruskal 算法的本质其实就是贪心策略,主要贪得是一下两方面:
- 将边权从小到大排序,先加入边权小的,一定不比先加入边权大的所生成的生成树大;
- 如果两个节点已经连通,那么不去加入连通这两个点的边一定比加入这个边所形成的生成树小;
基本实现过程如图:
代码
#include<bits/stdc++.h>
#define maxn 200005
using namespace std;
int n, m, as;
int f[maxn];
struct node{
int u, v, w;
}a[maxn];
bool cmp(node x, node y){
return x.w < y.w;
}
int find(int k){
if(f[k]==k)return k;
return f[k]=find(f[k]);
}
int main(){
int tot = 0;
cin >> n >> m;
for(int i = 1; i <= n; i++) f[i] = i;
for(int i = 1, u, v, w; i <= m; i++){
cin >> u >> v >> w;
a[i].u = u, a[i].v = v, a[i].w = w;
}
sort(a+1, a + m + 1, cmp);
for(int i = 1; i <= m; i++){
if(find(a[i].u) == find(a[i].v)) continue;
as += a[i].w;
f[find(a[i].v)] = find(a[i].u);
if(++tot == n-1) break;
}
if(tot != n-1){
cout << "orz";
return 0;
}
cout << as;
}
证明(摘自OI.WIKI)
思路很简单,为了造出一棵最小生成树,我们从最小边权的边开始,按边权从小到大依次加入,如果某次加边产生了环,就扔掉这条边,直到加入了 条边,即形成了一棵树。
证明:使用归纳法,证明任何时候 K 算法选择的边集都被某棵 MST 所包含。
基础:对于算法刚开始时,显然成立(最小生成树存在)。
归纳:假设某时刻成立,当前边集为 \(F\),令 \(T\) 为这棵 MST,考虑下一条加入的边 \(e\)。
如果 \(e\) 属于 \(T\),那么成立。
否则,\(T + e\) 一定存在一个环,考虑这个环上不属于 \(F\) 的另一条边 \(f\)(一定只有一条)。
首先,\(f\) 的权值一定不会比 \(e\) 小,不然 \(f\) 会在 \(e\) 之前被选取。
然后, \(f\) 的权值一定不会比 \(e\) 大,不然 就是一棵比 \(T\) 还优的生成树了。
所以,\(T + e - f\) 包含了 \(F\) ,并且也是一棵最小生成树,归纳成立。
Prim 算法
实现
Prim 算法的基本思想是从一个结点开始,不断加点(而不是 Kruskal 算法的加边)。
具体来说,每次要选择距离最小的一个结点,以及用新的边更新其他结点的距离。
有一个观察:对应于每个点,其出边边权最小的那个边一定在最小生成树里面。
其实跟 Dijkstra 算法一样,每次找到距离最小的一个点,可以暴力找也可以用堆维护。
堆优化的方式类似 Dijkstra 的堆优化,但如果使用二叉堆等不支持 \(O(1)\) decrease-key 的堆,复杂度就不优于 Kruskal,常数也比 Kruskal 大。所以,一般情况下都使用 Kruskal 算法,在稠密图尤其是完全图上,暴力 Prim 的复杂度比 Kruskal 优,但 不一定 实际跑得更快。
代码(未优化版)
#include <bits/stdc++.h>
#define maxn 500005
#define int long long
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int n, m;
struct edge{
int v, w, nxt;
}e[maxn];
int head[maxn], cnt;
void add(int u, int v, int w) {
e[++cnt] = { v, w, head[u] };
head[u] = cnt;
}
int dis[maxn], vis[maxn];
int Prim() {
int now = 1, tot = 0, ans = 0;
memset(dis, 0x3f, sizeof(dis));
dis[1] = 0;
for (int i = head[1]; i; i = e[i].nxt) {
int y = e[i].v, z = e[i].w;
dis[y] = min(dis[y], e[i].w);
}
while (++tot < n) {
int mi = 0x3f3f3f3f;
vis[now] = 1;
for (int i = 1; i <= n; i++)
if (!vis[i] && mi > dis[i]) mi = dis[i], now = i;
ans += mi;
for (int i = head[now]; i; i = e[i].nxt) {
int y = e[i].v;
if (dis[y] > e[i].w && !vis[y]) dis[y] = e[i].w;
}
}
return ans;
}
signed main() {
n = read(), m = read();
for (int i = 1; i <= m; i++) {
int u = read(), v = read(), w = read();
add(u, v, w), add(v, u, w);
}
int ans = Prim();
if (ans > 1e9) cout << "orz";
else cout << ans;
}
最短路
Dijkstra算法
用于非负边权的单源最短路求解。
为什么不能处理负权呢?
因为当把一个节点选入集合 \(S\) 时,即意味着已经找到了从源点到这个点的最短路径,但若存在负权边,就与这个前提矛盾,可能会出现得出的距离加上负权后比已经得到 \(S\) 中的最短路径还短。(无法回溯)
流程
将结点分成两个集合:已确定最短路长度的点集(记为 \(S\) 集合)的和未确定最短路长度的点集(记为 \(T\) 集合)。一开始所有的点都属于 \(T\) 集合。
初始化 ,其他点的\(dis()\)均为 $ +\infty$。
然后重复这些操作:
- 从 集合中,选取一个最短路长度最小的结点,移到 集合中。
- 对那些刚刚被加入 集合的结点的所有出边执行松弛操作。
直到 集合为空,算法结束。
代码实现
1.暴力
不使用任何数据结构进行维护,每次 2 操作执行完毕后,直接在 \(T\) 集合中暴力寻找最短路长度最小的结点。
2.二叉堆优化
每成功松弛一条边 \((u, v)\),就将 插入二叉堆中(如果 \(v\) 已经在二叉堆中,直接修改相应元素的权值即可),1 操作直接取堆顶结点即可。共计 \(m\) 次二叉堆上的插入(修改)操作,\(n\) 次删除堆顶操作。
int dist[maxn], v[maxn];
priority_queue<pair<int, int> > q;
void dijkstra(){
memset(dist, 0x3f, sizeof(dist));
memset(v, 0, sizeof(v));
dist[s] = 0;
q.push(make_pair(0, s));
while(!q.empty()){
int x = q.top().second, d = q.top().first; q.pop();
if(v[x]) continue;
v[x] = 1;
for(int i = head[x]; i; i = e[i].nxt){
int y = e[i].v, z = e[i].w;
if(dist[y] > dist[x] + z){
dist[y] = dist[x] + z;
q.push(make_pair(-dist[y], y));
}
}
}
}
这里借鉴了李煜东的《算法竞赛进阶指南》,通过存负值来保证小根堆性质,也可手写一个结构体
DP 的思想
\(f[l][i]\)表示是否有 \(s\) 到i的,长度为 \(l\) 的路径。
正向转移,枚举边\((i,j,w)\):\(f[l+w][j]|=f[l][i]\)
优化:只找 dp 值为1,且没有更短的状态更新。
最短路数量:\(f[l+w][j] += f[l][i]\), 加一个cnt数组,如果更新了最短路,更新cnt
Dijkstra求k短路(洛谷P4467)
根据 dijkstra 每次选择最优,第k次拓展到终点时其实就是 k 短路。
用 \(A*\) 优化。
#include <bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
#define maxn 2500
int n, m, st, ed, k, f[maxn], cnt[maxn];
bool v[maxn];
priority_queue<pair<int, int> > q;
struct edge{
int v, w, nxt;
}e[maxn], ef[maxn];
int head[maxn], headf[maxn], cnt1, cntf;
void add(int u, int v, int w){
e[++cnt1] = {v, w, head[u]}, head[u] = cnt1;
ef[++cntf] = {u, w, headf[v]}, headf[v] = cntf;
}
struct data{
int now, pas, val;
vector<int> route;
bool operator < (const data &b) const {
if (val != b.val) return val > b.val;
int sz = min(route.size(), b.route.size());
for (int i = 0; i < sz; i++) {
if (route[i] != b.route[i]) return route[i] > b.route[i];
}
return route.size() > b.route.size();
}
};
void dijkstra() {
memset(f, 0x3f, sizeof(f));
memset(v, 0, sizeof(v));
f[ed] = 0;
q.push(make_pair(0, ed));
while (q.size()) {
int x = q.top().second;
q.pop();
if (v[x]) continue;
v[x] = 1;
for (int i = headf[x]; i; i = ef[i].nxt) {
int y = ef[i].v, z = ef[i].w;
if (f[y] > f[x] + z) {
f[y] = f[x] + z;
q.push(make_pair(-f[y], y));
}
}
}
}
void A_star() {
priority_queue<data> q;
data s;
s.now = st; s.pas = 0; s.val = f[st]; s.route.push_back(st);
q.push(s);
vector<int> v;
memset(cnt, 0, sizeof(cnt));
int tot = 0;
while (q.size()) {
data x = q.top();
q.pop();
cnt[x.now] ++;
if(x.now == ed){
tot ++;
if(tot == k){
cout << x.route[0];
for (int i = 1, sz = x.route.size(); i < sz; i++)
cout << '-' << x.route[i];
return;
}
}
for (int i = head[x.now]; i; i = e[i].nxt) {
int y = e[i].v, z = e[i].w;
v = x.route;
bool visit = 0;
for (int j = 0, sz = v.size(); j < sz; j++) {
if (v[j] == y) {
visit = 1;
break;
}
}
if(visit) continue;
data nx = x;
nx.now = y;
nx.pas = x.pas + z;
nx.val = f[y] + nx.pas;
nx.route.push_back(y);
q.push(nx);
}
}
cout << "No" << endl;
}
int main() {
cin >> n >> m >> k >> st >> ed;
// if(m==759){ 特判,这题卡A*,正解是可持久化可并堆
// printf("1-3-10-26-2-30\n");
// return 0;
// }
for (int i = 1; i <= m; i++) {
int u = read(), v = read(), w = read();
add(u, v, w);
}
dijkstra();
A_star();
}
SPFA
\(SPFA\) 是 \(Bellman-Ford\) 算法的优先队列优化,其复杂度在一般情况下为 $ O (km)$ ,其中\(k\)通常是一个很小的常数,但在一些极端情况下其复杂度可退化至 $ O(nm)$,和暴力的BF一样。
所以,它死了。
但是还是挺好用的。
void spfa(){
vis[0] = 1;
q.push(0);
while (!q.empty()) {
int u = q.front(); q.pop(); vis[u] = 0;
if (tot[u] == n - 1) { cout << -1; return 0; }
tot[u]++;
for (int i = head[u]; i; i = e[i].nxt)
if (dis[e[i].v] < dis[u] + e[i].w) {
dis[e[i].v] = dis[u] + e[i].w;
if (!vis[e[i].v]) vis[e[i].v] = 1, q.push(e[i].v);
}
}
}
一个点最多被入队 \(n\) 次
- 本身是个BFS,因此经过的边数少的路径会先进队列
- 出队再入队之后经过的边数必定加一
- 最短路长度不超过n
spfa判负环
负环的定义是:一条边权之和为负数的回路。
#include<bits/stdc++.h>
#define maxn 50005
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
struct edge{
int v, w, nxt;
}e[maxn];
int head[maxn], cnt;
int n, m;
void add(int u, int v, int w){
e[++cnt].v = v, e[cnt].w = w;
e[cnt].nxt = head[u], head[u] = cnt;
}
void pre(){
for(int i = 1; i <= cnt; i++)
e[i].nxt = e[i].v = e[i].w = head[i] = 0;
cnt = 0;
}
int dis[maxn], vis[maxn], in[maxn];
bool spfa(){
queue<int> q;
memset(dis, 0x3f, sizeof(dis));
memset(vis, 0, sizeof(vis));
memset(in, 0, sizeof(in));
dis[1] = 0, vis[1] = 1;
q.push(1);
while(q.size()){
int x = q.front(); q.pop();
vis[x] = 0;
for(int i = head[x]; i; i = e[i].nxt){
int y = e[i].v, z = e[i].w;
if(dis[y] > dis[x] + z){
dis[y] = dis[x] + z;
in[y] = in[x] + 1;
if(in[y] >= n) return 1;
if(!vis[y]){
q.push(y), vis[y] = 1;
}
}
}
}
return 0;
}
int main() {
int T = read();
while(T--){
n = read(), m = read();
pre();
for(int i = 1; i <= m; i++){
int u = read(), v = read(), w = read();
add(u, v, w);
if(w >= 0) add(v, u, w);
}
if(spfa() == 1) cout << "YES" << endl;
else cout << "NO" << endl;
}
}
Floyd
可求多源最短路。
虽然 \(Floyd\) 的复杂度是 \(\Theta(n^3)\) ,但是可以求多源最短路(所以其存在是有意义的)
\(f[k][i][j]\) 表示从 \(i\) 到 \(j\) 只经过 \(1\) ~ \(k\) 的点的最短路。
状态转移:不经过 k:\(f[k−1][i][j]\)
经过 k:\(f[k−1][i][k]+f[k−1][k][j]\)
可以省略第一维,因此 \(f[i][j]=min(f[i][j],f[i][k]+f[k][j])\)
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
f[i][j] = min(f[i][k] + f[k][j], f[i][j]);
Floyd 的一个重要应用是求传递闭包
一张图的传递闭包定义为一个 \(n\times n\) 的矩阵 \(B=(b_{ij})_{n\times n}\),其中
signed main() {
int n = read();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
dis[i][j] = read();
}
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
dis[i][j] |= dis[i][k] & dis[k][j];
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++)
cout << dis[i][j] << " ";
cout << endl;
}
}
分层图思想
例题
[JLOI2011] 飞行路线
题目描述
Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 \(n\) 个城市设有业务,设这些城市分别标记为 \(0\) 到 \(n-1\),一共有 \(m\) 种航线,每种航线连接两个城市,并且航线有一定的价格。
Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 \(k\) 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少?
输入格式
第一行三个整数 \(n,m,k\),分别表示城市数,航线数和免费乘坐次数。
接下来一行两个整数 \(s,t\),分别表示他们出行的起点城市编号和终点城市编号。
接下来 \(m\) 行,每行三个整数 \(a,b,c\),表示存在一种航线,能从城市 \(a\) 到达城市 \(b\),或从城市 \(b\) 到达城市 \(a\),价格为 \(c\)。
输出格式
输出一行一个整数,为最少花费。
提示
对于 \(100\%\) 的数据,\(2 \le n \le 10^4\),\(1 \le m \le 5\times 10^4\),\(0 \le k \le 10\),\(0\le s,t,a,b\le n\),\(a\ne b\),\(0\le c\le 10^3\)。
[^版权声明:本文为CSDN博主「语法糖likedy」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。]:
根据是否进行题目提供的操作以及操作次数的不同,会产生非常多的情况,如果考虑何时使用操作,情况更是多。如果将在图上求解最短路看成是在二维平面上进行的,引入进行操作的次数 \(k\) 做为第三维,那么这个三维空间就理应可以包含所有的情况,便可以在这个三维空间上解决问题。
每进行一次操作\((k+1)\),除了操作的边,其他边没有任何变化,在 \(k=0,1,2,…,\)时图都是一样的,那么就将图复制成 k+1 份,第 i 层图代表进行了 i 次操作后的图。
每相邻两层图之间的联系,应该决定了一次操作是发生在哪条边上(何时进行操作)。根据操作的特点(对边权的修改)可以 i 层点到 i+1 层点的边来表示一次操作。
例如:有带权边$ <u,v> = w$, 可选操作:修改权值为0
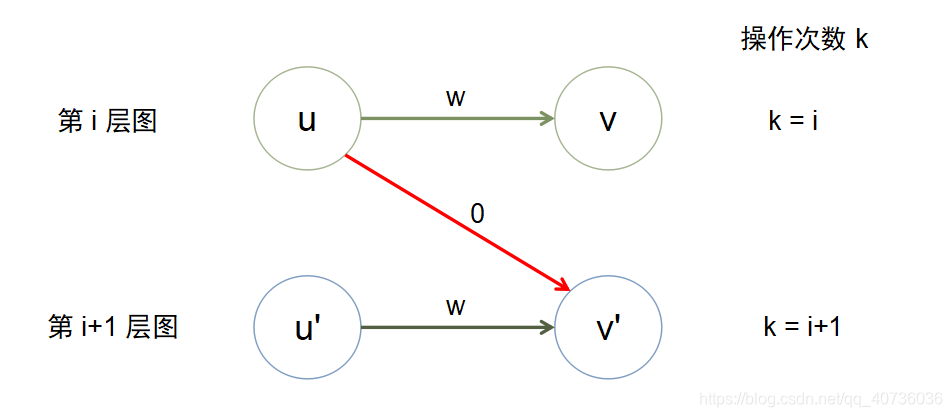
那么对于分层图的构建步骤可以描述为:
1、先将图复制成 \(k+1\) 份 \((0 - k)\)
2、对于图中的每一条边 \(<u,v>\) 从$ u_i$ 到 \(v_{i+1}\) 建立与题目所给操作相对应的边\((i=0,1,…,k)\)
\(k\)代表了进行操作的次数,而每层之间点的关系代表了何时进行操作。
分层图示意图:
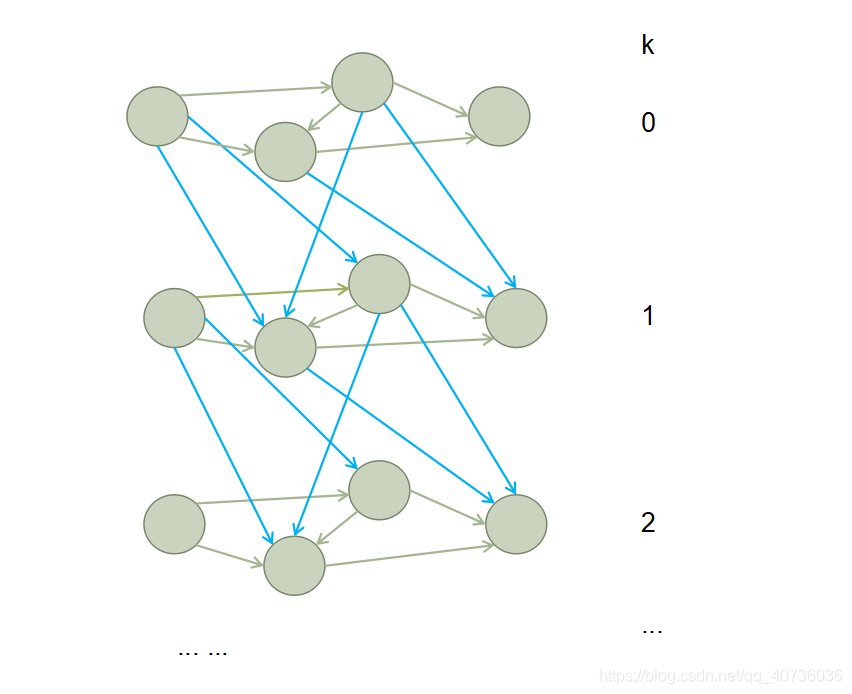
无向图一样处理,因为可以完全看成有向图。
时间复杂度:\(O(k*(m+n)log(n))\)
code:
#include <bits/stdc++.h>
#define maxn 5000005
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int n, m, k, s, t;
struct edge{
int v, w, nxt;
}e[maxn * 2];
int head[maxn], cnt;
void add(int u, int v, int w) {
e[++cnt] = { v, w, head[u] };
head[u] = cnt;
}
int vis[maxn], dis[maxn];
priority_queue < pair<int, int> > q;
void dijkstra() {
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
q.push(make_pair(0, s));
while (!q.empty()) {
int x = q.top().second; q.pop();
if (vis[x]) continue;
vis[x] = 1;
for (int i = head[x]; i; i = e[i].nxt) {
int y = e[i].v;
if (dis[y] > dis[x] + e[i].w) {
dis[y] = dis[x] + e[i].w;
q.push(make_pair(-dis[y], y));
}
}
}
}
signed main() {
n = read(), m = read(), k = read();
s = read(), t = read();
for (int i = 1; i <= m; i++) {
int u = read(), v = read(), w = read();
add(u, v, w), add(v, u, w);
for (int j = 1; j <= k; j++) {
add(u + j * n, v + j * n, w);
add(v + j * n, u + j * n, w);
add(u + (j - 1) * n, v + j * n, 0);
add(v + (j - 1) * n, u + j * n, 0);
}
}
dijkstra();
int ans = 0x3f3f3f3f;
for (int i = 0; i <= k; i++) ans = min(ans, dis[t + i * n]);
cout << ans;
}
最近公共祖先(LCA)
倍增
#include <bits/stdc++.h>
using namespace std;
struct node {
int t, nex;
}e[1000010];
int head[500010], cnt;
void add(int x, int y) {
e[++cnt].t = y;
e[cnt].nex = head[x];
head[x] = cnt;
}
int dep[500001], fa[500001][20], lg[500001];
void dfs(int now, int fath) {
fa[now][0] = fath; dep[now] = dep[fath] + 1;
for(int i = 1; (1 << i) <= dep[now]; i++)
fa[now][i] = fa[fa[now][i-1]][i-1];
for(int i = head[now]; i; i = e[i].nex)
if(e[i].t != fath) dfs(e[i].t, now);
}
int lca(int x, int y) {
if(dep[x] < dep[y]) swap(x, y);
while(dep[x] > dep[y])
x = fa[x][lg[dep[x]-dep[y]] - 1];
if(x == y) return x;
for(int k = lg[dep[x]] - 1; k >= 0; k--)
if(fa[x][k] != fa[y][k])
x = fa[x][k], y = fa[y][k];
return fa[x][0];
}
int main() {
int n, m, s;
cin >> n >> m >> s;
for(int i = 1; i <= n-1; ++i) {
int x, y;
cin >> x >> y;
add(x, y), add(y, x);
}
for(int i = 1; i <= n; ++i)
lg[i] = lg[i-1] + (1 << lg[i-1] == i);
dfs(s, 0);
for(int i = 1; i <= m; ++i) {
int x, y;
cin>> x >> y;
cout << lca(x, y) << endl;
}
return 0;
}
ST表
Tarjan
树剖
图的连通性相关
缩点
模板:P3387 【模板】缩点
这道题如果没有环的话用拓扑排序就可以了,然而这道题是有环的。这些存在从 \(x\) 到 \(y\) 的路径,也存在从 \(y\) 到 \(x\) 的路径,这叫做强连通分量。
对于每个连通分量,我们可以把它缩成一个点,因为如果这个连通分量中有一个点可以经过,那么整个连通分量也可以经过,也就是说,选了这个连通分量中的一个点,其他点也选上才是最优的。
缩完点后就是一张新的图,我们在这张新图上拓扑即可。
下面是缩点和建图代码:
void add(int u, int v){
e[++cnt].v = v, e[cnt].u = u;
e[cnt].nxt = head[u], head[u] = cnt;
}
int dfn[maxn], low[maxn];
int s[maxn];
int n, m;
int tme, top;
int p[maxn], sd[maxn], in[maxn], vis[maxn];
void tarjan(int x){
low[x] = dfn[x] = ++tme;
s[++top] = x, vis[x] = 1;
for(int i = head[x]; i; i = e[i].nxt){
int v = e[i].v;
if(!dfn[v]){
tarjan(v);
low[x] = min(low[x], low[v]);
}
else if(vis[v]) low[x] = min(low[x], dfn[v]);
}
if(dfn[x] == low[x]){
int y = 0;
while(y = s[top--]){
sd[y] = x;
vis[y] = 0;
if(x == y) break;
p[x] += p[y];
}
}
}
int d[maxn];
cin >> n >> m;
for(int i = 1; i <= n; i++) sd[i] = i;
for(int i = 1; i <= n; i++) cin >> p[i];
for(int i = 1; i <= m; i++){
int u ,v ; cin >> u >> v;
add(u, v);
}
for(int i = 1; i <= n; i++) if(!dfn[i]) tarjan(i);
for(int i = 1; i <= m; i++){
int x = sd[e[i].u], y = sd[e[i].v];
if(x != y){
e2[++cnt2].nxt = head2[x];
e2[cnt2].v = y;
e2[cnt2].u = x;
head2[x] = cnt2;
in[y] ++;
}
}
割点
点双连通分量
概念
在一张连通的无向图中,对于两个点 \(u\) 和 \(v\),如果无论删去哪个点(只能删去一个,且不能删 \(u\) 和 \(v\) 自己)都不能使它们不连通,我们就说 \(u\) 和 \(v\) 点双连通。
若一张无向连通图不存在割点,则称它为点双连通图。
对于一张无向图,其极大点双连通子图(就是说不存在比它更大的子图使得这个子图是一个点双连通图)被称为点双连通分量。
无向连通图是“点双连通图”,当且仅当满足下列两个条件之一:
1)图的顶点不超过 \(2\) 个;
2)图中任意两个点都同时包含在一个简单环中。“简单环”指的是不相交的环。
——摘自李煜东《进阶指南》
具体证明可以看《进阶指南》,本蒟蒻不在这里做搬运工了。(逃)
求法
xxxxxxxxxx void dfs(int x){ vis[x] = 1; for(int i = head[x]; i; i = e[i].nxt){ if(vis[e[i].v]) continue; dfs(e[i]) }}cpp
另外,与边双连通分量不同的是,点双连通分量不具有传递性,也就是:如果 \(x\) 与 \(y\) 双连通且 \(y\) 与 \(z\) 双连通, 其实 \(x\) 与\(z\) 不是双连通的。
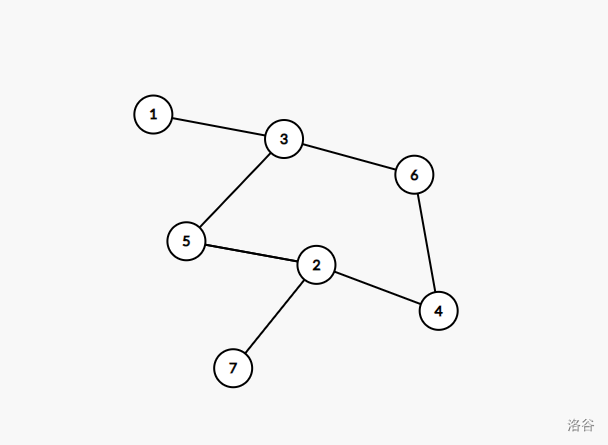
如上图,对于样例四,割点为 \(2\),\(3\), 而这两个割点又分别属于多个点双。
求点双连通分量仍然是用 Tarjan。
Tarjan 算法是什么呢? Tarjan 算法是以美国著名计算机学家 Robert Tarjan 的名字命名的,能够在线性时间内求出无向图的割点与桥(其实还有个与有向图连通性相关的 Tarjan 算法可以求缩点),进而去求出图的双连通分量的算法。
其实 Tarjan 本质就是深搜,同时在深搜时维护时间戳、追溯值等信息和一个栈,通过一些法则来求割点等。
时间戳:时间戳就是在遍历整个无向图时,每个节点第一次被访问的顺序,我们记作 \(dfn(x)\) ;
追溯值: Tarjan 算法引入追溯值 \(low(x)\) ,将 \(low(x)\) 定义为以 \(x\) 为根的子树中 \(dfn(x)\) 与通过一条不在搜索树上的边,到达搜索树中 \(x\) 子树的点的 \(dfn(x)\) 的最小值。
同时,Tarjan 算法还维护一个栈,这个栈是用来维护当前路径上的节点的。先放上这个栈的维护规则,这个从各大网站上一搜就能搜到:
-
在每个节点第一次访问时,就将它入栈;
-
对于 \(x\) 的任意可以到达的节点 \(y\), 当割点判定 \(dfn(x) \leqslant low(y)\) 成立时,无论 \(x\) 是否为根,都要从栈顶不断弹出节点,直到 \(y\) 弹出,并且让弹出的节点与 \(x\) 一起构成一个点双。
至于这个栈是干什么的呢?我们仍然用样例四模拟一下:
当访问到 \(7\),然后回溯时,发现 \(2\) 是个割点。
此时的栈: 1 3 6 4 2 7
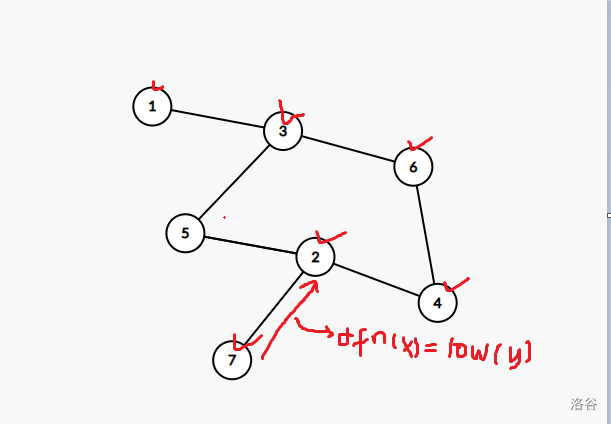
我们将它弹出,让 \(7\) 与 \(2\) 构成一个点双,弹出后: 1 3 6 4 2;
通过 \(5\) 访问到 \(3\) ,回溯时发现符合割点判定定理,此时的栈: 1 3 6 4 2 5
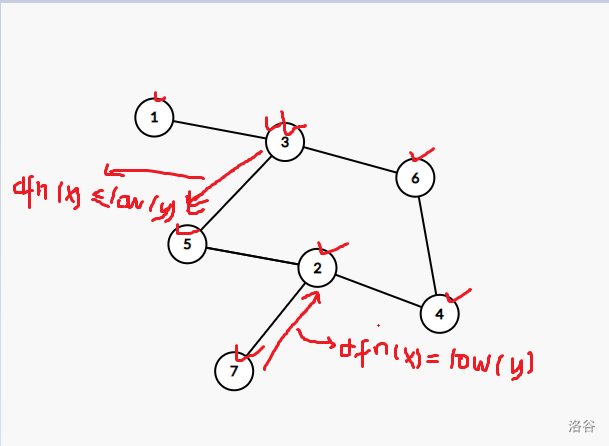
我们把它弹出,弹出元素为: 5 2 4 6 ,让他们与 \(3\) 构成一个点双,剩余的栈: 1 3;
最后同理,在从 \(3\) 回溯到 \(1\) 时也符合割点判定定理,让 \(1\) 与 \(3\) 构成一个点双。
通过模拟,我们可以发现:其实这个栈维护的就是一些有一定连通性的节点,也就是这个栈中所存的节点所构成的图应该没有割点。而当有割点的时候呢?就让这个栈中的节点不断弹出,直到这个栈中没有割点为止,此时,弹出的节点与先前那个割点一同构成一个点双。
为什么能这样呢?我们再返回点双连通分量的定义:对于两个点 \(u\) 和 \(v\),如果无论删去哪个点都不能使它们不连通,这说的不就是要有一定的封闭性吗!
再看割点的定义:在无向连通图中,如果将其中一个点以及所有连接该点的边去掉,图就不再连通,那么这个点就叫做割点。那么我们将无向连通图中的割点去掉,在它形成的几个子图中再分别将割点再加回去,不就是一张无向连通图了吗!
例如还说样例四,将割点去掉后再根据上文所说分别在子图中加入割点的话,就成了这个样子:
这不就是我们所要求的点双连通分量吗!所以说,对于一张无向连通图,将其割点去掉若有 \(n\) 张子图,将每个割点分别在这 \(n\) 子图上加上,就构成了 \(n\) 张没有割点的无向连通图,也就是找到了这 \(n\) 个点双连通分量。 其实上面说的一堆应该就是这个意思(个人见解)。
另:一个孤立点也是一个点双连通分量哦。
代码
最后贴上代码,上面有一些细节。
#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int n, m;
struct edge{
int u, v, nxt;
}e[5 * maxn];
int head[maxn], cnt;
void add(int u, int v){
e[++cnt].v = v, e[cnt].nxt = head[u], head[u] = cnt;
}
int dfn[maxn], low[maxn], tot, s[maxn], top, tme, root;
vector<int> dcc[maxn];
int cut[maxn];
void tarjan(int x){
dfn[x] = low[x] = ++tme;
s[++top] = x;
if(x == root && head[x] == 0){ //这些说明x是一个孤立点,孤立点自身是一个点双
dcc[++tot].push_back(x);
return;
}
for(int i = head[x]; i; i = e[i].nxt){
int y = e[i].v;
if(!dfn[y]){
tarjan(y);
low[x] = min(low[x], low[y]); //更新追溯值
if(low[y] >= dfn[x]){ //符合割点判定定理,弹栈
tot++;
int k;
do{
k = s[top--];
dcc[tot].push_back(k);
}while(k != y);
dcc[tot].push_back(x);
}
}
else low[x] = min(low[x], dfn[y]);
}
}
int main() {
n = read(), m = read();
while(m--){
int u = read(), v = read();
add(u, v), add(v, u);
}
for(int i = 1; i <= n; i++){
root = i;
if(!dfn[i]) tarjan(i);
}
cout << tot << endl;
for(int i = 1; i <= tot; i++){
cout << dcc[i].size() << " ";
for(int j = 0; j < dcc[i].size(); j++){
cout << dcc[i][j] << " ";
}
cout << endl;
}
}
二分图
二分图定义与判定
定义:存在一种点集划分使得同一个集合内的点之间没有边的图是二分图。
二分图的判断:二分图染色
判断一个图是不是二分图:01染色,如果最终没有冲突则是二分图,同一种颜色的属于同一个集合,反之不是。
可以考虑进行二分图的染色,用白色与黑色将每个点染成与其相邻节点不相同的颜色,如果在染色时发现相邻两个点颜色一样,则不构成二分图。当全部染色完后输出 \(\min\) (黑点个数,白点个数) 即可。
int n, m, cntb, cntw, flag;
int nw[maxn], nb[maxn], vis[maxn], in[maxn], col[maxn];
int sum[2];
struct edge {
int v, nxt;
}e[10 * maxn];
int head[maxn], cnt;
void add(int u, int v) {
e[++cnt].v = v;
e[cnt].nxt = head[u], head[u] = cnt;
}
void dfs(int x, int color) {
vis[x] = 1;
col[x] = color;
sum[color] ++;
for (int i = head[x]; i; i = e[i].nxt) {
int y = e[i].v;
if (vis[y]) {
if (col[y] == color) flag = 1;
continue;
}
dfs(y, color ^ 1);
}
}
signed main() {
n = read(), m = read();
for (int i = 1; i <= m; i++) {
int u = read(), v = read();
add(u, v), add(v, u);
in[u] ++, in[v] ++;
}
int ans = 0;
for (int i = 1; i <= n; i++) {
if (!vis[i] && in[i]) {
sum[0] = sum[1] = 0;
dfs(i, 0);
if (flag) {
cout << "Impossible";
return 0;
}
ans += min(sum[0], sum[1]);
}
}
if (flag) cout << "Impossible";
else cout << ans;
}
二分图最大匹配
匈牙利算法(增广路算法)
基本思想
•不断寻找增广路,直至不存在增广路。
•增广路:一条由非匹配边-匹配边-非匹配边-匹配边……交错组成的,由奇数条边组成的路径,当我们找到一条增广路后,可以用非匹配边替代增广路中的匹配边来增加匹配边数。
•dfs寻找增广路,访问过的节点不用重复访问,因此寻找增广路的时间是O(m)的
•在一个匹配中,如果一个非匹配点没有增广路,则存在一个不包含这个点的最大匹配。
其正确性基于 hall 定理,本质是不断寻找增广路来扩大匹配数
匈牙利算法的过程是,枚举每一个左部点 \(u\) ,然后枚举该左部点连出的边,对于一个出点 \(v\),如果它没有被先前的左部点匹配,那么直接将 $ u $ 匹配 \(v\),否则尝试让 \(v\) 的“原配”左部点去匹配其他右部点,如果“原配”匹配到了其他点,那么将 \(u\) 匹配 \(v\),否则 \(u\) 失配。
流程:
extend(x)
遍历每条出边(x,y)
如果目标没有匹配,则找到增广路
否则extend(match[y])
代码实现
int vis[maxn], match[maxn];
bool dfs(int x){
for(int i = head[x]; i; i = e[i].nxt){
int y = e[i].v;
if(!vis[y]){
vis[y] = 1;
if(!match[y] || dfs(match[y])){ //尝试反悔
match[y] = x;
return 1;
}
}
}
return false;
}
//主函数中
for(int i = 1; i <= n; i++){
memset(vis, 0, sizeof(vis));
if(dfs(i)) ++sum;
}
cout << sum << endl;
应用例题
二分图最小点覆盖
定义:对于一张图,其最小点覆盖是一个点数最少的点集使得所有的边都至少有一个端点在点集内。
最小点覆盖 = 最大匹配
最大匹配中任意一条边都需要至少一个端点在集合内,因此最小点覆盖大于等于最大匹配。
利用最大匹配构造最小点覆盖:
- 做一遍增广,记录下所有被访问到的点。
- 左边没被访问的和右边被访问的点组成一个最小点覆盖
二分图最大独立集
定义:对于一张图,其最大独立集是一个点数最多的点集使得点集之间两两没有边。
任何一个点覆盖的补集就是一个独立集,因此最大独立集=n-最小点覆盖。
网络流
基本概念
网络
网络指的是一张有向图 \(G = (V,E)\), 对于 \(u \in V\),\(v \in V\) ,\((u, v) \in E\) 有一权值为 \(c(u, v)\),为这条边的容量,当 \((u, v) \notin E\) ,\(c(u, v) = 0\)。
另有两个特殊点 \(s \in V\) 和 \(t \in V\) ,\((s \ne t)\),分别称作源点、汇点。
流
设 \(f(u, v)\) 是定义在节点二元组 \((u \in V, v \in V)\) 上的实数函数,且满足:
- \(f(u, v) \le c(u, v)\);
- \(f(u, v) = - f(v, u)\);
- \(\forall x \ne s, x \ne t\),\(\sum_{(u, x)}f(u, x) = \sum_{(x, v)}f(x, v)\);
这三条定律分别称为容量限制、斜对称、流量守恒。
我们可以用一个例子来解释:源点就是自来水厂,汇点就是你家,你家和自来水厂用管道连接。这三条定律分别说的是:你给自来水厂交钱之后自来水厂可以给你家疯狂灌水,但是有管道的限制,不可能超出管道容量。第二个说的是,自来水厂给你家灌了 \(x\) 升水,相当于你家往自来水厂灌了 \(-x\) 升水。第三条说的是,管道只是管道,不能存水,流进了多少水,就要流出去多少水。
流函数的完整定义为:
不过这里要注意一下,对于反向的流量是负数这一点可能很难理解,实际上算法导论上并没有给出这斜对称一性质,“反向边”这个概念在残留网络时才会提到,用于退流。建图时可能会存在反向边,这时候其实我们可以直接在反向边上加一个节点,由于流量守恒,所以加了节点的新的网络与之前的网络等价。
流量
流量是对于不同的流函数而言的,对于一个可行流,也就是满足上述三条定律是流函数,其流量定义为所有流出源点的流量减去所有流入源点的流量之差,格式化地,即为:\(\sum_{(s, v) \in V} f(s, v) - \sum_{(v,s) \in V} f(v,s)\) 。而最大流即为流量最大的可行流。
最大流
Edmond-Karp 算法
Ek算法的基本思想就是逐一找增广路。
这个算法很简单,就是 BFS 找增广路,然后对其进行 增广,这个思想被称为 \(FF\)增广,而 \(EK\)算法则是对 \(FF\) 的具体实现。
增广路
你可能会问,怎么找?怎么增广?
- 找?我们就从源点一直 BFS 走来走去,碰到汇点就停,然后增广(每一条路都要增广)。我们在 BFS 的时候就注意一下流量合不合法就可以了。
- 增广?其实就是按照我们找的增广路在重新走一遍。走的时候把这条路的能够成的最大流量减一减,然后给答案加上最小流量就可以了。
反向边
增广的时候要注意建造反向边,原因是这条路不一定是最优的,这样子程序可以进行反悔,也就是退流。假如我们对这条路进行增广了,那么其中的每一条边的反向边的流量就是它的流量。
还有关于一些小细节。如果是常用的链式前向星,那么在加入边的时候就要先加入反向边。那么在用的时候呢,我们直接让边的编号异或1 就可以了 。为什么呢?这就是成对存储,我们在加入正向边后加入反向边,就是靠近的,所以可以使用 。我们还要注意一开始的边的编号要设置为1,因为边要从编号 1开始,这样子才有效果。
EK 算法的时间复杂度为 \(\Theta(nm^2)\)(其中 \(n\) 为点数,\(m\) 为边数),但其实网络流的上界是很宽松的,EK算法 \(1000\) ~ \(10000\)一般都能跑过。
#include <bits/stdc++.h>
#define int long long
#define maxn 10005
#define inf 1e9
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
struct edge{
int v, w, nxt;
}e[maxn];
int head[maxn], cnt;
int n, m, s, t;
void add(int u, int v, int w){
e[++cnt].v = v, e[cnt].w = w;
e[cnt].nxt = head[u], head[u] = cnt;
}
queue<int> q;
int v[maxn];
int maxflow = 0;
int incf[maxn], pre[maxn];
bool bfs(){
memset(v, 0, sizeof(v));
while(q.size()) q.pop();
q.push(s), v[s] = 1;
incf[s] = inf;
while(!q.empty()){
int x = q.front();
q.pop();
for(int i = head[x]; i; i = e[i].nxt){
if(e[i].w){
int y = e[i].v;
if(v[y]) continue;
incf[y] = min(incf[x], e[i].w);
pre[y] = i;
q.push(y);
v[y] = 1;
if(y == t) return 1;
}
}
}
return 0;
}
void update(){
int x = t;
while(x != s){
int i = pre[x];
e[i].w -= incf[t];
e[i ^ 1].w += incf[t];
x = e[i ^ 1].v;
}
maxflow += incf[t];
}
signed main() {
n = read(), m = read(), s = read(), t = read();
cnt = 1;
for(int i = 1; i <= m; i++){
int u = read(), v = read(), w = read();
add(u, v, w), add(v, u, 0);
}
while(bfs()) update();
cout << maxflow;
}
Dinic 算法
#include <bits/stdc++.h>
#define int long long
#define maxn 10005
#define inf 1e9
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
struct edge{
int v, w, nxt;
}e[maxn];
int head[maxn], cnt;
int n, m, s, t;
void add(int u, int v, int w){
e[++cnt].v = v, e[cnt].w = w;
e[cnt].nxt = head[u], head[u] = cnt;
}
queue<int> q;
int d[maxn], now[maxn];
bool bfs(){
memset(d, 0, sizeof(d));
while(q.size()) q.pop();
q.push(s);
d[s] = 1;
now[s] = head[s];
while(!q.empty()){
int x = q.front(); q.pop();
for(int i = head[x]; i; i = e[i].nxt){
if(e[i].w && !d[e[i].v]){
q.push(e[i].v);
now[e[i].v] = head[e[i].v];
d[e[i].v] = d[x] + 1;
if(e[i].v == t) return 1;
}
}
}
return 0;
}
int dinic(int x, int flow){
if(x == t) return flow;
int rest = flow, k, i;
for(int i = now[x]; i && rest; i = e[i].nxt){
now[x] = i;
if(e[i].w && d[e[i].v] == d[x] + 1){
k = dinic(e[i].v, min(rest, e[i].w));
if(!k) d[e[i].v] = 0;
e[i].w -= k;
e[i ^ 1].w += k;
rest -= k;
}
}
return flow - rest;
}
int maxflow = 0;
signed main() {
n = read(), m = read(), s = read(), t = read();
cnt = 1;
for(int i = 1; i <= m; i++){
int u = read(), v = read(), w = read();
add(u, v, w), add(v, u, 0);
}
int flow = 0;
while(bfs()){
while(flow = dinic(s, inf)) maxflow += flow;
}
cout << maxflow;
}
模型
题意魔改板子型
例题:【地震逃生】
题目描述
汶川地震发生时,四川**中学正在上课,一看地震发生,老师们立刻带领 \(x\) 名学生逃跑,整个学校可以抽象地看成一个有向图,图中有 \(n\) 个点,\(m\) 条边。\(1\) 号点为教室,\(n\) 号点为安全地带,每条边都只能容纳一定量的学生,超过楼就要倒塌,由于人数太多,校长决定让同学们分成几批逃生,只有第一批学生全部逃生完毕后,第二批学生才能从 \(1\) 号点出发逃生,现在请你帮校长算算,每批最多能运出多少个学生,\(x\) 名学生分几批才能运完。
输入格式
第一行三个整数 \(n,m,x\);以下 \(m\) 行,每行三个整数 \(a,b,c\)(\(1\leq a,b\leq n\),\(0\leq c\leq x\))描述一条边,分别代表从 \(a\) 点到 \(b\) 点有一条边,且可容纳 \(c\) 名学生。
输出格式
两个整数,分别表示每批最多能运出多少个学生,\(x\) 名学生分几批才能运完。如果无法到达目的地(\(n\) 号点)则输出
Orz Ni Jinan Saint Cow!。对于 \(100 \%\) 的数据,\(0 \le x < 2^{31}\),\(1 \le n \le 200\),\(1 \le m \le 2000\)。
这类题就是魔改板子,可以一眼看出直接建图套板子即可。
#include <bits/stdc++.h>
#define int long long
#define maxn 10005
#define inf 1e9
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
struct edge{
int v, w, nxt;
}e[maxn];
int head[maxn], cnt;
int n, m, s, t;
void add(int u, int v, int w){
e[++cnt].v = v, e[cnt].w = w;
e[cnt].nxt = head[u], head[u] = cnt;
}
queue<int> q;
int d[maxn], now[maxn];
bool bfs(){
memset(d, 0, sizeof(d));
while(q.size()) q.pop();
q.push(s);
d[s] = 1;
now[s] = head[s];
while(!q.empty()){
int x = q.front(); q.pop();
for(int i = head[x]; i; i = e[i].nxt){
if(e[i].w && !d[e[i].v]){
q.push(e[i].v);
now[e[i].v] = head[e[i].v];
d[e[i].v] = d[x] + 1;
if(e[i].v == t) return 1;
}
}
}
return 0;
}
int dinic(int x, int flow){
if(x == t) return flow;
int rest = flow, k, i;
for(int i = now[x]; i && rest; i = e[i].nxt){
now[x] = i;
if(e[i].w && d[e[i].v] == d[x] + 1){
k = dinic(e[i].v, min(rest, e[i].w));
if(!k) d[e[i].v] = 0;
e[i].w -= k;
e[i ^ 1].w += k;
rest -= k;
}
}
return flow - rest;
}
int maxflow = 0;
int x = 0;
signed main() {
n = read(), m = read(), x = read();
cnt = 1;
s = 1, t = n;
for(int i = 1; i <= m; i++){
int u = read(), v = read(), w = read();
add(u, v, w), add(v, u, 0);
}
int flow = 0;
while(bfs()){
while(flow = dinic(s, inf)) maxflow += flow;
}
if(maxflow == 0) {
cout << "Orz Ni Jinan Saint Cow!";
return 0;
}
cout << maxflow << " ";
int tmp = x / maxflow;
if(x % maxflow == 0) cout << tmp;
else cout << tmp + 1;
}
类似题目还有:
[USACO4.2]草地排水Drainage Ditches:【洛谷P2740】
[USACO09JAN]Total Flow S:【洛谷P2936】
最小割
选出边权和最小的边使得源点不能到汇点。
最大流最小割定理:最大流 = 最小割
对于以下三个命题,它们互相等价:
- 流函数 \(f\) 是最大流;
- \(f\) 的残留网络 \(G_f\) 中无增广路;
- 存在一种 \(S\) 和 \(T\) 的划分方式,此时 \(f(s,t)=c(s,t)\)。(实际上此时的\(c\) 就是最小割)
模型
二者取一式问题
最小割模型一般是二者取一。
例题:【善意的投票】
题目描述
幼儿园里有 \(n\) 个小朋友打算通过投票来决定睡不睡午觉。
为了照顾一下自己朋友的想法,他们也可以投和自己本来意愿相反的票。
我们定义一次投票的冲突数为好朋友之间发生冲突的总数加上和所有和自己本来意愿发生冲突的人数。
应该怎样投票,才能使冲突数最小?
输入格式
第一行两个整数 \(n,m\)。其中 \(n\) 代表总人数,\(m\) 代表好朋友的对数。
第二行 \(n\) 个整数,第 \(i\) 个整数代表第 \(i\) 个小朋友的意愿:用 \(0、1\) 表示
接下来 \(m\) 行,每行有两个整数 \(i,j\),表示 \(i,j\) 是一对好朋友,我们保证任何两对 \(i,j\) 不会重复。
输出格式
一行一个整数,即可能的最小冲突数。
这样建图:直接将S连向同意的人,T连向不同意的人,若两人是朋友,则在他们之间连一条双向边(这里有些人不理解:若两个人有冲突,则只需要其中任意一个人改变意见就行了,简单说是让a同意b的意见或者b同意a的意见,所以只需割掉一条边满足一种情况就可以了,但是有两种情况,所以建双向边)。最后就是求最小割了,割掉一条边就是一次冲突。直接套上最大流的模板就ok了。
#include <bits/stdc++.h>
#define int long long
#define maxn 190005
#define inf 1e9
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
struct edge{
int v, w, nxt;
}e[maxn];
int head[maxn], cnt;
int n, m, s, t;
void add(int u, int v, int w){
e[++cnt].v = v, e[cnt].w = w;
e[cnt].nxt = head[u], head[u] = cnt;
}
queue<int> q;
int d[maxn], now[maxn];
bool bfs(){
memset(d, 0, sizeof(d));
while(q.size()) q.pop();
q.push(s);
d[s] = 1;
now[s] = head[s];
while(!q.empty()){
int x = q.front(); q.pop();
for(int i = head[x]; i; i = e[i].nxt){
if(e[i].w && !d[e[i].v]){
q.push(e[i].v);
now[e[i].v] = head[e[i].v];
d[e[i].v] = d[x] + 1;
if(e[i].v == t) return 1;
}
}
}
return 0;
}
int dinic(int x, int flow){
if(x == t) return flow;
int rest = flow, k, i;
for(int i = now[x]; i && rest; i = e[i].nxt){
now[x] = i;
if(e[i].w && d[e[i].v] == d[x] + 1){
k = dinic(e[i].v, min(rest, e[i].w));
if(!k) d[e[i].v] = 0;
e[i].w -= k;
e[i ^ 1].w += k;
rest -= k;
}
}
return flow - rest;
}
int tot = 0;
int maxflow = 0;
signed main() {
n = read(), m = read();
s = 0, t = n + 1;
cnt = 1;
for(int i = 1; i <= n; i++) {
int pos = read();
if(pos) add(s, i, 1), add(i, s, 0);
else add(i, t, 1), add(t, i, 0);
}
for(int i = 1; i <= m; i++) {
int u = read(), v = read();
add(u, v, 1), add(v, u, 0);
add(v, u, 1), add(u, v, 0);
}
int flow = 0;
while(bfs()){
while(flow = dinic(s, inf)) maxflow += flow;
}
cout << maxflow;
}
类似例题:
小M的作物:【洛谷P1361】
费用流
给出一个包含 \(n\) 个点和 \(m\) 条边的有向图(下面称其为网络) \(G=(V,E)\),该网络上所有点分别编号为 \(1 \sim n\),所有边分别编号为 \(1\sim m\),其中该网络的源点为 \(s\),汇点为 \(t\),网络上的每条边 \((u,v)\) 都有一个流量限制 \(w(u,v)\) 和单位流量的费用 \(c(u,v)\)。
你需要给每条边 \((u,v)\) 确定一个流量 \(f(u,v)\),要求:
- \(0 \leq f(u,v) \leq w(u,v)\)(每条边的流量不超过其流量限制);
- \(\forall p \in \{V \setminus \{s,t\}\}\),\(\sum_{(i,p) \in E}f(i,p)=\sum_{(p,i)\in E}f(p,i)\)(除了源点和汇点外,其他各点流入的流量和流出的流量相等);
- \(\sum_{(s,i)\in E}f(s,i)=\sum_{(i,t)\in E}f(i,t)\)(源点流出的流量等于汇点流入的流量)。
定义网络 \(G\) 的流量 \(F(G)=\sum_{(s,i)\in E}f(s,i)\),网络 \(G\) 的费用 \(C(G)=\sum_{(i,j)\in E} f(i,j) \times c(i,j)\)。
SSP算法
SSP(Successive Shortest Path)算法是一个贪心的算法。它的思路是每次寻找单位费用最小的增广路进行增广,直到图上不存在增广路为止。
如果图上存在单位费用为负的圈,SSP 算法正确无法求出该网络的最小费用最大流。此时需要先使用消圈算法消去图上的负圈。
#include <bits/stdc++.h>
#define int long long
#define maxn 10005
#define inf 1e9
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
struct edge{
int v, w, nxt, cost;
}e[10 * maxn];
int head[maxn], cnt;
int n, m, s, t;
void add(int u, int v, int w, int c){
e[++cnt].v = v, e[cnt].w = w;
e[cnt].nxt = head[u], head[u] = cnt;
e[cnt].cost = c;
}
int v[maxn];
int maxflow = 0;
int incf[maxn], pre[maxn], d[maxn];
bool bfs(){
queue<int> q;
memset(v, 0, sizeof(v));
memset(d, 0x3f, sizeof(d));
q.push(s), v[s] = 1, d[s] = 0;
incf[s] = 1 << 30;
while(!q.empty()){
int x = q.front();
v[x] = 0;
q.pop();
for(int i = head[x]; i; i = e[i].nxt){
if(e[i].w){
int y = e[i].v;
if(d[y] > d[x] + e[i].cost){
d[y] = d[x] + e[i].cost;
incf[y] = min(incf[x], e[i].w);
pre[y] = i;
if(!v[y]) v[y] = 1, q.push(y);
}
}
}
}
if(d[t] < 1e9) return 1;
return 0;
}
int ans =0 ;
void update(){
int x = t;
while(x != s){
int i = pre[x];
e[i].w -= incf[t];
e[i ^ 1].w += incf[t];
x = e[i ^ 1].v;
}
maxflow += incf[t];
ans += d[t] * incf[t];
}
signed main() {
n = read(), m = read(), s = read(), t = read();
cnt = 1;
for(int i = 1; i <= m; i++){
int u = read(), v = read(), w = read(), c = read();
add(u, v, w, c), add(v, u, 0, -c);
}
while(bfs()) update();
cout << maxflow << " " << ans;
}
模型
拆点
例题:【餐巾计划问题】
题目描述
一个餐厅在相继的 \(N\) 天里,每天需用的餐巾数不尽相同。假设第 \(i\) 天需要 \(r_i\)块餐巾( i=1,2,...,N)。餐厅可以购买新的餐巾,每块餐巾的费用为 \(p\) 分;或者把旧餐巾送到快洗部,洗一块需 m 天,其费用为 f 分;或者送到慢洗部,洗一块需 \(n\) 天(\(n>m\)),其费用为 \(s\) 分(\(s<f\))。
每天结束时,餐厅必须决定将多少块脏的餐巾送到快洗部,多少块餐巾送到慢洗部,以及多少块保存起来延期送洗。但是每天洗好的餐巾和购买的新餐巾数之和,要满足当天的需求量。
试设计一个算法为餐厅合理地安排好 \(N\) 天中餐巾使用计划,使总的花费最小。编程找出一个最佳餐巾使用计划。
输入格式
由标准输入提供输入数据。文件第 1 行有 1 个正整数 \(N\),代表要安排餐巾使用计划的天数。
接下来的一行是餐厅在相继的 \(N\) 天里,每天需用的餐巾数。
最后一行包含5个正整数\(p,m,f,n,s\)。\(p\) 是每块新餐巾的费用; \(m\) 是快洗部洗一块餐巾需用天数; \(f\) 是快洗部洗一块餐巾需要的费用; \(n\) 是慢洗部洗一块餐巾需用天数; \(s\) 是慢洗部洗一块餐巾需要的费用。
输出格式
将餐厅在相继的 N 天里使用餐巾的最小总花费输出
我们拆点,将一天拆成晚上和早上,每天晚上会受到脏餐巾(来源:当天早上用完的餐巾,在这道题中可理解为从原点获得),每天早上又有干净的餐巾(来源:购买、快洗店、慢洗店)。
1.从原点向每一天晚上连一条流量为当天所用餐巾x,费用为0的边,表示每天晚上从起点获得x条脏餐巾。
2.从每一天早上向汇点连一条流量为当天所用餐巾x,费用为0的边,每天白天,表示向汇点提供x条干净的餐巾,流满时表示第i天的餐巾够用 。 3.从每一天晚上向第二天晚上连一条流量为INF,费用为0的边,表示每天晚上可以将脏餐巾留到第二天晚上(注意不是早上,因为脏餐巾在早上不可以使用)。
4.从每一天晚上向这一天+快洗所用天数t1的那一天早上连一条流量为INF,费用为快洗所用钱数的边,表示每天晚上可以送去快洗部,在地i+t1天早上收到餐巾 。
5.同理,从每一天晚上向这一天+慢洗所用天数t2的那一天早上连一条流量为INF,费用为慢洗所用钱数的边,表示每天晚上可以送去慢洗部,在地i+t2天早上收到餐巾 。
6.从起点向每一天早上连一条流量为INF,费用为购买餐巾所用钱数的边,表示每天早上可以购买餐巾 。 注意,以上6点需要建反向边!3~6点需要做判断(即连向的边必须<=n)
#include <bits/stdc++.h>
using namespace std;
#define maxn 200005
#define int long long
const int inf = 1e14 + 7;
inline int read() {
int x = 0, f = 1; char c = getchar();
while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
int N, p, m, n, f, s1;
int s, t;
struct edge {
int v, w, c, nxt;
}e[maxn];
int head[maxn], cnt;
void add(int u, int v, int w, int c) {
e[++cnt].v = v, e[cnt].w = w;
e[cnt].c = c;
e[cnt].nxt = head[u], head[u] = cnt;
}
int v[maxn];
int maxflow = 0;
int incf[maxn], pre[maxn], d[maxn];
bool bfs() {
queue<int> q;
memset(v, 0, sizeof(v));
memset(d, 0x3f, sizeof(d));
q.push(s), v[s] = 1, d[s] = 0;
incf[s] = 1 << 30;
while (!q.empty()) {
int x = q.front();
v[x] = 0;
q.pop();
for (int i = head[x]; i; i = e[i].nxt) {
if (e[i].w) {
int y = e[i].v;
if (d[y] > d[x] + e[i].c) {
d[y] = d[x] + e[i].c;
incf[y] = min(incf[x], e[i].w);
pre[y] = i;
if (!v[y]) v[y] = 1, q.push(y);
}
}
}
}
if (d[t] < 1e9) return 1;
return 0;
}
int ans = 0;
void update() {
int x = t;
while (x != s) {
int i = pre[x];
e[i].w -= incf[t];
e[i ^ 1].w += incf[t];
x = e[i ^ 1].v;
}
maxflow += incf[t];
ans += d[t] * incf[t];
}
signed main() {
N = read();
s = 0, t = 2 * N + 1;
cnt = 1;
for (int i = 1; i <= N; i++) {
int r = read();
add(s, i, r, 0), add(i, s, 0, 0);
add(i + N, t, r, 0), add(t, i + N, 0, 0);
}
p = read(), m = read(), f = read(), n = read(), s1 = read();
for (int i = 1; i <= N; i++) {
add(s, i + N, inf, p), add(i + N, s, 0, -p);
if (i + 1 <= N)
add(i, i + 1, inf, 0), add(i + 1, i, 0, 0);
if (i + m <= N)
add(i, i + N + m, inf, f), add(i + N + m, i, 0, -f);
if (i + n <= N)
add(i, i + N + n, inf, s1), add(i + N + n, i, 0, -s1);
}
while (bfs()) update();
cout << ans;
}
除了将一天拆为早上和晚上,还可以将一个点拆为进入的点和出去的点,如K取方格数;也可以将一个人拆成多个人,如美食节
动态加边费用流
https://www.luogu.com.cn/problem/P2050
动态规划
动态规划的引入
动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家贝尔曼(R.Bellman)等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。动态规划的应用极其广泛,包括工程技术、经济、工业生产、军事以及自动化控制等领域,并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。
——百度百科
动态规划与分治法相似,都是通过组合子问题来求解原问题。根据算法导论,Programming 译作“表格法”而不是“编写程序”,“动态规划”这个名字网络上有段子说是用来讨要经费的。
包含如下特征:
- 阶段 问题被划分为若干阶段,每阶段受先前阶段影响
- 状态 描述该阶段特定子问题的若干变量
- 决策 从一个状态演变到下一阶段某个状态的选择
- 最优子结构 一个最优化策略的子策略总是最优的
- 无后效性 已经求解的子问题,不会再受到后续决策的影响
OI 中 DP 的含义被极大地扩展了,下面提取两大核心特征
-
状态 一个含义清晰且独立 (即无后效性) 的子问题 $I $
▶ 使用 \(f_I\) 表示子问题 $ I$ 的答案
▶ 可能需要引入辅助子问题 $g_J, h_K, · · · $
-
转移 答案 \(f_I\) 通过状态转移方程由其它子问题共同计算得到
▶ 以状态为点,转移为边,构成有向无环图 (DAG)
▶ 边界条件与平凡子问题
▶ 解空间中的任意元素都被恰当考虑
如何理解最后一句话?按照问题类型分类
- 最优化 (k-优) 最优解能被考虑到,这依赖于最优子结构
- 计数 (概率, 期望) 计数对象 (事件) 能被不重不漏地处理
使用动态规划需要满足以下性质:
1.最优子结构性质。动态规划下一阶段的最优解应该能由前面已经算出的各阶段的最优解导出。
举个简单的例子。下面是一个地图,我们要找一条从左下角(起点)到右上角(终点)、只向右和向上走的路径。

如果要让路径经过的数字总和最大,那么最优路径是下面这条:

可以验证,对于最优路径上的任意一点,最优路径从起点到该点的部分,也正是从起点到该点的所有路径中数字总和最大的那一条。这就叫「满足最优子结构」。
现在换一个「最优」的标准,要求路径经过的数字总和的绝对值最小。那么最优路径是下面这条:
但是,对于最优路径上 -4 这个点,最优路径从起点到该点的部分,却不是从起点到该点的所有路径中,数字总和的绝对值最小的那一条,因为下面这条路径上数字总和的绝对值更小:
这就叫「不满足最优子结构」。
常见的最优化问题,问法一般都是「最大」「最小」,不太会出现「绝对值最小」这种奇葩的最优化标准。而问「最大」「最小」的问题,一般都是满足最优子结构的。 (栗子来自知乎 作者:王赟 Maigo)
2.无后效性。动态规划要求已经求解出的子问题不能受后续阶段的影响,也就是说,动态规划时对于状态空间的遍历应该构成一个有向无环图。
例如CSP-J 2020 方格取数 本题可以向上向下走,如果直接设计 \(f(i, j)\) 的状态表示走到格子 \((i, j)\),那么如下图,状态转移形成环形,会产生后效性。

此时进行动态规划时就要设计一个无后效性的状态,如在原状态 \(f(i, j)\) 的基础上加一维表示方向。
3.子问题重叠。动态规划之所以优于爆搜,就是因为它以空间换时间的形式记录了前面所有状态的最优解。
状态、阶段和决策则是动态规划的三要素。动态规划将相同的计算作用在各阶段的同类子问题,这种计算被称为状态转移方程,其实也就是决策,将当前状态转移到下一状态或更新下一状态,或是根据前面的状态计算当前状态。
一般都是通过数字三角形引入:
Number Triangles
题目描述
观察下面的数字金字塔。
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。
7 3 8 8 1 0 2 7 4 4 4 5 2 6 5在上面的样例中,从 \(7 \to 3 \to 8 \to 7 \to 5\) 的路径产生了最大
输入格式
第一个行一个正整数 \(r\) ,表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
输出格式
单独的一行,包含那个可能得到的最大的和。
样例 #1
样例输入 #1
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5样例输出 #1
30【数据范围】 对于 \(100\%\) 的数据,\(1\le r \le 1000\),所有输入在 \([0,100]\) 范围内。
方法一:递归
int solve(int i, int j) {
return a[i][j] + (i == n ? 0 : max(solve(i + 1, j), solve(i + 1, j + 1)));
}
如果数据范围很小,可以考虑爆搜,所有路径条数为 \(2^{n - 1}\) ,所以时间复杂度为 \(\Theta(2^n)\) ,无法接受。
方法二:递推
时间复杂度 \(\Theta(n^2)\)
#include<bits/stdc++.h>
using namespace std;
int a[1001][1001];
int main() {
int n = 0;
cin >> n;
for (int i = 0; i < n; i++)
for (int j = 0; j <= i; j++)
cin >> f[i][j];
for (int i = n - 2; i >= 0; i--)
for (int j = 0; j <= i; j++)
f[i][j] += max(f[i + 1][j], f[i + 1][j + 1]);
cout << f[0][0];
}
方法三:记忆化搜索
我们画出来方法一的搜索树:
用红色圈起来的地方显然是重复计算了,可以用一个数组来记录搜过的状态,如果再次搜到已搜过的状态,就直接返回记录的值,这样没有了重复搜索,时间复杂度是 \(\Theta(n^2)\).
memset(f, -1, sizeof(f));
int solve(int i, int j) {
if (f[i][j] >= 0) return f[i][j];
return f[i][j] = a[i][j] + (i == n ? 0 :
max(solve(i + 1, j), solve(i + 1, j + 1)));
}
线性DP
背包问题
01背包
#include<bits/stdc++.h>
using namespace std;
int w[101],v[101],dp[1001];
int main(){
int t,m;
cin >> t >> m;
for(int i = 1; i <= m;i ++)
cin >> w[i] >> v[i];
for(int i = 1; i <= m;i++) {
for(int j = t; j >= 0;j--) {
if(j >= w[i])
dp[j] = max(dp[j-w[i]] + v[i], dp[j]);
}
}
cout<<dp[t];
}
多重背包
转化为01背包求解
完全背包
模板:P1616 疯狂的采药
#include<bits/stdc++.h>
using namespace std;
long long w[100001],c[100001];
long long dp[10000005];
int main(){
int v,n;
cin>>v>>n;
for(int i=1;i<=n;i++)
cin>>w[i]>>c[i];
for(int i=1;i<=n;i++)
for(int V=w[i];V<=v;V++)
dp[V]=max(dp[V],dp[V-w[i]]+c[i]);
cout<<dp[v];
}
混合背包
模板:P1833 樱花
朴素解法:对于每个物品,判断它属于哪种背包,然后分别用那种背包进行DP。
#include<bits/stdc++.h>
using namespace std;
int dp[100005];
int v[100005], w[100005], p[100005], n;
int main(){
int te, tt, t1, t2;
char c;
cin >> t1 >> c >> t2; te = t1*60 + t2;
cin >> t1 >> c >> t2; tt = t1*60 + t2;
int t = tt - te;
cin >> n;
for(int i = 1; i <= n; i++) cin >> w[i] >> v[i] >> p[i];
for(int i = 1; i <= n; i++){
if(p[i] == 0)
for(int j = w[i]; j <= t; j++)
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
else{
for(int j = 1; j <= p[i]; j++){
for(int k = t; k >= w[i]; k--){
dp[k] = max(dp[k], dp[k-w[i]] + v[i]);
}
}
}
}
cout << dp[t];
}
得分:\(80pts\) 原因:超时
于是考虑一些高效解法:二进制拆分
做法:把每一个物品根据2的多少次方拆分,因为任何数都可以转化为二进制数;
核心思想:把每一个物品拆成很多个,分别计算价值和所需时间,再转化为01背包求解;
最后一点:完全背包可以把他的空间记为999999,不要太大,一般百万就足够了;
记得这时候数组要开大一点,因为是把一个物品拆成多个物品了
#include<bits/stdc++.h>
using namespace std;
int dp[20005];
int v[20005], w[20005], p[20005], n;
int top;
int vo[100005], co[100005];
void binary_split(){ //二进制拆分
for(int i = 1; i <= n; i++){
int cf = 1;
while(p[i] != 0){
co[++top] = w[i] *cf;
vo[top] = v[i] * cf;
p[i] -= cf;
cf *= 2;
if(p[i] < cf){
co[++top] = w[i] * p[i];
vo[top] = v[i] * p[i];
break;
}
}
}
}
int main(){
int te, tt, t1, t2;
char c;
cin >> t1 >> c >> t2; te = t1*60 + t2;
cin >> t1 >> c >> t2; tt = t1*60 + t2;
int t = tt - te;
cin >> n;
for(int i = 1; i <= n; i++){
cin >> w[i] >> v[i] >> p[i];
if(!p[i]) p[i] = 999999;
}
binary_split();
for(int i = 1; i <= top; i++){
for(int j = t; j >= co[i]; j--){
dp[j] = max(dp[j], dp[j-co[i]] + vo[i]);
}
}
cout << dp[t];
}
区间DP
树形DP
树形 DP,即在树上进行的 DP。由于树固有的递归性质,树形 DP 一般都是递归进行的。
树形 DP 的主要实现形式就是 \(dfs\) 。
基本的状态转移方程
选择节点类:
\(dp[i][0]=dp[j][1]\)
\(dp[i][1]=max/min(dp[j][0],dp[j][1])\)
背包类:
\(dp[v][k]=dp[u][k]+val\)
\(dp[u][k]=max(dp[u][k],dp[v][k−1])\)
树形DP一般没有什么固定做法,一种题目有一种题目的做法。
例题
状态压缩DP
状压 DP 是动态规划的一种,通过将状态压缩为整数来达到优化转移的目的。——oi.wiki
状压,即状态压缩的简称,是一种(在数据范围较小的情况下)将每个物品或者东西选与不选的状态“压”成一个整数的方法
通常我们采用二进制状压法,即对于一个我们“压”成的状态,这个整数在二进制下中的1表示某个物品已选,而0代表某个物品未选,这样我们就可以通过枚举这些“压”成的整数来达到枚举所有的物品选与不选的总情况,通常我们称这些情况叫做子集,对于这个状态整数,通常设为s
(对于二进制状压)通过二进制下的位运算来达到判断某个物品选与不选的情况,再通过这个状态来进行一些其他的扩展,所以状压能简化我们对于问题的求解方式
而状压 \(dp\) 正是用到了这一点,通过一个状态来表示整体情况,对于这个情况进行一些最优化操作,最终达到求得全局最优解的目的
首先二进制状压通常要用到一些位运算:
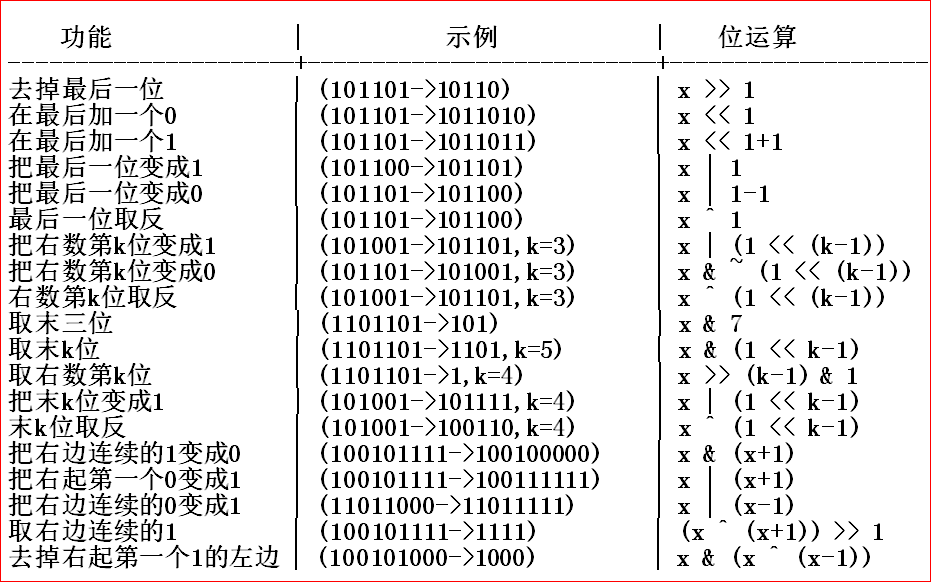
通过一道例题(P3959 [NOIP2017 提高组] 宝藏)来了解状压DP:
首先我们注意到数据范围:\(n <= 12\) ,这提醒我们:可以用状态压缩;
然后整理一下题意,其实就是找一个连边顺序使得所有点连通且代价最小,其中对于一个节点 \(x\) 其可以连通的节点必然对应着两种状态:选或不选,所以可以用状压来做。
设 \(s\) 为已经打通的点所构成的集合,dp[i] [s] [deep] 表示当前 i 节点所对应的选点集合为s,深度为deep
可以写出状态转移方程:$ dp[j] [1<<(j-1) | s] [deep + 1] = dp[i] [s] [deep] + dis[i] * edge_{i , j}$
由于起点不确定,对于每个点都 \(dfs\) 一遍即可。
代码中有详细解释:
#include<bits/stdc++.h>
#define maxn 100005
#define int long long
const int mod = 1e9 + 7;
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int dis[20], dp[15][1<<15][15];
int lim;
int e[20][20]; //用邻接矩阵来存图,可以快速找到从i到j的边权
int as = 1e9; //把答案先初始成一个极大值
int n, m;
void dfs(int s, int sum, int deep){
if(sum >= as) return; //剪枝
if(s == lim){
as = sum; //已经把lim初始化成(1<<n) - 1, 也就是对应所有节点都加入集合的状态
return;
}
for(int i = 1; i <= n; i++){
if(!(1<<(i-1) & s)) continue; //如果i不在s集合中就跳过,因为此时的i不属于这个状态
for(int j = 1; j <= n; j++){
if(!(1<<(j-1) & s) && e[i][j] < 1e9{ //j还没有被探索且i,j之间存在边
if(dp[j][1<<(j-1) | s][deep + 1] <= sum + dis[i] * e[i][j]) continue;
//如果此时的dp所存的最优解要更优就不需要进行状态转移
dp[j][1<<(j-1) | s][deep + 1] = sum + dis[i] * e[i][j];//状态转移方程
dis[j] = dis[i] + 1;//路径增加
dfs(1<<(j-1) | s, dp[j][1<<(j-1) | s][deep + 1], deep + 1);
//在此状态基础上继续搜
}
}
}
}
signed main(){
n = read(), m = read();
lim = (1<<n) - 1;
memset(e, 0x3f, sizeof(e));
for(int i = 1; i <= m; i++){
int u = read(), v = read(), w = read();
e[u][v] = e[v][u] = min(e[u][v], w);//处理重边,因为n只有12而m很大
}
for(int i = 1; i <= n; i++){ //每个点都遍历一次
memset(dis, 0, sizeof(dis));
memset(dp, 0x3f, sizeof(dp));
dis[i] = 1;
dfs(1<<(i-1), 0, 0);
}
cout << as;
}
数位DP
首先来关注一些概念:
数位:把一个数字按照个、十、百、千等等一位一位地拆开,关注它每一位上的数字。如果拆的是十进制数,那么每一位数字都是 0~9,其他进制可类比十进制。
数位 DP:用来解决一类特定问题,这种问题比较好辨认,一般具有这几个特征:
- 要求统计满足一定条件的数的数量(即,最终目的为计数);
- 这些条件经过转化后可以使用「数位」的思想去理解和判断;
- 输入会提供一个数字区间(有时也只提供上界)来作为统计的限制;
- 上界很大(比如 \(10^18\) ),暴力枚举验证会超时。
以上概念均引自oi.wiki
基本原理
考虑人类计数的方式,最朴素的计数就是从小到大开始依次加一。但我们发现对于位数比较多的数,这样的过程中有许多重复的部分。例如,从 7000 数到 7999、从 8000 数到 8999、和从 9000 数到 9999 的过程非常相似,它们都是后三位从 000 变到 999,不一样的地方只有千位这一位,所以我们可以把这些过程归并起来,将这些过程中产生的计数答案也都存在一个通用的数组里。此数组根据题目具体要求设置状态,用递推或 DP 的方式进行状态转移。
数位 DP 中通常会利用常规计数问题技巧,比如把一个区间内的答案拆成两部分相减
基本代码
来看一道模板题:P2602 [ZJOI2010] 数字计数
这道题明显符合 数位DP 的特征,所以用数位的方法做:求出 \([0, a-1]\) 的统计与 \([0, b]\) 的统计然后相减;
首先我们需要一个辅助数组 \(f\) , \(f[i]\) 代表在有i位数字的情况下,每个数字有多少个。如果不考虑前导0,你会发现对于每一个数,它的数量都是相等的,也就是 \(f[i]=f[i-1]*10+10^(i-1)\) ;
怎么知道我们想要的答案呢?
设我们要推得数是 ABCD, 我们先统计最高位: 鉴于我们其实已经求出了09,099,0999……上所有数字个数(f[i],且没有考虑前导0)我们何不把这个A000看成00001000~2000...A000对于不考虑首位每一个式子的数字的出现个数为 A*f[3]。加上首位出现也就是小于A每一个数都出现了 10^3 次,再加上,我们就把A000处理完了。
但是首位处理还不止如此,要注意后面BCD的时候A还会再出现,所以次数加上 BCD+ 1;
然后是处理前导0:前导0情况一定是 0001、0002、0003……0999,0出现次数是 \(10^2\), 所以0再减去 \(10^2\)就行了。
其他位也是一样的,递推即可。
#include<bits/stdc++.h>
#define maxn 100005
#define int long long //注意范围开longlong
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int a, b;
int f[100];
int cnta[100], cntb[100], ten[100];
void solve(int x, int *a){
int num[100] = {0};
int len = 0;
while(x){
num[++len] = x%10; //将数展开
x = x/10;
}
for(int i = len; i >= 1; i--){ //一位一位递推
for(int j = 0; j <= 9; j++)
a[j] += f[i-1] * num[i];
for(int j = 0; j < num[i]; j++)
a[j] += ten[i-1];
int num2 = 0;
for(int j = i-1; j >= 1; j--){
num2 = num2*10 + num[j];
}
a[num[i]] += num2 + 1;
a[0] -= ten[i-1];
}
}
signed main(){
a = read(), b = read();
ten[0] = 1;
for(int i = 1; i <= 15; i++){
f[i] = f[i-1]*10 + ten[i-1]; //预处理
ten[i] = 10*ten[i-1];
}
solve(a-1, cnta), solve(b, cntb);
for(int i = 0; i <= 9; i++) cout << cntb[i] - cnta[i] << " ";
}
DP优化
Bitset 优化
Bitset 维护下标 1, 2, · · · , n 的 01 数组,支持常规的位运算操作 (按位运算, 左移右移, 统计 1 的数量),时间复杂度 \(O(n/w)\),其中 w 为 32 或 64。一般 STL 中自带的 bitset 已经足够快。
常用于布尔值类型的 DP,例如在 \(Floyd\) 算法中使用,即可在 \(O(n^ 3/w)\) 时间内求出传递闭包 (即任意点对间的可达性)
例如:
给定 n 个正整数 \(a_1, a_2, · · · , a_n\),请选择一个和不超过 c 的子集,求 最大可能的和。
考虑 DP,设 \(f_{i,j}\) 表示前 \(i\) 个数字,选出和为 \(j\) 的子集是否可行。使用 \(Bitset\) 加速转移,时间复杂度 \(O(n^2a_i/w)\)。
数据结构优化
一些 DP 的状态转移方程可以通过数据结构的操作完成。
常见的有序列上的线段树 (树状数组),平衡树,分块,树上的点分树,线段树合并等。
线段树优化
最长上升子序列计数
例题
题意
在一行中有\(n\)个格子,从左往右编号为\(1\)到\(n\)。
有\(2\)颗棋子,一开始分别位于位置\(A\)和\(B\)。按顺序给出\(Q\)个要求,每个要求是如下形式:
- 给出一个位置\(x_i\),要求将两个棋子中任意一个移动到位置\(x_i\)。
将一颗棋子移动一格需要花费\(1\)秒,就是说将棋子从\(X\)位置移动到\(Y\)位置需要花费\(|X-Y|\)秒。
为了回答要求,你只能移动棋子,并且同一时刻只能移动一颗棋子。要求的顺序是不可更改的。在同一时间允许两颗棋子在同一个格子内。
最小化答案。
#include <bits/stdc++.h>
#define maxn 400005
using namespace std;
#define int long long
const int inf = 1e15;
inline int read() {
int x = 0, f = 1; char c = getchar();
while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
int n, q, A, B;
int x[maxn];
struct segment_tree {
int ans1, ans2, l, r, tag;
}t[4 * maxn];
void pushup(int p) {
t[p].ans1 = min(t[p << 1].ans1, t[p << 1 | 1].ans1);
t[p].ans2 = min(t[p << 1].ans2, t[p << 1 | 1].ans2);
}
void pushdown(int p) {
t[p << 1].tag += t[p].tag; t[p << 1 | 1].tag += t[p].tag;
t[p << 1].ans1 += t[p].tag; t[p << 1].ans2 += t[p].tag;
t[p << 1 | 1].ans1 += t[p].tag; t[p << 1 | 1].ans2 += t[p].tag;
t[p].tag = 0;
}
void build(int p, int l, int r) {
t[p].l = l, t[p].r = r;
if (l == r) {
if (l == B) t[p].ans1 = l, t[p].ans2 = n - l;
else t[p].ans1 = inf, t[p].ans2 = inf;
return;
}
int mid = (t[p].l + t[p].r) >> 1;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
pushup(p);
}
void modify_seg(int p, int l, int r, int y) {
if (t[p].l >= l && t[p].r <= r) {
t[p].tag += y;
t[p].ans1 += y, t[p].ans2 += y;
return;
}
int mid = (t[p].l + t[p].r) >> 1;
pushdown(p);
if (l <= mid) modify_seg(p << 1, l, r, y);
if (r > mid) modify_seg(p << 1 | 1, l, r, y);
pushup(p);
}
void modify_node(int p, int pt, int y) {
if (t[p].l == pt && t[p].r == pt) {
t[p].ans1 = y + t[p].l;
t[p].ans2 = n - t[p].l + y;
return;
}
pushdown(p);
int mid = (t[p].l + t[p].r) >> 1;
if (pt <= mid) modify_node(p << 1, pt, y);
if (pt > mid) modify_node(p << 1 | 1, pt, y);
pushup(p);
}
int query(int p, int l, int r, int type) {
if (t[p].l >= l && t[p].r <= r) {
if (type == 1) return t[p].ans1;
if (type == 2) return t[p].ans2;
}
int mid = (t[p].l + t[p].r) >> 1;
pushdown(p);
int ans = inf;
if (l <= mid) ans = min(ans, query(p << 1, l, r, type));
if (r > mid) ans = min(ans, query(p << 1 | 1, l, r, type));
pushup(p);
return ans;
}
int query_all(int p) {
if (t[p].l == t[p].r) return t[p].ans1 - t[p].l;
pushdown(p);
return min(query_all(p << 1), query_all(p << 1 | 1));
}
signed main() {
n = read(), q = read(), A = read(), B = read();
build(1, 1, n);
x[0] = A;
for (int i = 1; i <= q; i++) {
x[i] = read();
int lm = query(1, 1, x[i], 2) - n + x[i];
int rm = query(1, x[i], n, 1) - x[i];
modify_seg(1, 1, n, abs(x[i] - x[i - 1]));
modify_node(1, x[i - 1], min(lm, rm));
}
cout << query_all(1);
}
单调队列优化
单调队列一般要维护一些最值,一般要对状态转移方程中 \(\max\) 或 \(\min\) 的内容维护最值,
如:P2627 [USACO11OPEN]Mowing the Lawn G
令 \(dp_{i, 1}\) 表示选第 \(i\) 头牛,\(dp_{i, 0}\) 表示不选。
可以预处理出前缀和:
移出来就是:
因为 \(j\) 时从 \(i - k + 1\) 到 \(i\) 枚举的,所以可以维护一个单调队列维护最值。
数学
一些位运算
常用位运算

a ^ b \(\leq\) a + b
算法常用操作 n&(n-1)
这个操作是算法中常见的,作用是消除数字 n 的二进制表示中的最后一个 1。
看个图就很容易理解了:
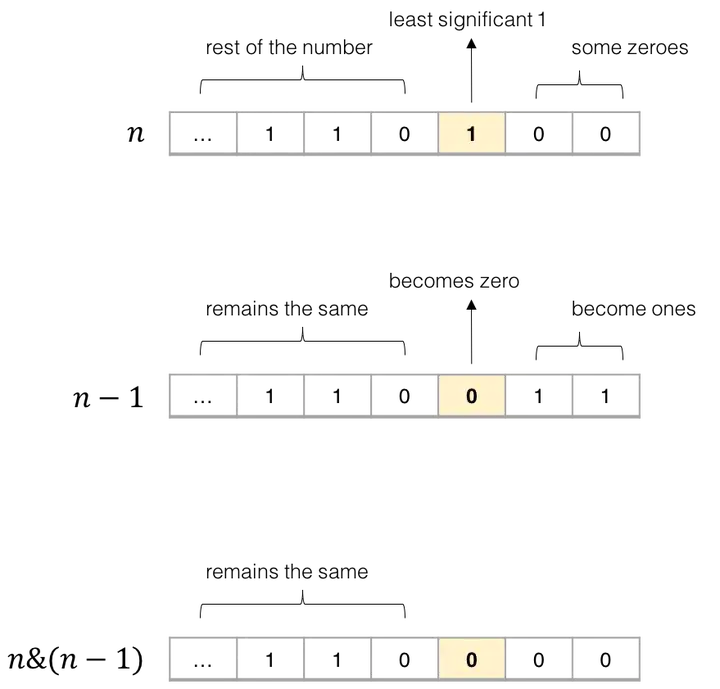
计算汉明权重(Hamming Weight)

就是让你返回 n 的二进制表示中有几个 1。因为 n & (n - 1) 可以消除最后一个 1,所以可以用一个循环不停地消除 1 同时计数,直到 n 变成 0 为止。
int hammingWeight(uint32_t n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
判断一个数是不是 2 的指数
一个数如果是 2 的指数,那么它的二进制表示一定只含有一个 1:
2^0 = 1 = 0b0001
2^1 = 2 = 0b0010
2^2 = 4 = 0b0100
如果使用位运算技巧就很简单了(注意运算符优先级,括号不可以省略):
bool isPowerOfTwo(int n) {
if (n <= 0) return false;
return (n & (n - 1)) == 0;
}
几个有趣的位操作
利用或操作 | 和空格将英文字符转换为小写
('a' | ' ') = 'a'
('A' | ' ') = 'a'
利用与操作 & 和下划线将英文字符转换为大写
('b' & '_') = 'B'
('B' & '_') = 'B'
利用异或操作 ^ 和空格进行英文字符大小写互换
('d' ^ ' ') = 'D'
('D' ^ ' ') = 'd'
以上操作能够产生奇特效果的原因在于 ASCII 编码。字符其实就是数字,恰巧这些字符对应的数字通过位运算就能得到正确的结果
判断两个数是否异号(没啥用)
int x = -1, y = 2;
bool f = ((x ^ y) < 0); // true
int x = 3, y = 2;
bool f = ((x ^ y) < 0); // false
交换两个数
int a = 1, b = 2;
a ^= b;
b ^= a;
a ^= b;
// 现在 a = 2, b = 1
加一
int n = 1;
n = -~n;
// 现在 n = 2
减一
int n = 2;
n = ~-n;
初等数论
最大公约数gcd
因为使用__gcd 等可能会寄……
辗转相除法:
int gcd(int a, int b) {
return (b == 0 ? a : gcd(b, a % b));
}
快速幂
int ksm(int a, int b) { // a^b
int ans = 1;
for (; b; b >>= 1) {
if (b & 1) ans = (long long) ans * a % mod;
a = a * a % mod;
}
return ans;
}
关于取模运算
在模 p 意义下,加减乘法都能保留原有的运算性质
(a mod p + b mod p) mod p = (a + b) mod p
(a mod p − b mod p) mod p = (a − b) mod p
(a mod p) × (b mod p) mod p = (a × b) mod p
类似交换律,结合律,乘法分配律也依然满足 因此,计数题为了方便计算,经常会要求输出答案对某个数取模。
最小公倍数
求解最小公倍数的方法是辗转相除法。
int gcd(int x, int y) {
if(y == 0) return 0;
else return gcd(y, x % y);
}
\(EXGCD\)
对于方程 \(ax + by = \gcd(a, b)\),\(exgcd\) 可以求出一组整数解。
如果 \(b = 0\),则 \(x = 1\),\(y = 0\);
否则递归 \(exgcd(b, a ~mod~ b)\),并求出一组解 \(x ′\) ,$ y ′$ 此时 \(x = y ′\) , \(y = x ′ − ⌊ \frac{a}{b} ⌋y ′\) 是该方程的一组解
int exgcd(int a, int p) {
if (b == 0) {
x = 1, y = 0;
return a;
}
int tmp = x; x = y, y = tmp - (a / b) * y;
return gcd(b, a % b);
}
exgcd 的一个重要应用是求逆元
逆元及求法
当 \(ax≡1(modb)\), x即为 a 在mod b 意义下的逆元。
逆元的数学符号是 inv ,a 在mod b 意义下的逆元记作 inv(a,b)。注意不要写反了。
简单来说逆元就是在mod某个数意义下的倒数。例如5x≡1(mod3)x=2是满足10=1(mod3)所以称2是5在mod3意义下的逆.
逆元有什么用呢?在取模意义下,对于某个数做除法是不行的,正确做法是呈上某个数的逆元再取模。
exgcd 求逆元
\(ax + py = gcd(a, p) = 1\) 那么 \(a*x\) \(mod\) $ p = 1$
\(x\) 为逆元。
int a = read();
int d = exgcd(a, p);
cout << x;
欧拉定理
当 \(\gcd(a, p) = 1\) 时 \(a ^{φ(p)} = 1(modp)\)
$\varphi(nm) = \varphi(n) * \varphi(m),n,m \in \mathbb{P} $
费马小定理
如果 p 是质数且 \(p ∤ a\),则 \(a^{p−1} (modp)\)
也就是 \(a^{p - 2} ~mod~p\) 即为 \(a\) 的逆元。
利用费马小定理求逆元需要用到快速幂。
int power(int a, int b, int p) {
int ans = 1 % p;
for (; b; b >>= 1) {
if (b & 1) ans = (ans * a) % p;
a = (a * a) % p;
}
return ans;
}
signed main() {
n = read(), p = read();
for (int i = 1; i <= n; i++)
cout << power(i, p - 2, p) << endl;
}
线性递推求逆元
首先我们有一个,\(1^{−1}≡1(mod~p)\)
然后设 $ p=k∗i+r,(1<r<i<p) $也就是 \(k\) 是 \(p/i\) 的商,\(r\) 是余数 。
再将这个式子放到(\(mod~p\))意义下就会得到:
\(k∗i+r≡0(mod~p)\)
然后乘上i−1,r−1就可以得到:
\(k∗r−1+i−1≡0(mod~p)\)
\(i−1≡−k∗r−1(mod~p)\)
\(i−1≡−⌊pi⌋∗(p~mod~i)−1(mod~p)\)
于是,我们就可以从前面推出当前的逆元了。
inv[1] = 1;
for (int i = 2; i <= n; i++)
inv[i] = (p - p / i) * inv[p % i] % p;
阶乘的逆元
因为有如下一个递推关系。
\(inv[i+1]=\frac{1}{(i+1)!}\)
\(inv[i+1]∗(i+1)=\frac{1}{i!}=inv[i]\)
所以我们可以求出\(n!\)的逆元,然后逆推,就可以求出\(1...n!\)所有的逆元了。
递推式为
\(inv[i+1]∗(i+1)=inv[i]\)
所以我们可以求出 \(∀i,i!,\frac{1}{i!}\)的取值了。
然后这个也可以导出$ \frac{1}{i }(mod~p) $的取值,也就是
\(\frac{1}{i!}×(i−1)!=\frac{1}{i}(mod~p)\)
草稿(不要看)
除法:mod p 后再除不对(p 是质数)
任何一个 b * a, 不知p, 想要回去就乘上a的乘法逆元(乘上逆元相当于做除法)。
逆元求法
拓展gcd:
对于方程 ax + by = gcd(a, b),exgcd 可以求出一组整数解。 如果 b = 0,则 x = 1,y = 0 否则递归 exgcd(b, a mod b),并求出一组解 x ′ , y ′ 此时 x = y ′ , y = x ′ − ⌊ a/ b ⌋y ′ 是该方程的一组解
求解 \(ax + py = gcd(a, p) = 1\) 那么 \(a*x\) \(mod\) $ p = 1$
x 为逆元
费马小定理
\(a^{p - 2}, a^{p - 1}\) 是 \(a\) 的逆元
矩阵 把A变为I的过程就是把I变成A的逆的过程
线性同余方程
裴蜀定理
内容 \(ax+by=c\) ,\(x \in Z^*, y \in Z*\) ,则其成立的充要条件是 \(\gcd(a, b) | c\)
证明
它的一个重要推论是:a,b互质的充分必要条件是存在整数x,y使ax+by=1.
拓展裴蜀定理 例题
中国剩余定理
中国剩余定理是一种用于求解诸如
\(\begin{cases}x≡a_1\;\;(mod\;\;m_1)\\x≡a_2\;\;(mod\;\;m_2)\\ \cdots \cdots\\x≡a_k\;\;(mod\;\;m_k)\\\end{cases}\)
形式的同余方程组的定理,其中,\(m_1,m_2,...,m_k\) 为两两互质的整数,我们的目的,是找出\(x\)的最小非负整数解。
解法
我们设 M=\(\prod_{i=1}^{k}m_i\qquad\) \(M_i=\frac{M}{m_i}\qquad\) \(M_it_i≡1\;\;(mod\;\;m_i)\)
其中\(1≤i≤k\)。
显然,MM表示所有方程组的模的乘积;\(M_i\) 表示除第ii个方程外,其余所有方程的模的乘积;\(t_i\) 则为\(M_i\)的逆元。
我们可以构造出一个解\(x=\sum_{i=1}^{k}a_iM_it_i\)
由此,任意解\(x_0\)即为 \(x+k*M\)
最小正整数解 \(x_{min}=x_0\,\%\,M\)
Notice: 有人可能会问,\(x=\sum_{i=1}^{k}a_iM_it_i\)中,\(M_it_i\)难道不为1吗?
仔细看,这里x后面跟的是等号,而前面的\(M_it_i≡1\;\;(mod\;\;m_i)≡1\)只有在\(m_i\)的剩余系中才成立,换句话讲,在实数系中,\(M_it_i=1\)是不成立的
线性代数
高斯消元与高斯-约旦消元
概念
高斯消元是一种求解线性方程组的方法。线性方程组是由 \(M\) 个 \(N\) 元一次方程共同构成。线性方程组可以写成 \(M\) 行 \(N\) 列的矩阵,加上等号右边的常数,即可写成一个 \(M\) 行 \(N\) 列的增广矩阵。
如:
求解线性方程组可以进行对增广矩阵的三类操作:
- 用一个非零的数乘某一行
- 将其中一行的若干倍加到另一行上
- 交换两行的位置
这三类操作称为矩阵的“初等行变换”,我们可以用若干次初等行变换求解方程组,如:
最后即可得到矩阵的“上三角矩阵:
再简化一番,可以得到一个”对角矩阵”:
通过初等行变换把增广矩阵简化为上三角矩阵或对角矩阵的过程就是高斯消元。高斯消元的思想是,对于每一个未知量 \(x_i\),找到一个 \(x_i\) 系数非 0,\(x_{1..i-1}\) 系数全为0的方程,通过初等行变换消去其他方程的 \(x_i\) 项。而高斯消元法与高斯-约旦消元法不同的地方在于高斯消元法只消去后面方程组的 \(x_i\) 项,而高斯-约旦消元法将其他所有的 \(x_i\) 项都消去。所以高斯消元法最终得到的是上三角矩阵,而高斯-约旦消元法最终得到的则是对角矩阵。
实现
高斯消元
首先找到一个第一列的数不为0的行(一般找第一列的数最大的行)(如果都为0就跳过当前步)
然后用它的第一列的数将下面行当前列的值化为0,变换过的初等矩阵与原矩阵等价,化为方程后依然成立
本矩阵第一列的数最大的为第三行就把第三行与第一行交换
然后下面行的当前列消去,如图
除了最后一列外,每一列都如此,最后得到上三角矩阵如图

这样我们很容易算出\(x3\)的值,再用\(x3\)的值算出\(x2\),\(x1\)的值
Code
int gauss(int n) {
int r, w = 0;
for (int i = 0; w < n && i < n; i++, w++) { //枚举列(每一项)
r = w;
for (int j = w + 1; j < n; j++)
if (fabs(a[j][i]) > fabs(a[r][i])) //找到最大的系数
r = j;
if (fabs(a[r][i]) < eps) { //是0跳过
w--;
continue;
}
if (w != r) {
for (int j = 0; j <= n; j++) //换到第一行
swap(a[r][j], a[w][j]);
}
for (int k = w + 1; k < n; k++) {
double p = a[k][i] / a[w][i];
for (int j = w; j <= n; j++)
a[k][j] -= p * a[w][j];
}
}
return w; //有效方程数量+1
}
高斯-约旦消元
高斯-约旦消元与高斯消元大体差不多,但消元时上面计算过的行也要消去当前列,最后得到的是对角矩阵而不是上三角矩阵。
Code
int gauss_jordan(int n) {
int r, w = 0;
for (int i = 0; w < n && i < n; i++, w++) {
r = w;
for (int j = w + 1; j < n; j++)
if (fabs(a[j][i]) > fabs(a[r][i]))
r = j;
if (fabs(a[r][i]) < eps) {
w--;
continue;
}
if (w != r) {
for (int j = 0; j <= n; j++)
swap(a[r][j], a[w][j]);
}
for (int k = 0; k < n; k++) { //消去所有方程的xi项
if (k == w) continue;
double p = a[k][i] / a[w][i];
for (int j = n; j >= w; j--)
a[k][j] -= p * a[w][j];
}
}
return w;
}
判断无解与无穷解
注意到我们在函数最后返回了 \(w\),而 \(w-1\) 也就是有效方程个数。(实际上一般增广矩阵从 0 存的话 \(w\) 才是有效方程个数,要从 0 开始记)
如果有效方程个数小于 \(n\),那么就无解了!
然后判断无穷解和无解的情况:
- 如果剩下的方程左边=右边=0,那么就是无穷解答
- 如果剩下方程左边=0,右边!=0,那么就是无解
int d = gauss_jordan(n);
if(d < n){
while(d < n)
if(a[d++][n] != 0) return puts("-1") && 0;
return putchar('0') && 0;
}
博弈论
离散与组合数学
莫比乌斯反演
引入
莫比乌斯反演用处:对于一些函数 \(f(n)\),如果比较难以求出它的值,但容易求出其倍数和或约束和 \(g(n)\),则可以通过莫比乌斯反演简化运算。
莫比乌斯函数
定义
定义 \(\mu\) 为莫比乌斯函数,
详细解释一下后两条,我们令 \(n=\prod_{i=1}^{k}p_i^{c_i}\),也就是将 \(n\) 分解质因数,\(p_i\) 为质因子,\(c_i\ge 1\),则凡是有 \(c_i>1\),\(\mu(n) = 0\),而当任意的 \(c_i\) 都等于 \(1\),\(\mu(n) = (-1) ^ k\)。
性质
证明
既然 \(n=\prod_{i=1}^{k}p_i^{c_i}\) ,那么我们令 \(d = \prod_{i=1}^k p_i^{\beta_i}\),其中 \(0 \le \beta_i \le c_i\)
对于存在 \(\beta_i>=2\) 的情况,\(\mu(d)=0\),我们可以不管。
对于所有 \(\beta_i\) 都小于等于 1 的情况,很显然我们按照\(\beta_i=1\)有几个给它分一下组,也就是按照选了几个质因数给它分组,这样,很显然 \(\mu(d)\) 的值是 \(\C_{k}^0\times(-1)^0 + \C_{k}^1\times(-1)^1+\cdots+\C_{k}^k\times(-1)^k\) 也就是 \(\sum_{i=0}^k\C_k^i\times(-1)^i\)
看到这个形式,我们可以想起来二项式定理:
我们可以令 \(a=1,b=-1\),代入二项式定理正好就是我们刚才推出的式子。
所以
莫比乌斯反演
形式一
定义在正整数域上的两个函数,若
则
莫比乌斯反演相关的题都是去套用这个定理来简化 \(f(n)\) 的计算。
证明
首先将 第一个式子代入第二个式子,消去 \(F(n)\):
这其实就相当于一个二重循环:
for d|n
for i|(n/d)
sum += mu(d) * f(i)
考虑将循环顺序颠倒,没有影响,\(i\) 可遍历到 \(n\) 的任何因数。
再考虑对于 \(\mu(n)\) 的遍历,既然 \(i|\frac nd\),那么 \(di|n\),那么 \(d|\frac ni\)
则:
前面已经证明过 \(\sum_{d|n}\mu(d) = \begin{cases} 1 &n=1\\ 0 & n \ne1 \end{cases}\),则当只有 \(\frac ni = 1\) 时才会对答案有贡献,其他时候都是 0,则 \(i=n\) 时,答案为 \(f(n)\),证毕。
形式二
我们一般会用到莫比乌斯反演的另外一种形式:
证明
形式二的证明与形式一略有不同,但是大致一样。
首先依旧是将第一个式子代入第二个式子。
设 \(d'=\frac dn\),\(d = d'n\),因为 \(d|i\),所以 \(d'n|i\),所以 \(d'|\frac in\)
与前面同理,\(\mu(n)\) 只有在 \(n=1\) 时才是 1,所以最终答案为 \(f(n)\).
例题
VLATTICE - Visible Lattice Points
(太懒了懒得写了回头补

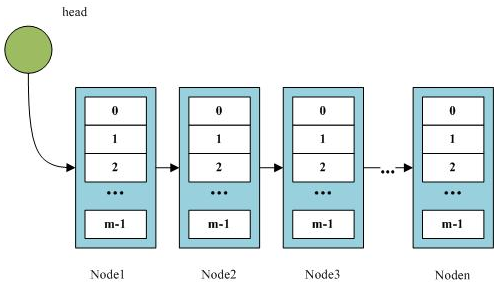

 浙公网安备 33010602011771号
浙公网安备 33010602011771号