最短路
最短路
Dijkstra算法
用于非负边权的单源最短路求解。
为什么不能处理负权呢?
因为当把一个节点选入集合 \(S\) 时,即意味着已经找到了从源点到这个点的最短路径,但若存在负权边,就与这个前提矛盾,可能会出现得出的距离加上负权后比已经得到 \(S\) 中的最短路径还短。(无法回溯)
流程
将结点分成两个集合:已确定最短路长度的点集(记为 \(S\) 集合)的和未确定最短路长度的点集(记为 \(T\) 集合)。一开始所有的点都属于 \(T\) 集合。
初始化 ,其他点的\(dis()\)均为 $ +\infty$。
然后重复这些操作:
- 从 集合中,选取一个最短路长度最小的结点,移到 集合中。
- 对那些刚刚被加入 集合的结点的所有出边执行松弛操作。
直到 集合为空,算法结束。
代码实现
1.暴力
不使用任何数据结构进行维护,每次 2 操作执行完毕后,直接在 \(T\) 集合中暴力寻找最短路长度最小的结点。
2.二叉堆优化
每成功松弛一条边 \((u, v)\),就将 插入二叉堆中(如果 \(v\) 已经在二叉堆中,直接修改相应元素的权值即可),1 操作直接取堆顶结点即可。共计 \(m\) 次二叉堆上的插入(修改)操作,\(n\) 次删除堆顶操作。
int dist[maxn], v[maxn];
priority_queue<pair<int, int> > q;
void dijkstra(){
memset(dist, 0x3f, sizeof(dist));
memset(v, 0, sizeof(v));
dist[s] = 0;
q.push(make_pair(0, s));
while(!q.empty()){
int x = q.top().second, d = q.top().first; q.pop();
if(v[x]) continue;
v[x] = 1;
for(int i = head[x]; i; i = e[i].nxt){
int y = e[i].v, z = e[i].w;
if(dist[y] > dist[x] + z){
dist[y] = dist[x] + z;
q.push(make_pair(-dist[y], y));
}
}
}
}
这里借鉴了李煜东的《算法竞赛进阶指南》,通过存负值来保证小根堆性质,也可手写一个结构体
DP 的思想
\(f[l][i]\)表示是否有 \(s\) 到i的,长度为 \(l\) 的路径。
正向转移,枚举边\((i,j,w)\):\(f[l+w][j]|=f[l][i]\)
优化:只找 dp 值为1,且没有更短的状态更新。
最短路数量:\(f[l+w][j] += f[l][i]\), 加一个cnt数组,如果更新了最短路,更新cnt
Dijkstra求k短路(洛谷P4467)
根据 dijkstra 每次选择最优,第k次拓展到终点时其实就是 k 短路。
用 \(A*\) 优化。
#include <bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
#define maxn 2500
int n, m, st, ed, k, f[maxn], cnt[maxn];
bool v[maxn];
priority_queue<pair<int, int> > q;
struct edge{
int v, w, nxt;
}e[maxn], ef[maxn];
int head[maxn], headf[maxn], cnt1, cntf;
void add(int u, int v, int w){
e[++cnt1] = {v, w, head[u]}, head[u] = cnt1;
ef[++cntf] = {u, w, headf[v]}, headf[v] = cntf;
}
struct data{
int now, pas, val;
vector<int> route;
bool operator < (const data &b) const {
if (val != b.val) return val > b.val;
int sz = min(route.size(), b.route.size());
for (int i = 0; i < sz; i++) {
if (route[i] != b.route[i]) return route[i] > b.route[i];
}
return route.size() > b.route.size();
}
};
void dijkstra() {
memset(f, 0x3f, sizeof(f));
memset(v, 0, sizeof(v));
f[ed] = 0;
q.push(make_pair(0, ed));
while (q.size()) {
int x = q.top().second;
q.pop();
if (v[x]) continue;
v[x] = 1;
for (int i = headf[x]; i; i = ef[i].nxt) {
int y = ef[i].v, z = ef[i].w;
if (f[y] > f[x] + z) {
f[y] = f[x] + z;
q.push(make_pair(-f[y], y));
}
}
}
}
void A_star() {
priority_queue<data> q;
data s;
s.now = st; s.pas = 0; s.val = f[st]; s.route.push_back(st);
q.push(s);
vector<int> v;
memset(cnt, 0, sizeof(cnt));
int tot = 0;
while (q.size()) {
data x = q.top();
q.pop();
cnt[x.now] ++;
if(x.now == ed){
tot ++;
if(tot == k){
cout << x.route[0];
for (int i = 1, sz = x.route.size(); i < sz; i++)
cout << '-' << x.route[i];
return;
}
}
for (int i = head[x.now]; i; i = e[i].nxt) {
int y = e[i].v, z = e[i].w;
v = x.route;
bool visit = 0;
for (int j = 0, sz = v.size(); j < sz; j++) {
if (v[j] == y) {
visit = 1;
break;
}
}
if(visit) continue;
data nx = x;
nx.now = y;
nx.pas = x.pas + z;
nx.val = f[y] + nx.pas;
nx.route.push_back(y);
q.push(nx);
}
}
cout << "No" << endl;
}
int main() {
cin >> n >> m >> k >> st >> ed;
// if(m==759){ 特判,这题卡A*,正解是可持久化可并堆
// printf("1-3-10-26-2-30\n");
// return 0;
// }
for (int i = 1; i <= m; i++) {
int u = read(), v = read(), w = read();
add(u, v, w);
}
dijkstra();
A_star();
}
SPFA
\(SPFA\) 是 \(Bellman-Ford\) 算法的优先队列优化,其复杂度在一般情况下为 $ O (km)$ ,其中\(k\)通常是一个很小的常数,但在一些极端情况下其复杂度可退化至 $ O(nm)$,和暴力的BF一样。
所以,它死了。
但是还是挺好用的。
void spfa(){
vis[0] = 1;
q.push(0);
while (!q.empty()) {
int u = q.front(); q.pop(); vis[u] = 0;
if (tot[u] == n - 1) { cout << -1; return 0; }
tot[u]++;
for (int i = head[u]; i; i = e[i].nxt)
if (dis[e[i].v] < dis[u] + e[i].w) {
dis[e[i].v] = dis[u] + e[i].w;
if (!vis[e[i].v]) vis[e[i].v] = 1, q.push(e[i].v);
}
}
}
一个点最多被入队 \(n\) 次
- 本身是个BFS,因此经过的边数少的路径会先进队列
- 出队再入队之后经过的边数必定加一
- 最短路长度不超过n
spfa判负环
负环的定义是:一条边权之和为负数的回路。
#include<bits/stdc++.h>
#define maxn 50005
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
struct edge{
int v, w, nxt;
}e[maxn];
int head[maxn], cnt;
int n, m;
void add(int u, int v, int w){
e[++cnt].v = v, e[cnt].w = w;
e[cnt].nxt = head[u], head[u] = cnt;
}
void pre(){
for(int i = 1; i <= cnt; i++)
e[i].nxt = e[i].v = e[i].w = head[i] = 0;
cnt = 0;
}
int dis[maxn], vis[maxn], in[maxn];
bool spfa(){
queue<int> q;
memset(dis, 0x3f, sizeof(dis));
memset(vis, 0, sizeof(vis));
memset(in, 0, sizeof(in));
dis[1] = 0, vis[1] = 1;
q.push(1);
while(q.size()){
int x = q.front(); q.pop();
vis[x] = 0;
for(int i = head[x]; i; i = e[i].nxt){
int y = e[i].v, z = e[i].w;
if(dis[y] > dis[x] + z){
dis[y] = dis[x] + z;
in[y] = in[x] + 1;
if(in[y] >= n) return 1;
if(!vis[y]){
q.push(y), vis[y] = 1;
}
}
}
}
return 0;
}
int main() {
int T = read();
while(T--){
n = read(), m = read();
pre();
for(int i = 1; i <= m; i++){
int u = read(), v = read(), w = read();
add(u, v, w);
if(w >= 0) add(v, u, w);
}
if(spfa() == 1) cout << "YES" << endl;
else cout << "NO" << endl;
}
}
Floyd
可求多源最短路。
虽然 \(Floyd\) 的复杂度是 \(\Theta(n^3)\) ,但是可以求多源最短路(所以其存在是有意义的)
\(f[k][i][j]\) 表示从 \(i\) 到 \(j\) 只经过 \(1\) ~ \(k\) 的点的最短路。
状态转移:不经过 k:\(f[k−1][i][j]\)
经过 k:\(f[k−1][i][k]+f[k−1][k][j]\)
可以省略第一维,因此 \(f[i][j]=min(f[i][j],f[i][k]+f[k][j])\)
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
f[i][j] = min(f[i][k] + f[k][j], f[i][j]);
Floyd 的一个重要应用是求传递闭包
一张图的传递闭包定义为一个 \(n\times n\) 的矩阵 \(B=(b_{ij})_{n\times n}\),其中
signed main() {
int n = read();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
dis[i][j] = read();
}
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
dis[i][j] |= dis[i][k] & dis[k][j];
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++)
cout << dis[i][j] << " ";
cout << endl;
}
}
分层图思想
例题
[JLOI2011] 飞行路线
题目描述
Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 \(n\) 个城市设有业务,设这些城市分别标记为 \(0\) 到 \(n-1\),一共有 \(m\) 种航线,每种航线连接两个城市,并且航线有一定的价格。
Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 \(k\) 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少?
输入格式
第一行三个整数 \(n,m,k\),分别表示城市数,航线数和免费乘坐次数。
接下来一行两个整数 \(s,t\),分别表示他们出行的起点城市编号和终点城市编号。
接下来 \(m\) 行,每行三个整数 \(a,b,c\),表示存在一种航线,能从城市 \(a\) 到达城市 \(b\),或从城市 \(b\) 到达城市 \(a\),价格为 \(c\)。
输出格式
输出一行一个整数,为最少花费。
提示
对于 \(100\%\) 的数据,\(2 \le n \le 10^4\),\(1 \le m \le 5\times 10^4\),\(0 \le k \le 10\),\(0\le s,t,a,b\le n\),\(a\ne b\),\(0\le c\le 10^3\)。
[^版权声明:本文为CSDN博主「语法糖likedy」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。]:
根据是否进行题目提供的操作以及操作次数的不同,会产生非常多的情况,如果考虑何时使用操作,情况更是多。如果将在图上求解最短路看成是在二维平面上进行的,引入进行操作的次数 \(k\) 做为第三维,那么这个三维空间就理应可以包含所有的情况,便可以在这个三维空间上解决问题。
每进行一次操作\((k+1)\),除了操作的边,其他边没有任何变化,在 \(k=0,1,2,…,\)时图都是一样的,那么就将图复制成 k+1 份,第 i 层图代表进行了 i 次操作后的图。
每相邻两层图之间的联系,应该决定了一次操作是发生在哪条边上(何时进行操作)。根据操作的特点(对边权的修改)可以 i 层点到 i+1 层点的边来表示一次操作。
例如:有带权边$ <u,v> = w$, 可选操作:修改权值为0
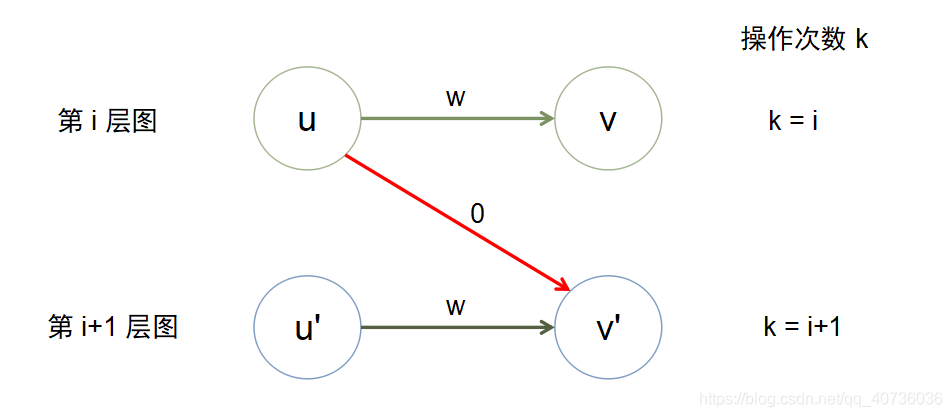
那么对于分层图的构建步骤可以描述为:
1、先将图复制成 \(k+1\) 份 \((0 - k)\)
2、对于图中的每一条边 \(<u,v>\) 从$ u_i$ 到 \(v_{i+1}\) 建立与题目所给操作相对应的边\((i=0,1,…,k)\)
\(k\)代表了进行操作的次数,而每层之间点的关系代表了何时进行操作。
分层图示意图:
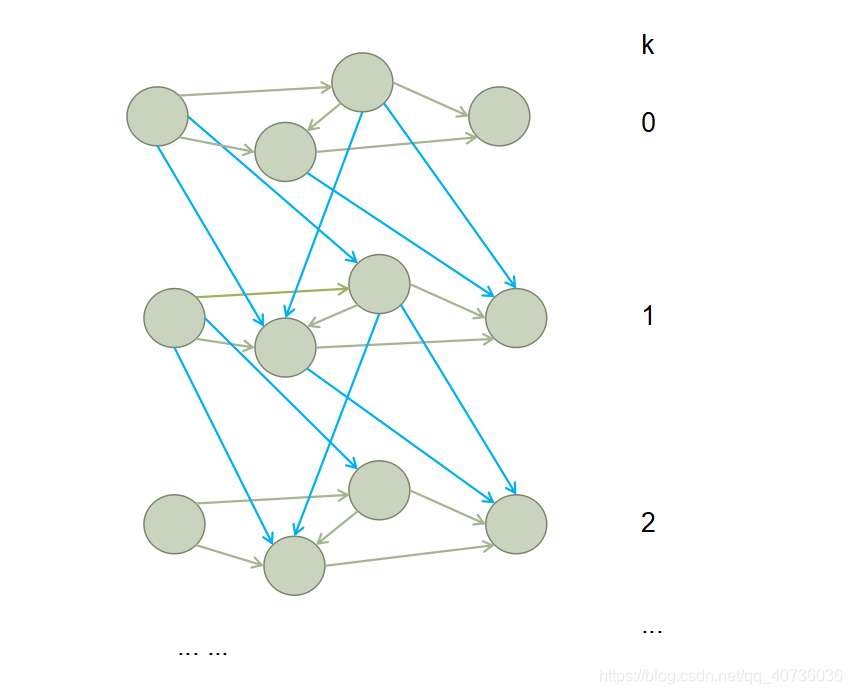
无向图一样处理,因为可以完全看成有向图。
时间复杂度:\(O(k*(m+n)log(n))\)
code:
#include <bits/stdc++.h>
#define maxn 5000005
using namespace std;
inline int read(){
int x = 0 , f = 1 ; char c = getchar() ;
while( c < '0' || c > '9' ) { if( c == '-' ) f = -1 ; c = getchar() ; }
while( c >= '0' && c <= '9' ) { x = x * 10 + c - '0' ; c = getchar() ; }
return x * f ;
}
int n, m, k, s, t;
struct edge{
int v, w, nxt;
}e[maxn * 2];
int head[maxn], cnt;
void add(int u, int v, int w) {
e[++cnt] = { v, w, head[u] };
head[u] = cnt;
}
int vis[maxn], dis[maxn];
priority_queue < pair<int, int> > q;
void dijkstra() {
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
q.push(make_pair(0, s));
while (!q.empty()) {
int x = q.top().second; q.pop();
if (vis[x]) continue;
vis[x] = 1;
for (int i = head[x]; i; i = e[i].nxt) {
int y = e[i].v;
if (dis[y] > dis[x] + e[i].w) {
dis[y] = dis[x] + e[i].w;
q.push(make_pair(-dis[y], y));
}
}
}
}
signed main() {
n = read(), m = read(), k = read();
s = read(), t = read();
for (int i = 1; i <= m; i++) {
int u = read(), v = read(), w = read();
add(u, v, w), add(v, u, w);
for (int j = 1; j <= k; j++) {
add(u + j * n, v + j * n, w);
add(v + j * n, u + j * n, w);
add(u + (j - 1) * n, v + j * n, 0);
add(v + (j - 1) * n, u + j * n, 0);
}
}
dijkstra();
int ans = 0x3f3f3f3f;
for (int i = 0; i <= k; i++) ans = min(ans, dis[t + i * n]);
cout << ans;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号