[学习笔记]回文算法

Manacher

Manacher用以解决一类对每个中心求解其左右两端最长的回文串。

考虑我们先把所有两个字符之间都插入一个不在字符集里的字符，这样就可以不用考虑中心在字符中间的情况，即可以直接枚举中心。

考虑如何使用已知的信息操作。

若我们求\(i\)位置的最长回文半径，设前面极长回文串的最右端为中心为第\(j\)个位置，考虑对称过去为\(p\),则不难发现\(\min(f_p,j + f_j - i)\)一定不大于\(f_i\),我们就可以知道在我们已经扫过的范围内，以\(i\)位置为回文中心的回文串的最长回文半径，接着可以之间暴力枚举。

其复杂度为\(O(n)\)。

点击查看代码

	s[0] = '~';
	a = getchar();
	while(a <= 'z' && a >= 'a'){
		s[++len] = '|';
		s[++len] = a;
		a = getchar();
	}
	s[++len] = '|';
	for(int i = 1;i <= len;++i){
		if(m + ans[m] >= i)
		ans[i] = std::min(m + ans[m] - i,ans[m * 2 - i]);
		while(s[i - ans[i]] == s[i + ans[i]]) ans[i] ++ ;
		if(ans[i] + i > m + ans[m])m = i;
		if(fans < ans[i])
		fans = ans[i];
	} 
	std::cout<<fans - 1;

回文自动机

和其他自动机类似的，回文树也由转移边和后缀连接组成，每个节点都可以代表一个回文子串。

考虑回文串分为奇偶串。

一个节点的\(fail\)表示其最长回文后缀所对应的节点，其转移边不同于其他自动机的在末尾加字符而是同时在开头于结尾加字符以满足回文性质。

顺带在每个节点维护此节点对应的回文子串的长度。

建造

回文树有两个初始阶段，分别表示长度为\(-1,0\)的回文串，称其为奇根，偶根。

偶根的\(fail\)指针指向奇根，我们并不关心奇根的失配指针，因为奇根不会失配，他总是能够转移到一个单字符串。

类似后缀自动机，增量构造回文树。

考虑构造\(p - 1\)的字符串回文树后，向自动机中添加原串里位置为\(p\)的字符。

我们从以上一个字符结尾的最长回文串对应的节点开始，不断沿着\(fail\)指针走，直到找到一个节点满足\(s_p = s_{p - len - 1}\),即下面图中的\(A\)。

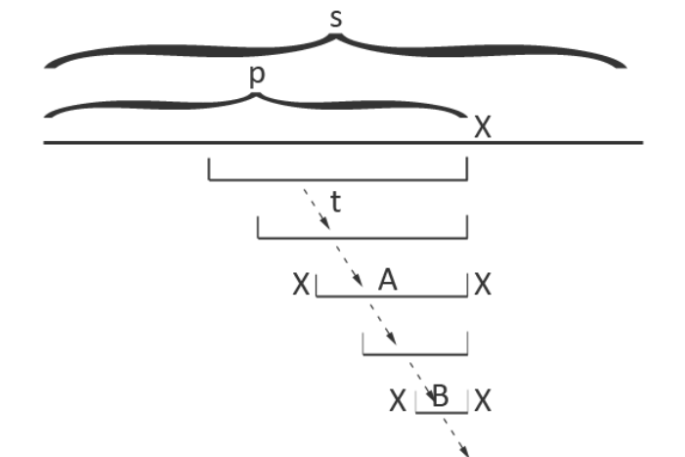
然后根据这个点是否存在新建节点。

然后要求出这个点的\(fail\)，之间跳转\(fail\)指针即可。

如果\(fail\)没匹配到，那么把他连向长度为\(0\)的那个节点。

根据\(oi-wiki\)的证明，其总时空复杂度均为\(O(|S|)\)。

点击查看代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std; 

const int N = 2e6 + 5; 
struct PAM_Trie
{
	int ch[26]; 
	int fail, len, num; 
}; 
struct PAM
{
	PAM_Trie b[N]; 
	int n, length, last, cnt, s[N]; 
	char c[N]; 
	
	PAM()
	{
		b[0].len = 0; b[1].len = -1; 
		b[0].fail = 1; b[1].fail = 0; 
		last = 0; 
		cnt = 1; 
	}
	void read()
	{
		scanf("%s", c + 1); 
		length = strlen(c + 1); 
	}
	int get_fail(int x)
	{
		while(s[n - b[x].len - 1] != s[n])
		{
			//printf("%d %d %d\n", x, n - b[x].len - 1, b[x].fail); 
			x = b[x].fail; 
		}
		return x; 
	}
	void insert()
	{
		int p = get_fail(last); 
		if(!b[p].ch[s[n]])
		{
			b[++cnt].len = b[p].len + 2; 
			int tmp = get_fail(b[p].fail); 
			b[cnt].fail = b[tmp].ch[s[n]]; 
			b[cnt].num = b[b[cnt].fail].num + 1; 
			b[p].ch[s[n]] = cnt; 
		}
		last = b[p].ch[s[n]]; 
	}
	void solve()
	{
		int k = 0; 
		s[0] = 26; 
		for(n = 1; n <= length; n++)
		{
			c[n] = (c[n] - 97 + k) % 26 + 97; 
			s[n] = c[n] - 'a'; 
			insert(); 
			printf("%d ", b[last].num); 
			k = b[last].num; 
		}
	}
}P; 
int main()
{
	P.read(); 
	P.solve(); 
	return 0; 
}