Python: tree 树 Heap Sort

 

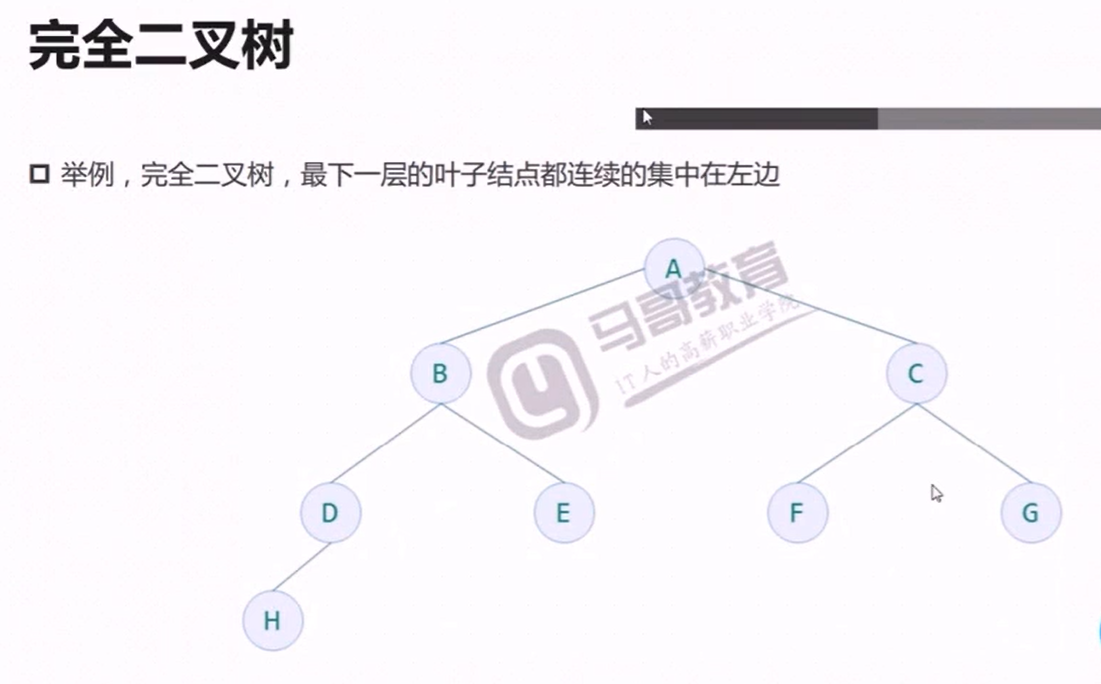
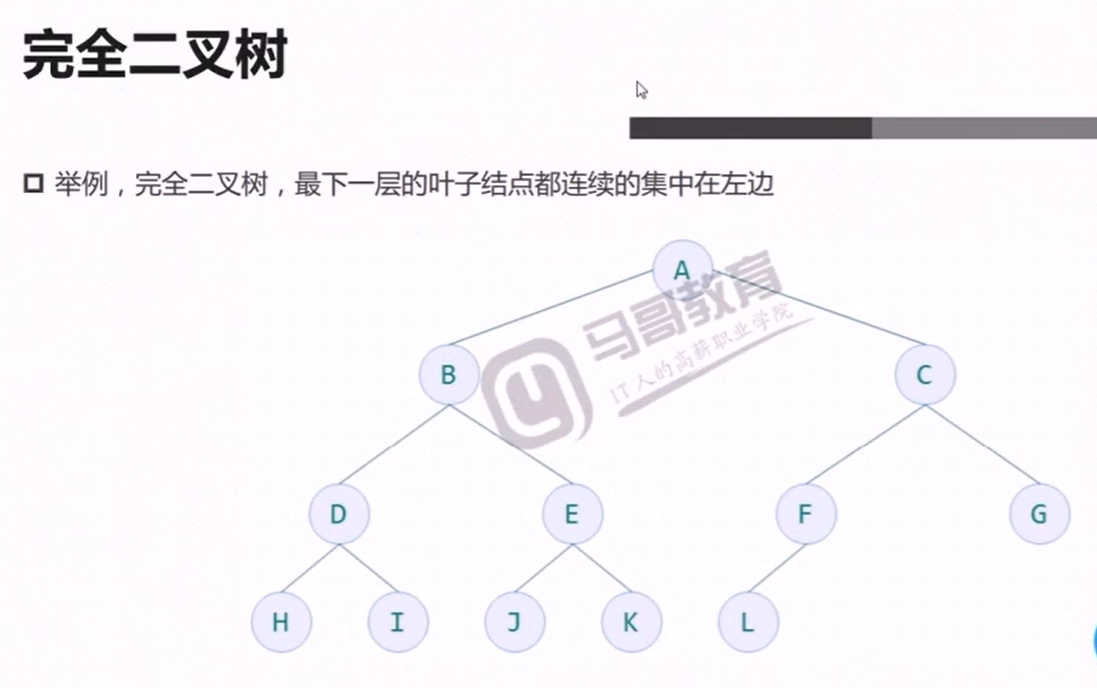
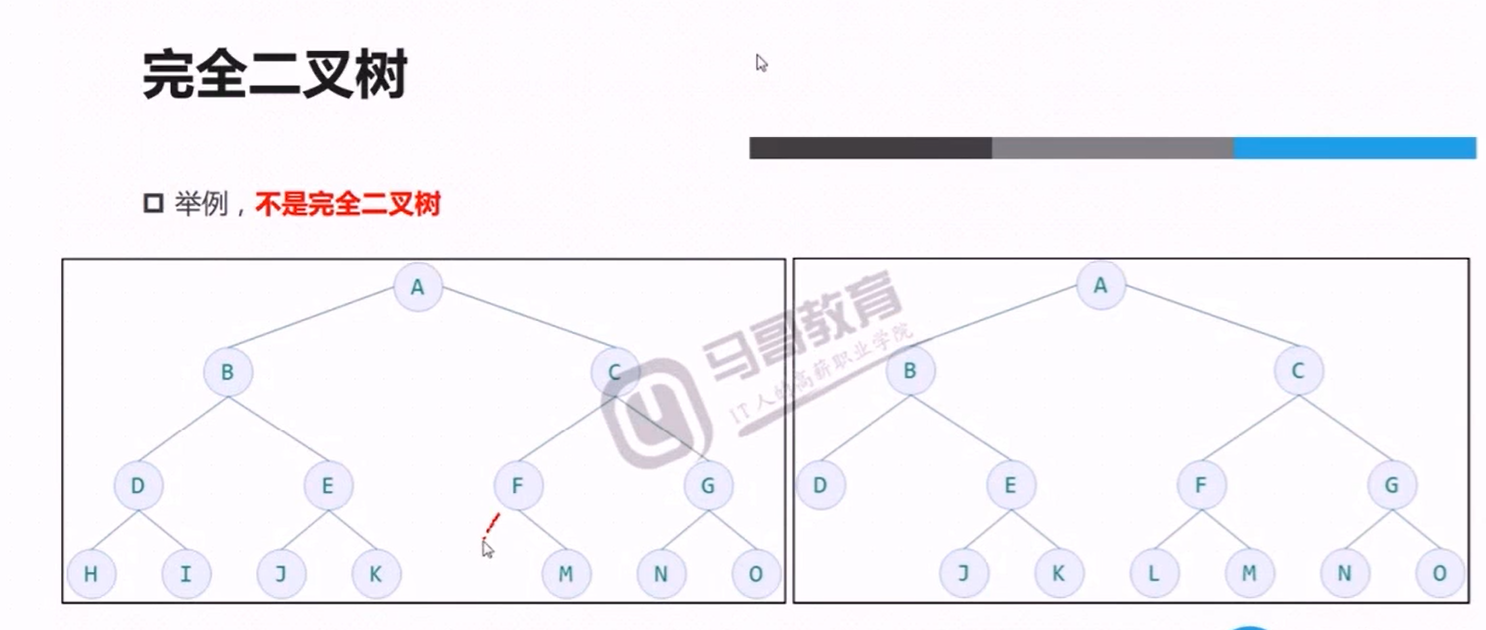
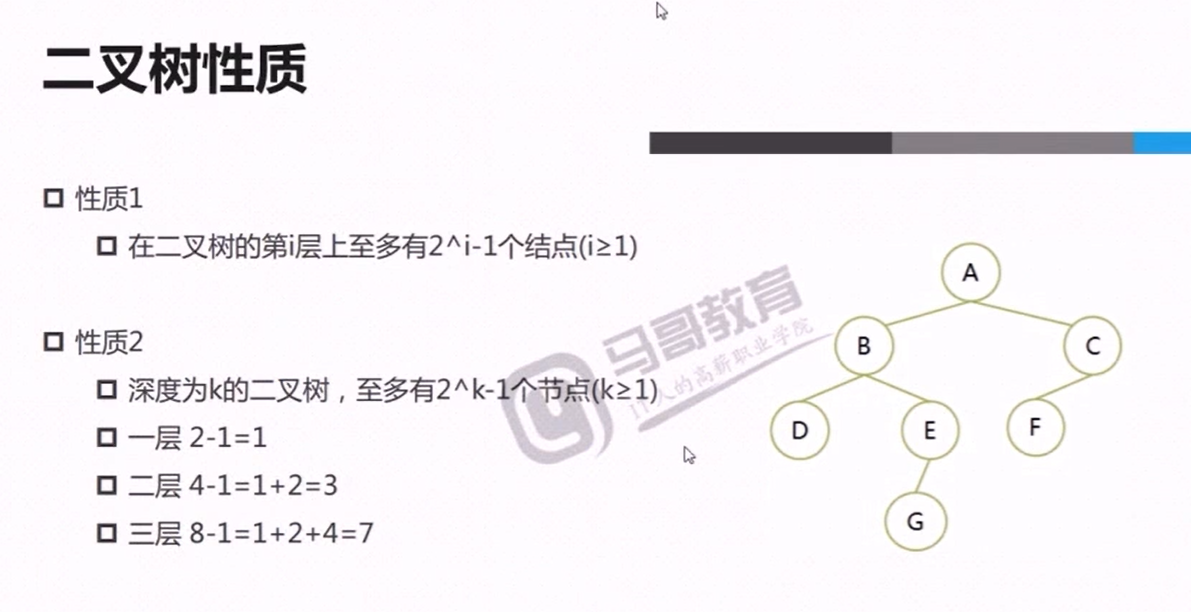
打印Full binary tree:

import math

def reveal(vail: list | tuple):
    """
    利用Python居中打印
    :param vail:
    :return:
    """
    length = len(vail)
    height = math.ceil(math.log2(length + 1))
    width = 2 ** height - 1
    width = 2 * width

    print(f'height: {height}')
    print(f'width: {width}')
    print()

    index = 0

    for b in range(1, height + 1):
        nodes = 2 ** (b - 1)
        for p in range(nodes):
            if index >= length:  # 其实放前放后无所谓(假设计算height=4, 则第四次至少有一个node)
                break
            node = f'{vail[index]:0>2}'
            if p == nodes - 1:
                print(f'{node:^{width}}', end='')
            else:
                print(f'{node:^{width}}', end=' ' * 2)
            index += 1
        # print(' ' * 10, width)
        width = (width - 2) // 2  # 每次减node宽度即可完美整除2
        print()


reveal(list(range(1, 20)))

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

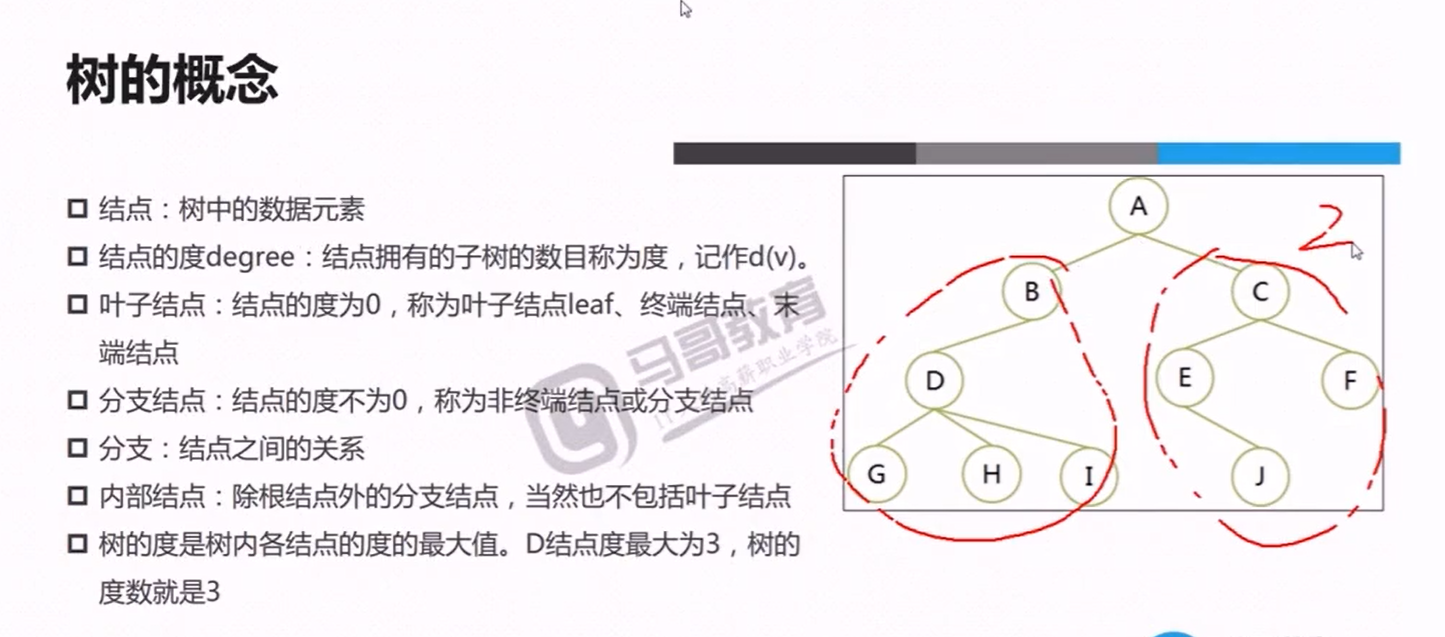
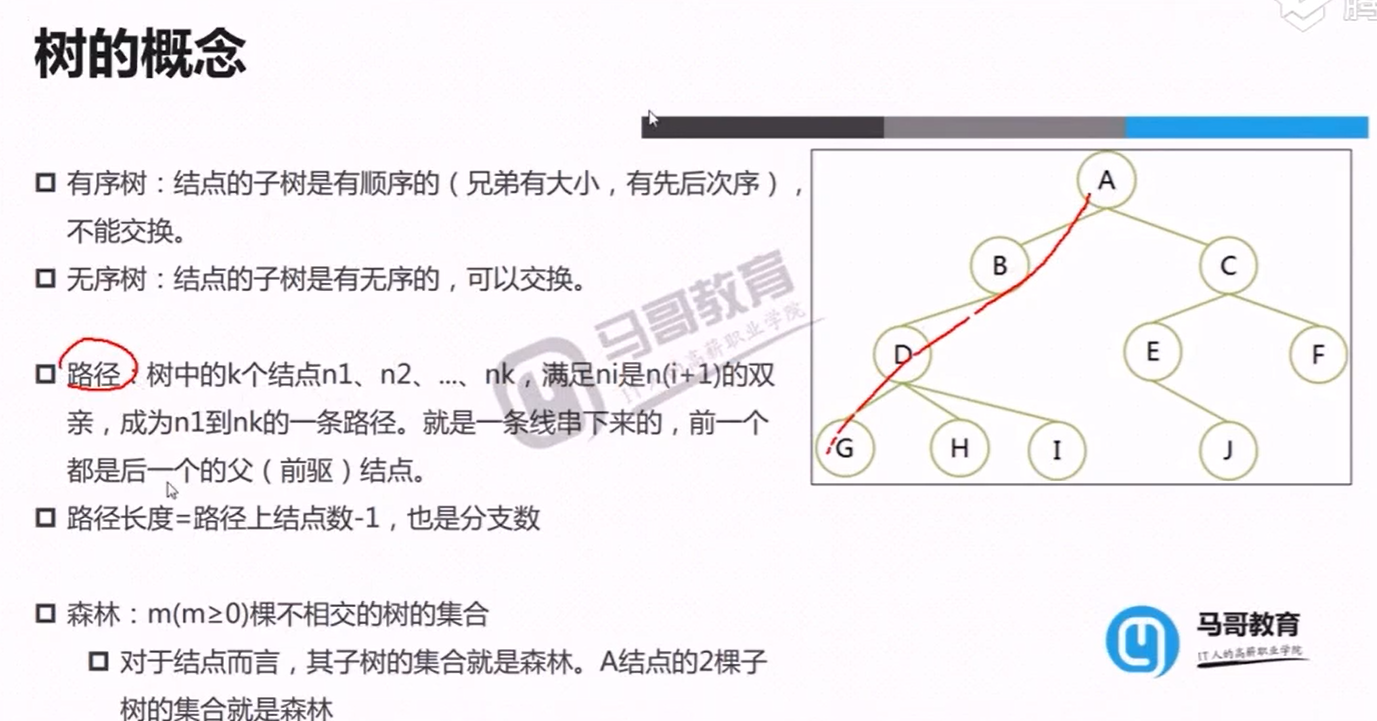
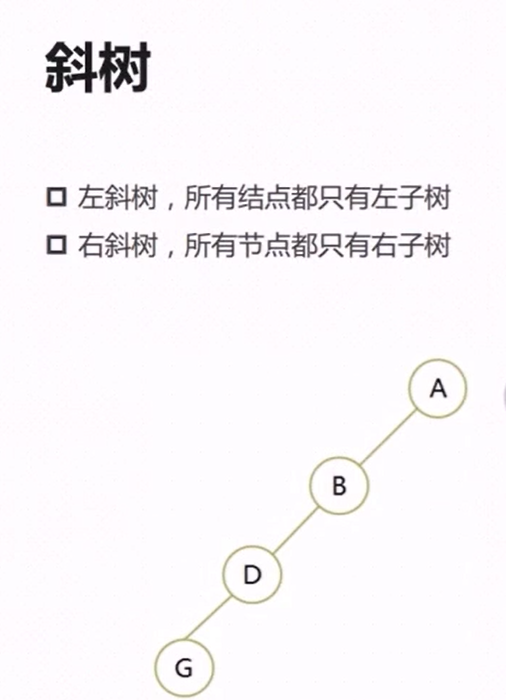
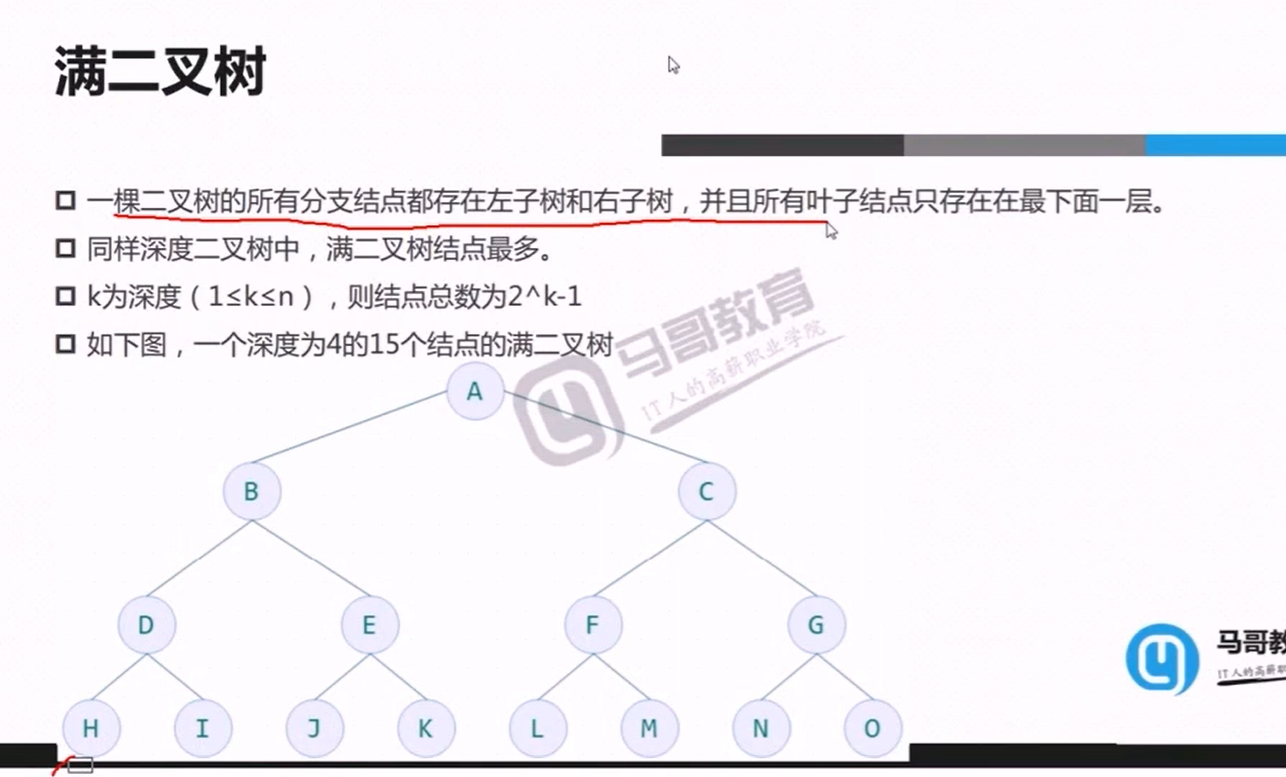
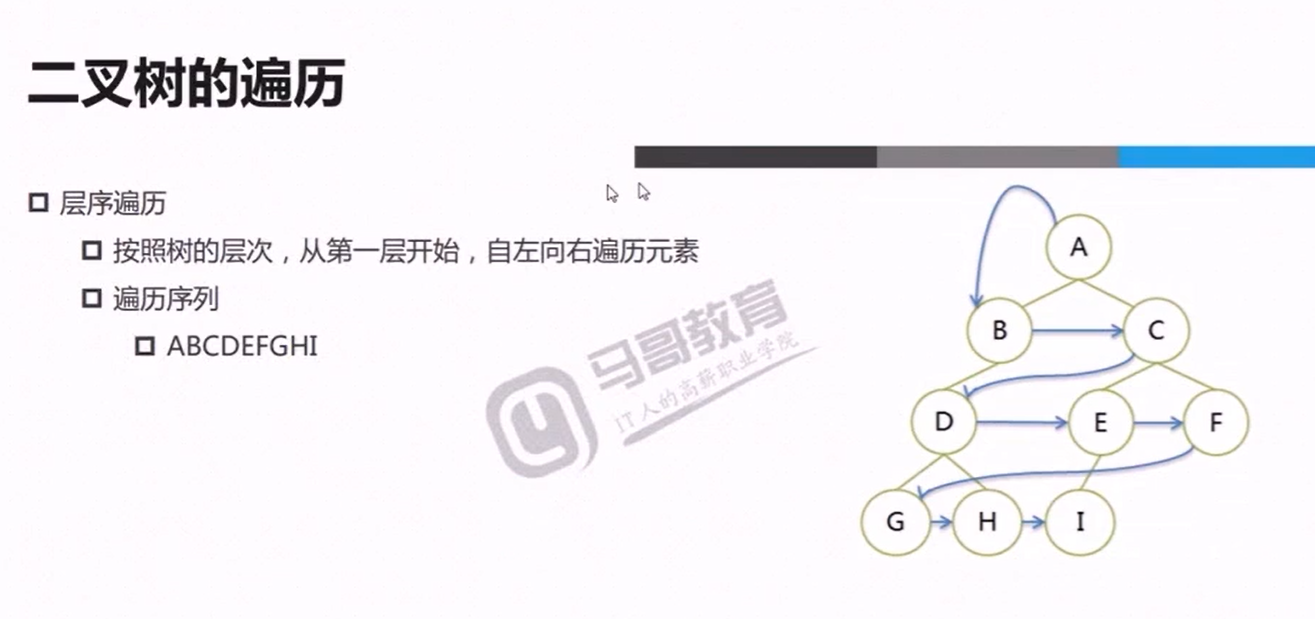
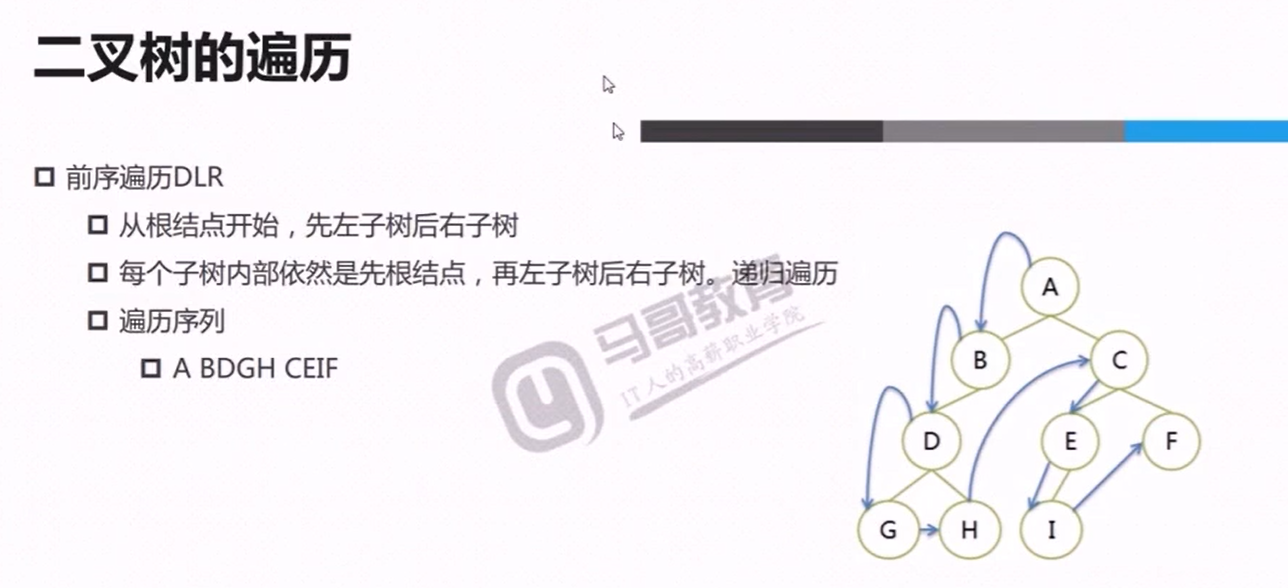
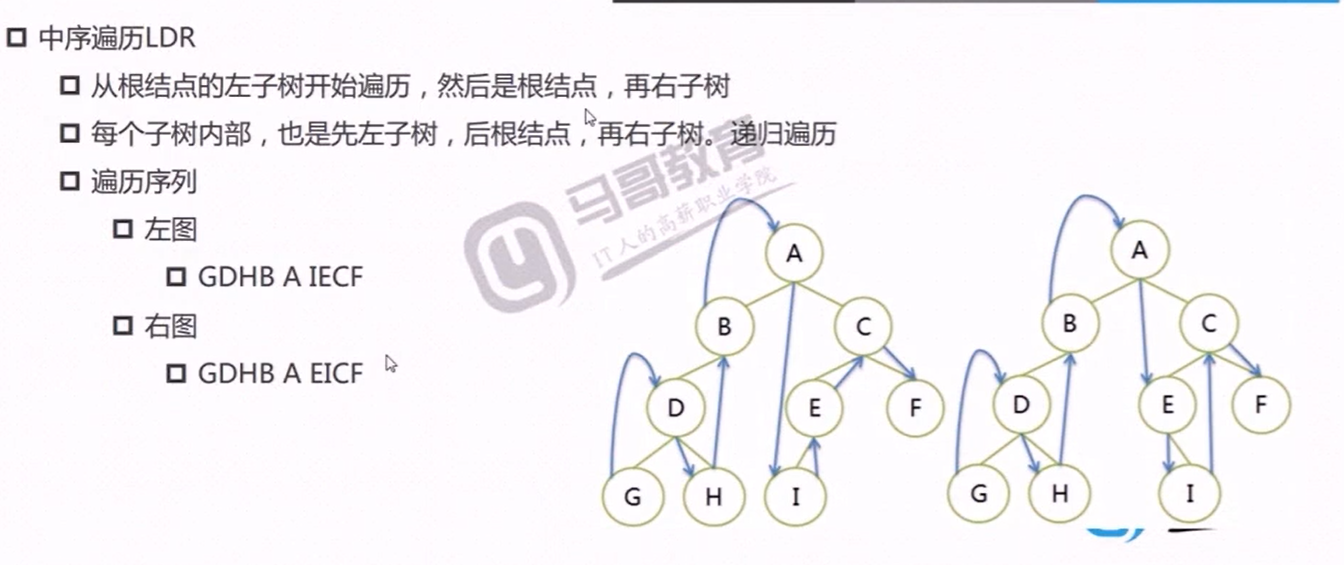
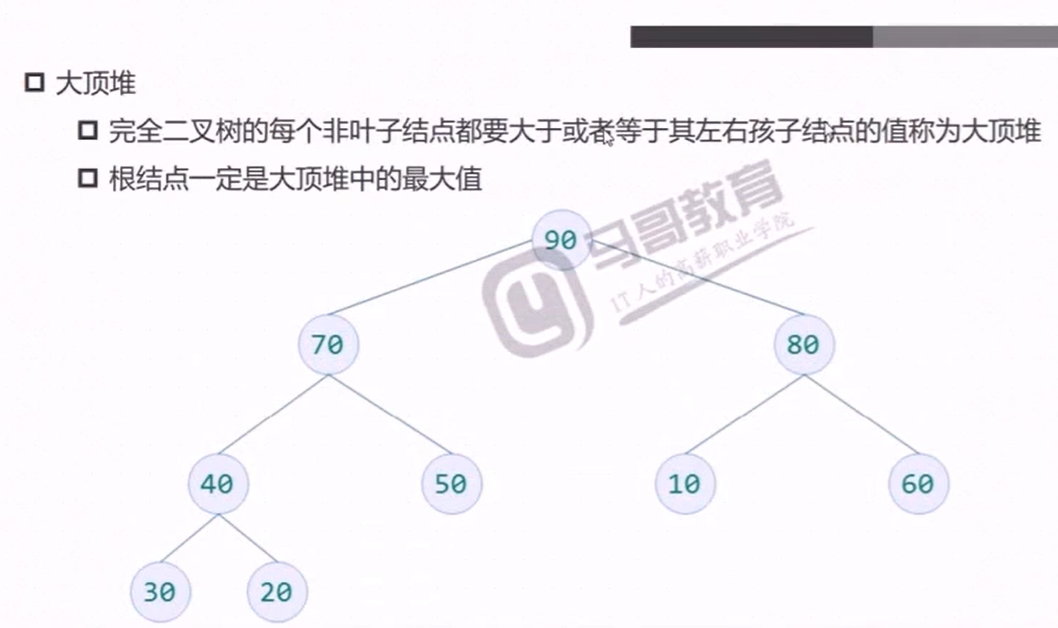
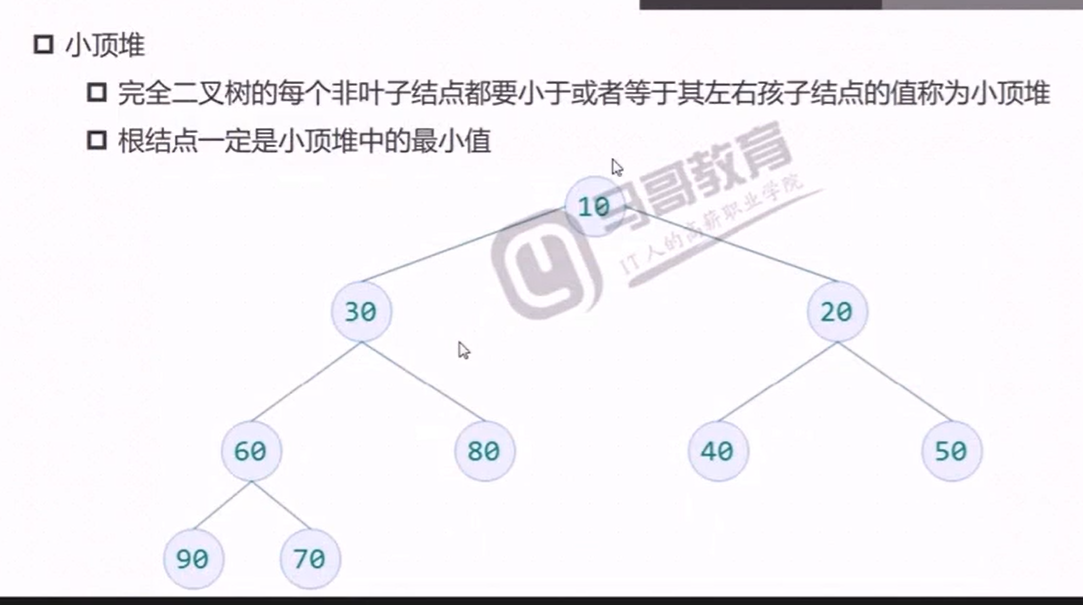
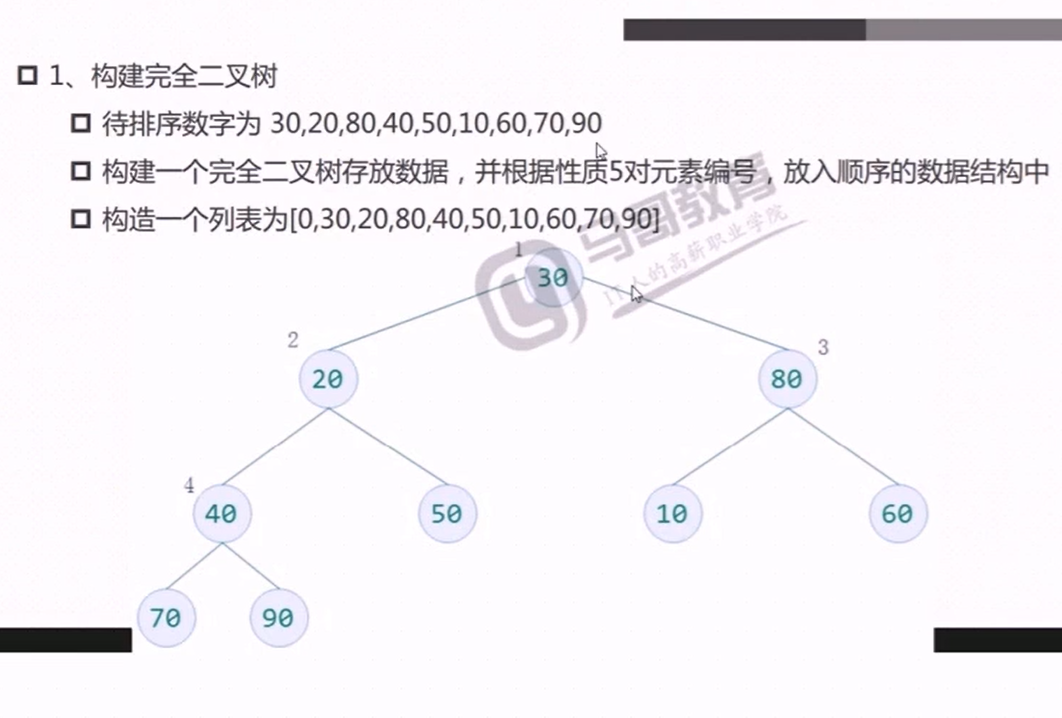
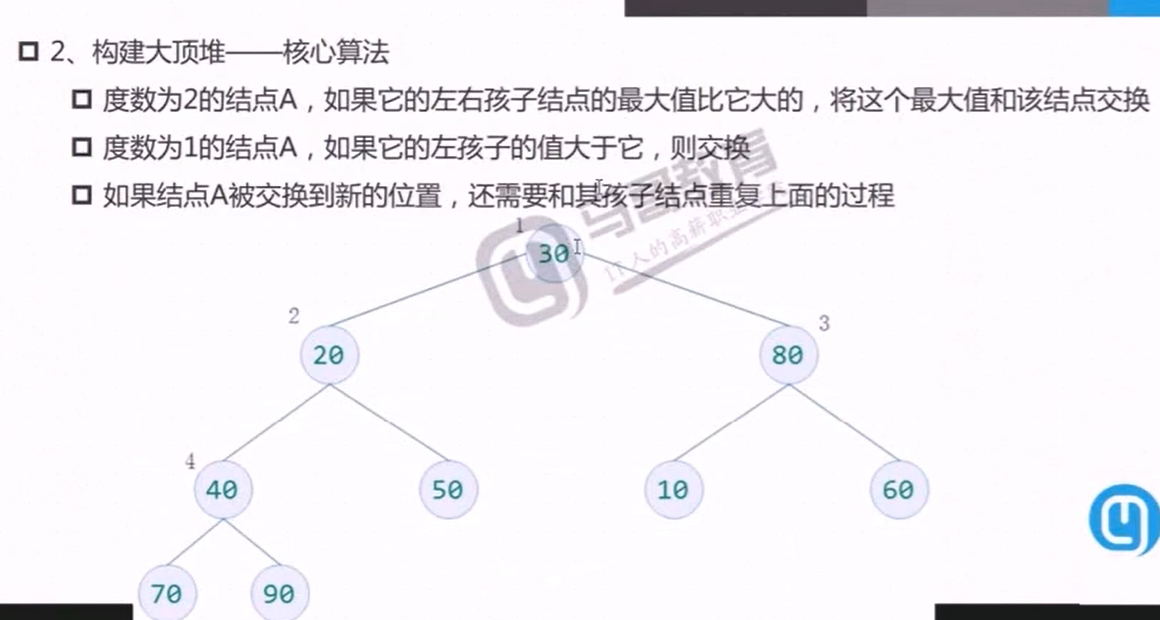
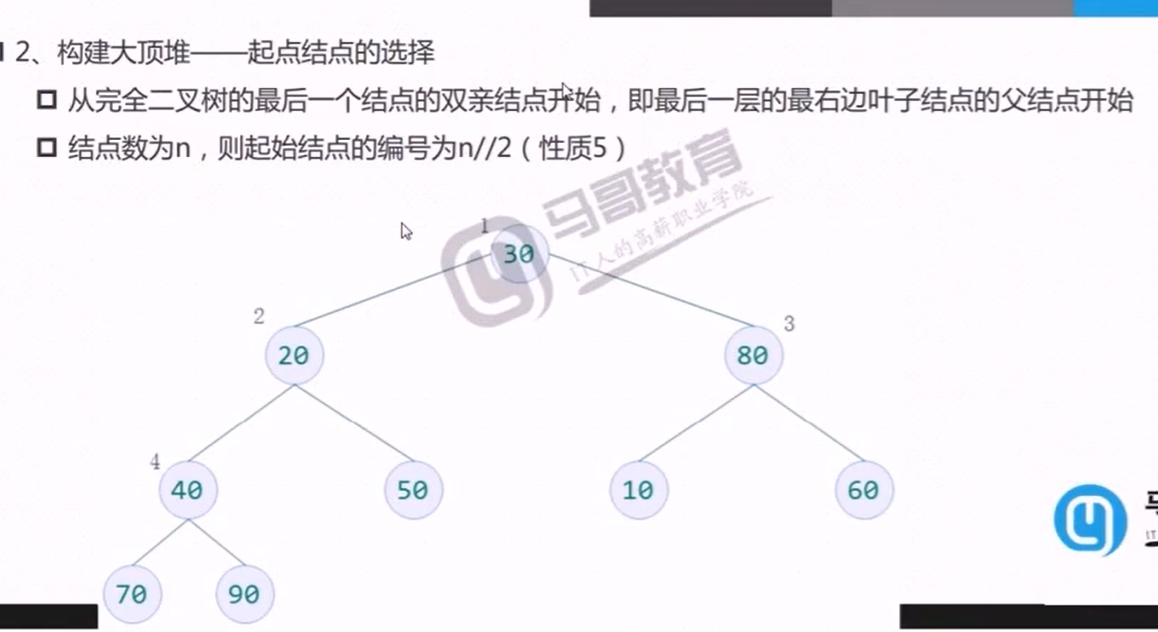
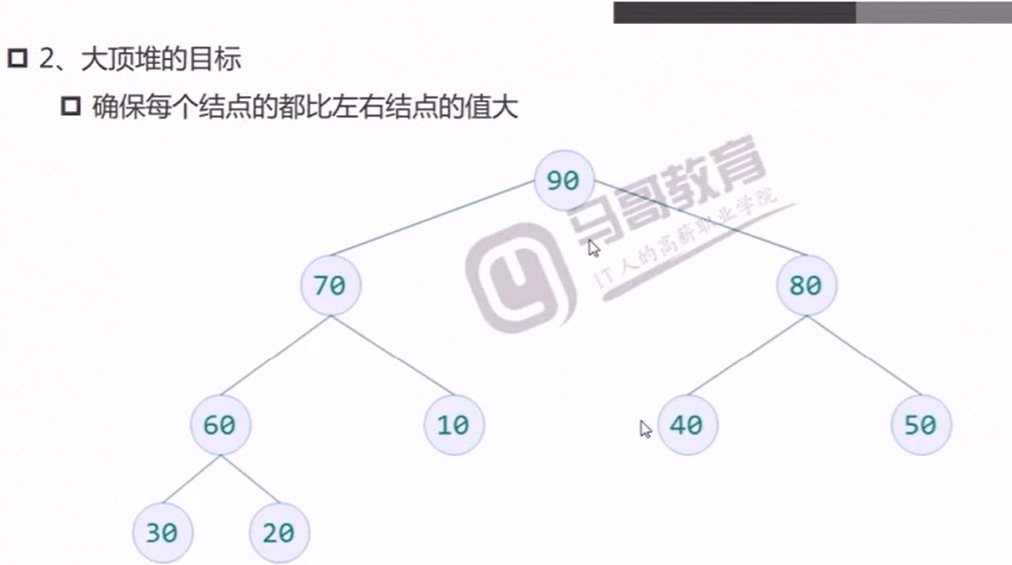
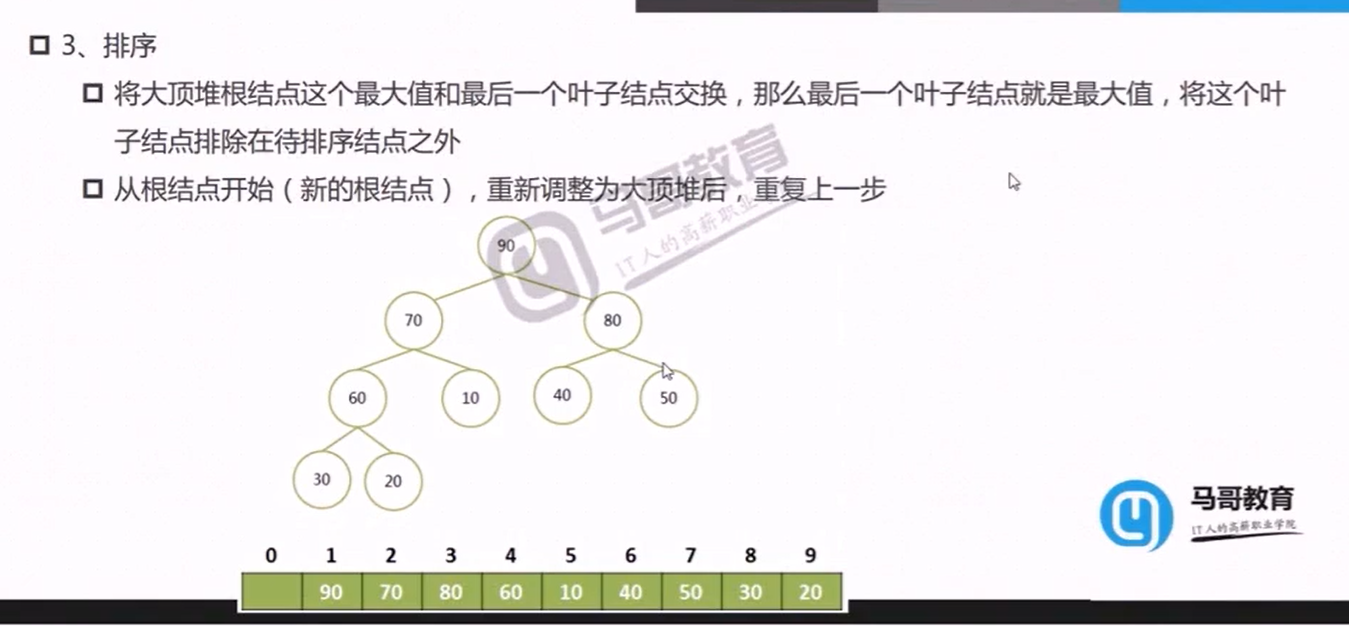
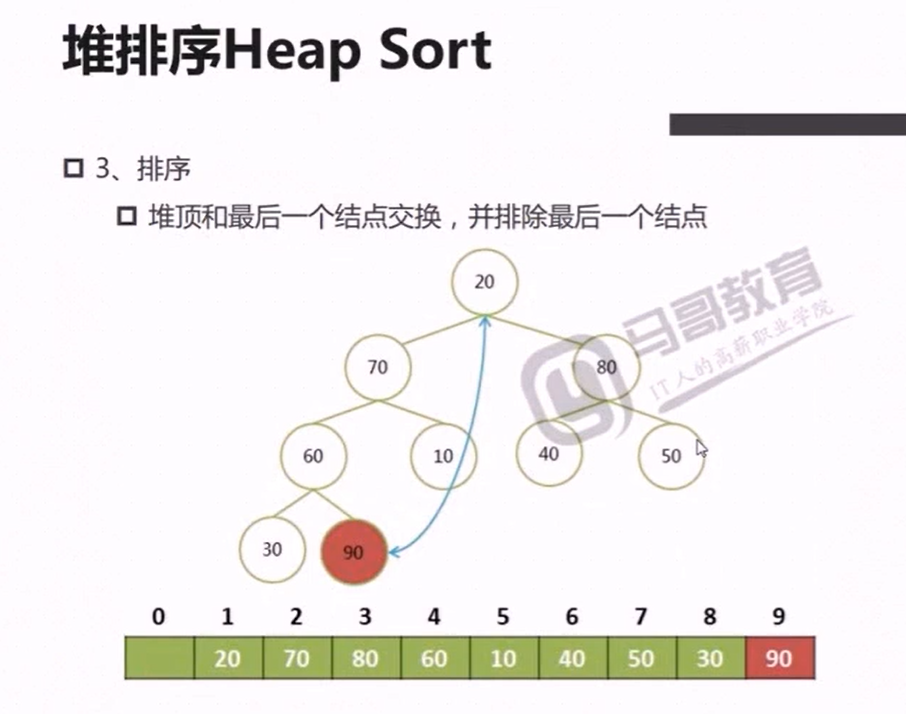
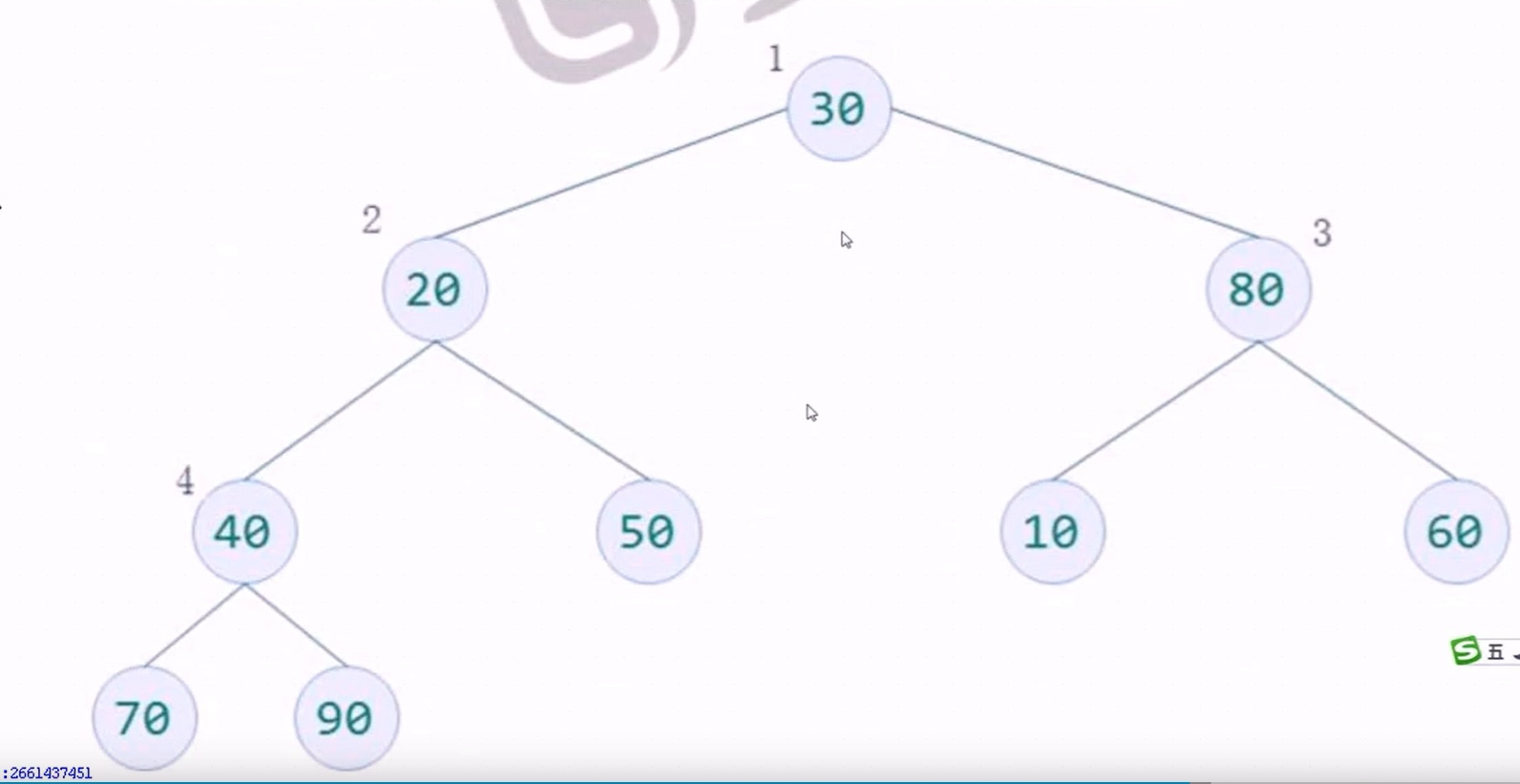
构建大顶堆测试代码

import e

# vail = [30, 20, 80, 40, 50, 10, 60, 70, 90]
vail = [30, 20, 80, 40, 50, 10, 10, 70, 90]  # 测试 break
vail.insert(0, 0)

total = len(vail[1:])

print(total, total // 2)

print(f'{"~" * 10}Initial State{"~" * 10}')
e.reveal(vail[1:])
print('{0}Initial State{0}'.format("~" * 10))


def heapify(n, i, vale: list):
    """
    heapify current node
    调整的起点在 n//2, 保证所有待调整节点都有孩子节点
    :param n: 待比较个数
    :param i: 当前节点下标
    :param vale: 待排序数据
    :return: None
    """

    while 2 * i <= n:  # 2*i==n or 2*i+1==n
        left_child_index = 2 * i
        max_child_index = left_child_index

        # n > left_child_index: n==2*i+1(存在右子树)
        if n > left_child_index and vale[left_child_index + 1] > vale[left_child_index]:
            max_child_index = left_child_index + 1

        if vale[max_child_index] > vale[i]:
            vale[i], vale[max_child_index] = vale[max_child_index], vale[i]
            i = max_child_index
            e.reveal(vale[1:])
        else:
            print('\nelse')
            e.reveal(vale[1:])
            break  # 因为已经构建完大顶堆, 故一旦 vale[i] > vale[max_child_index] 即可停止


# heapify(total, 1, vail)


def init_heap(vale: list):
    total = len(vale[1:])
    for i in range(total // 2, 0, -1):  # 从最后一个分支节点 -> 第一个分支节点 vale[1]
        print(f'i = {i}')
        heapify(total, i, vale)
    return vale


init_heap(vail)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

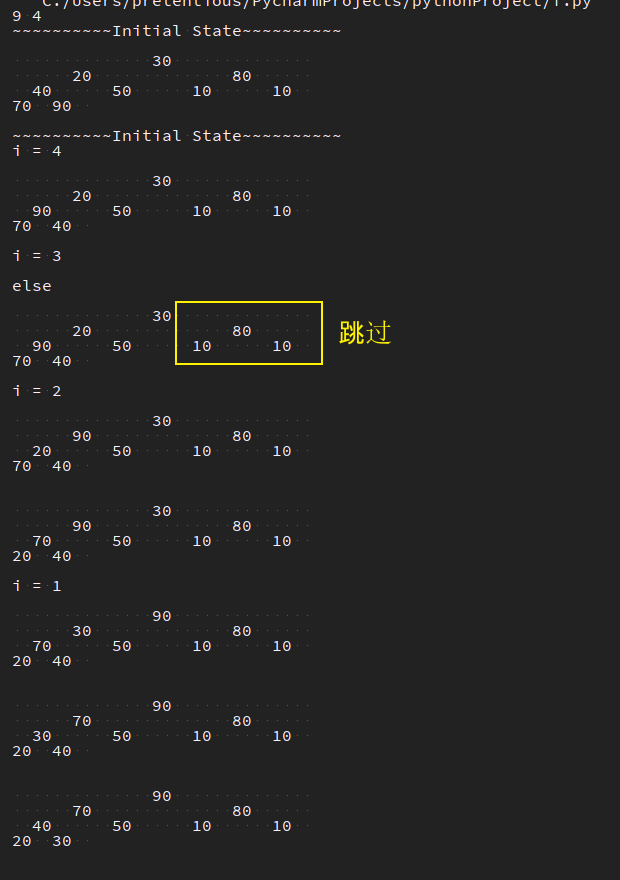
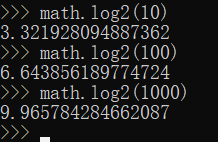
 跟树相关的 时间复杂度一个都有 log(n) , 一般前面还有n

n & log(n)

 

 

import math
from typing import Sequence


def reveal(vail: Sequence):
    """
    *** 假定元素是三位数以内的 ***
    length=len(vail) 元素个数
    2^k-1=length (Full Binary Tree)
    树高: height=math.ceil(math.log2(length+1))
    width: 2^height-1 所有元素排在一行的宽度
    最后一行元素个数: final=length-(2^(height-1)-1)
    每行元素个数:
    for b in range(1, height+1):
        n=2**(b-1)
        if b == height:
            return final
        else:
            return n
    一个元素会产生2个interval space, 从第二行开始还要保留上面行的元素位置(递归)
    每行组成:       space_size=(width-(2^height-1)) / intervals
    height  nodes  intervals  space_size
      1      1       2        (15-1) / 2   = 7
      2      2       4        (15-3) / 4   = 3
      3      4       8        (15-7) / 8   = 1
      4      8       16       (15-15) / 16 = 0
    :param vail:
    :return:
    """

    length = len(vail)
    height = math.ceil(math.log2(length + 1))
    width = 2 ** height - 1
    final = length - (2 ** (height - 1) - 1)
    print(f'height: {height}')
    print(f'width: {width}')
    print(f'final: {final}')
    print()

    index = 0  # 记录元素在vail的位置
    space = ' ' * 2  # 假定元素的是三位数以内, 宽度为2

    for b in range(1, height + 1):
        if b == height:
            nodes = final  # nodes 每行元素个数
        else:
            nodes = 2 ** (b - 1)

        space_size = int((width - (2 ** b - 1)) / (2 * nodes))  # 需要为int, 才能进行space * space_size
        # space_size = (width - (2 ** h - 1)) // (nodes * 2)

        # print(f'height: {b}')
        # print(f'current nodes: {nodes}')
        # print(f'total nodes: {2 ** b - 1}')
        # print(f'space_size: {space_size}')

        for node in range(nodes):
            if b == height and node > final - 1:  # 也可在index += 1 判断
                break
            if node == nodes - 1:  # 每行最后一个node
                print(f'{space * space_size}{vail[index]:0>2}{space * space_size}', end='')  # 最后一个元素无须补上一行的元素
            else:
                print(f'{space * space_size}{vail[index]:0>2}{space * space_size}', end=' ' * 2)  # 空格为了补上一行元素位置
            index += 1
            # if index > length - 1:
            #     break

        print()  # 可注释, 在node == nodes - 1最后一个元素位置直接打印换行


reveal(range(1, 20))

 

 

import e

# vail = [30, 20, 80, 40, 50, 10, 60, 70, 90]
vail = [30, 20, 80, 40, 50, 10, 10, 70, 90]  # 测试 break
vail.insert(0, 0)

total = len(vail[1:])

print(total, total // 2)

print(f'{"~" * 10}Initial State{"~" * 10}')
e.reveal(vail[1:])
print('{0}Initial State{0}'.format("~" * 10))


def heapify(n, i, vale: list):
    """
    heapify current node
    调整的起点在 n//2, 保证所有待调整节点都有孩子节点
    :param n: 待比较个数
    :param i: 当前节点下标
    :param vale: 待排序数据
    :return: None
    """

    while 2 * i <= n:  # 2*i==n or 2*i+1==n
        left_child_index = 2 * i
        max_child_index = left_child_index

        # n > left_child_index: n==2*i+1(存在右子树)
        if n > left_child_index and vale[left_child_index + 1] > vale[left_child_index]:
            max_child_index = left_child_index + 1

        if vale[max_child_index] > vale[i]:
            vale[i], vale[max_child_index] = vale[max_child_index], vale[i]
            i = max_child_index
            e.reveal(vale[1:])
        else:
            print('\nelse')
            e.reveal(vale[1:])
            break  # 因为已经构建完大顶堆, 故一旦 vale[i] > vale[max_child_index] 即可停止


# heapify(total, 1, vail)


def init_heap(vale: list):
    total = len(vale[1:])
    for i in range(total // 2, 0, -1):  # 从最后一个分支节点 -> 第一个分支节点 vale[1]
        print(f'i = {i}')
        heapify(total, i, vale)
    return vale


init_heap(vail)

print('{0}Heap sort{0}'.format('~' * 10))


def heap_sort(vale: list):
    total = len(vale[1:])
    while total > 1:
        vale[1], vale[total] = vale[total], vale[1]
        print('{0}After Swap{0}'.format('~' * 20))
        e.reveal(vale[1:])
        print('{0}After Swap XXX{0}'.format('~' * 20))
        print('\n' * 2)
        total -= 1
        if total == 2 and vale[total] >= vale[total - 1]:  # total-1==1
            break
        heapify(total, 1, vale)
    return vale[1:]


vail = heap_sort(vail)
print(vail)

 

import c

tug = [30, 20, 80, 40, 50, 10, 60, 70, 90]


def tinker(length: int, node: int, vale: list) -> None:
    """
    大顶堆单节点向下调整算法 root: i, left child: 2*i+1, right child: 2*i+2
    :param length: 待排序列表长度
    :param node: 需调整的节点
    :param vale: 需排序的列表
    :return: None
    """

    while 2 * node + 1 < length:  # 存在左孩子进行调整, 不存在左孩子时, 调整到了叶子节点, 循环结束
        if 2 * node + 2 < length and vale[2 * node + 2] > vale[2 * node + 1]:  # 存在右孩子 且 右孩子大于左孩子
            max_child_index = 2 * node + 2
        else:
            max_child_index = 2 * node + 1

        if vale[max_child_index] > vale[node]:  # 左右孩子大于其根节点, 进行交换
            vale[node], vale[max_child_index] = vale[max_child_index], vale[node]
            node = max_child_index  # 隐式递归, 对交换后的叶子节点继续调整
            c.reveal(vale)
        else:  # 根节点比children都大时, node没有进行调整, 需跳出循环
            print(f'\ntinker done, node >>{node}<< is bigger than children')
            c.reveal(vale)
            break


print(f'{"~" * 20}Initial State{"~" * 20}')
c.reveal(tug)
print('{0}Initial State{0}'.format('~' * 20))


def heapify(vale: list):
    n = ((len(vale) - 1) - 1) // 2  # 最后一个非叶子节点, 即最后一个叶子节点的父节点, 从此处开始倒序->0, 调整为大顶堆
    for i in range(n, -1, -1):
        tinker(len(vale), i, vale)


def heap_sort(vale: list):
    heapify(vale)  # 调整为大顶堆
    print(f'{"~" * 20}Max Heap{"~" * 20}')
    c.reveal(vale)
    print('{0}Max Heap{0}'.format('~' * 20))
    length = len(vale)
    while length > 1:
        vale[0], vale[length - 1] = vale[length - 1], vale[0]  # 交换堆顶和最后一个元素
        print('{0}After Swap{0}'.format('~' * 20))
        c.reveal(vale)
        print('{0}After Swap XXX{0}'.format('~' * 20))
        print('\n' * 2)
        length -= 1  # 堆变小
        if length == 2 and vale[length - 1] > vale[length - 2]:
            break
        tinker(length, 0, vale)  # 对交换后的堆, 从堆顶继续调整为大顶堆


heap_sort(tug)

print(tug)

 

交换过程

C:\Users\pretentious\PycharmProjects\pythonProject\venv\Scripts\python.exe C:/Users/pretentious/PycharmProjects/pythonProject/f.py
9 4
~~~~~~~~~~Initial State~~~~~~~~~~

              30              
      20              80      
  40      50      10      10  
70  90  

~~~~~~~~~~Initial State~~~~~~~~~~
i = 4

              30              
      20              80      
  90      50      10      10  
70  40  

i = 3

else

              30              
      20              80      
  90      50      10      10  
70  40  

i = 2

              30              
      90              80      
  20      50      10      10  
70  40  


              30              
      90              80      
  70      50      10      10  
20  40  

i = 1

              90              
      30              80      
  70      50      10      10  
20  40  


              90              
      70              80      
  30      50      10      10  
20  40  


              90              
      70              80      
  40      50      10      10  
20  30  

~~~~~~~~~~Heap sort~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~After Swap~~~~~~~~~~~~~~~~~~~~

              30              
      70              80      
  40      50      10      10  
20  90  

~~~~~~~~~~~~~~~~~~~~After Swap XXX~~~~~~~~~~~~~~~~~~~~




              80              
      70              30      
  40      50      10      10  
20  90  


else

              80              
      70              30      
  40      50      10      10  
20  90  

~~~~~~~~~~~~~~~~~~~~After Swap~~~~~~~~~~~~~~~~~~~~

              20              
      70              30      
  40      50      10      10  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap XXX~~~~~~~~~~~~~~~~~~~~




              70              
      20              30      
  40      50      10      10  
80  90  


              70              
      50              30      
  40      20      10      10  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap~~~~~~~~~~~~~~~~~~~~

              10              
      50              30      
  40      20      10      70  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap XXX~~~~~~~~~~~~~~~~~~~~




              50              
      10              30      
  40      20      10      70  
80  90  


              50              
      40              30      
  10      20      10      70  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap~~~~~~~~~~~~~~~~~~~~

              10              
      40              30      
  10      20      50      70  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap XXX~~~~~~~~~~~~~~~~~~~~




              40              
      10              30      
  10      20      50      70  
80  90  


              40              
      20              30      
  10      10      50      70  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap~~~~~~~~~~~~~~~~~~~~

              10              
      20              30      
  10      40      50      70  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap XXX~~~~~~~~~~~~~~~~~~~~




              30              
      20              10      
  10      40      50      70  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap~~~~~~~~~~~~~~~~~~~~

              10              
      20              10      
  30      40      50      70  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap XXX~~~~~~~~~~~~~~~~~~~~




              20              
      10              10      
  30      40      50      70  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap~~~~~~~~~~~~~~~~~~~~

              10              
      10              20      
  30      40      50      70  
80  90  

~~~~~~~~~~~~~~~~~~~~After Swap XXX~~~~~~~~~~~~~~~~~~~~



[10, 10, 20, 30, 40, 50, 70, 80, 90]

Process finished with exit code 0