Problem Set 4
Problem Set 4.1
Problem 4.1.1
首先判断\(A[1]\)和\(A[n]\)是不是峰值,如果是的话就找到了,如果都不是的话就说明数列在开头一段处于单调递增的状态,末尾一段处于单调递减的状态,于是可以知道在\([2,n-1]\)中一定存在峰值。接下来使用二分,设当前在区间\([l,r]\)中存在答案(初始化\(l=1,r=n\))并且这个区间中开头一段单调递增末尾一段单调递减,令\(mid=\lfloor\frac{l+r}{2}\rfloor\),如果\(A[mid]\)是峰值,就找到了,否则是如下三种情况
- \(A[mid-1]<A[mid]<A[mid+1]\),此时在\([mid,r]\)这段区间中一定存在答案(因为这段区间开头一段单调递增末尾一段单调递减),令\(l=mid\)
- \(A[mid-1]>A[mid]>A[mid+1]\),此时在\([l,mid]\)这段区间中一定存在答案(因为这段区间开头一段单调递增末尾一段单调递减),令\(r=mid\)
- \(A[mid-1]>A[mid]<A[mid+1]\),这是令\(l=mid\)或\(r=mid\)都行
综上,时间复杂度为\(O(\log n)\)
def find_peak(nums):
n = len(nums)
if n == 1:
return 0
if nums[0] > nums[1]:
return 0
if nums[-1] > nums[-2]:
return n - 1
left, right = 1, n - 2
while left <= right:
mid = (left + right) // 2
if nums[mid] > nums[mid - 1] and nums[mid] > nums[mid + 1]:
return mid
elif nums[mid - 1] < nums[mid] < nums[mid + 1]:
left = mid + 1
elif nums[mid - 1] > nums[mid] > nums[mid + 1]:
right = mid - 1
else:
left = mid + 1
Problem 4.1.2
\((1)\)不平衡,反例如下
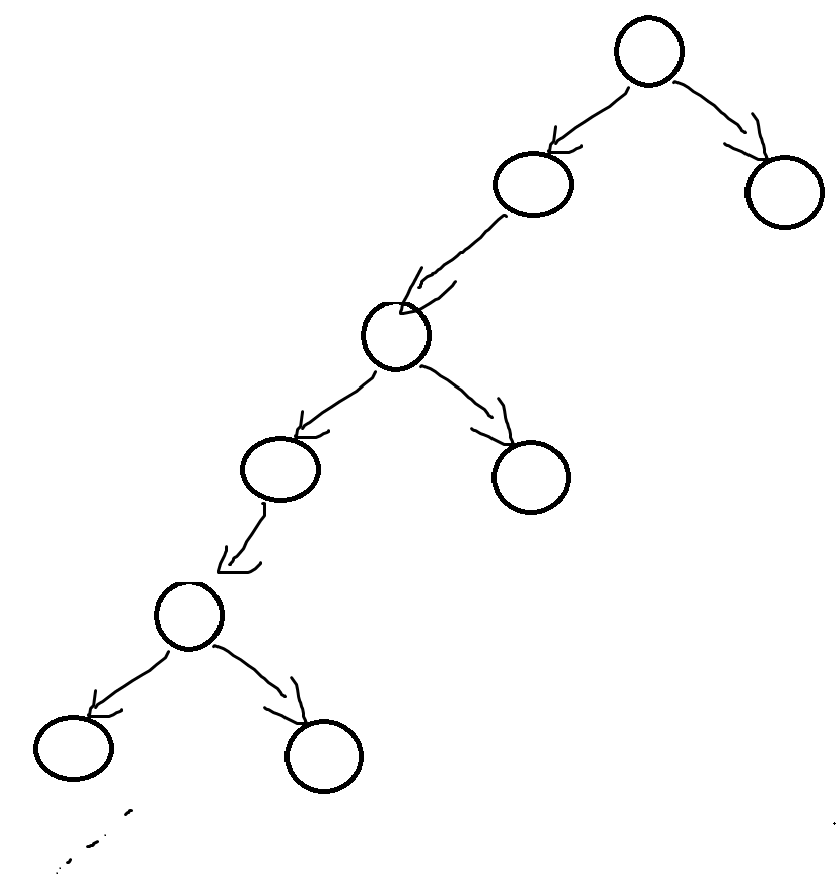
\((2)\)平衡,按照\(k\)归纳(归纳更强的结论:当二叉树满足题述性质的时候,二叉树一定是满二叉树)
当\(k=0\)的时候,此时没有节点,显然是一个满二叉树
当\(\forall k<c\)的时候树都是满二叉树的,那么当\(k=c\)的时候,设根节点的两个儿子的大小分别为\(2^{k_1}-1,2^{k_2}-1(k_1,k_2∈\mathbb{N})\),则有\(2^k-1=2^{k_1}-1+2^{k_2}-1+1=2^{k_1}+2^{k_2}-1\).根据二进制数的性质,\(2^k\)的二进制表示只有一个\(1\),而如果\(k_1≠k_2\),那么\(2^{k_1}+2^{k_2}\)的二进制表示下有两个\(1\),所以\(k_1=k_2=k-1\).根据数学归纳,两棵子树都是满二叉树,而且两棵子树的大小是相同的,所以两个子树一模一样,在加上根节点可知,整棵树是一个满二叉树,当然也就平衡了
\((3)\)平衡。假设一共有\(n\)个节点,那么根节点的较大子树的大小不会超过\(\frac{n-1}{1+c}\),于是有\(H(n)\leq 1+H(\frac{n-1}{1+c})\leq1+1+H(\frac{n-1}{(1+c)^2})\leq...\),所以节点以指数级别缩小,于是可以知道平衡(注意\(\Theta(\log_p n)=\Theta(\frac{\log_q n}{\log_q p})=\Theta(\log_q n)\))
4.1.3
利用数学归纳法
- \(T\)为\(RB_h\)的情况:
- 当\(h=0\)的时候,显然都满足
- 当\(\forall h<c\)的时候都满足,则当\(h=c\)的时候,考虑根的两个儿子的情况
- 两个儿子都是\(RB_{h-1}\)
- \(T\)至少有\(2\times(2^{h-1}-1)+1=2^h-1\)个内部黑节点
- \(T\)至多有\(2\times(4^{h-1}-1)+1\lt 4^h-1\)个内部节点
- 要证明性质三,只需要证明根节点的深度最多是\(T\)的black depth的两倍。此时根节点的深度是两个儿子节点深度更大者加一,而\(T\)的black depth是任意一个儿子节点的black depth加一,于是不难证明
- 两个儿子一个是\(RB_{h-1}\),另一个是\(ARB_{h}\)
- 由于\(ARB_{h}\)的两个儿子都是\(RB_{h-1}\),于是\(T\)至少有\(2^{h-1}-1+2\times(2^{h-1}-1)+1\gt 2^h-1\)个内部黑节点
- 由于\(ARB_{h}\)的两个儿子都是\(RB_{h-1}\),于是\(T\)至多有\(4^{h-1}-1+2\times(4^{h-1}-1)+2\lt 4^h-1\)个内部节点
- 要证明性质三,只需要证明根节点的深度最多是\(T\)的black depth的两倍。此时根节点的深度是两个儿子节点深度更大者加一,而\(T\)的black depth是任意一个儿子节点的black depth加一(注意其中一个节点是红色根节点,所以不影响这个结论),于是不难证明
- 两个儿子都是\(ARB_{h}\)
- \(T\)至少有\(4\times(2^{h-1}-1)+1\gt2^h-1\)个内部黑节点
- \(T\)至多有\(4\times(4^{h-1}-1)+3=4^h-1\)个内部节点
- 要证明性质三,只需要证明根节点的深度最多是\(T\)的black depth的两倍。此时根节点的深度是两个儿子节点深度更大者加一,而\(T\)的black depth是任意一个儿子节点的black depth加一,于是不难证明
- 两个儿子都是\(RB_{h-1}\)
- \(A\)为\(ARB_{h}\)的情况:
- \(A\)至少有\(2\times(2^{h-1}-1)=2^h-2\)个内部黑节点
- \(A\)至多有\(2\times(4^{h-1}-1)+1=\frac{4^h}{2}-1\)个内部节点
- 由上文证明\(RB_{h}\)的第三条性质可知成立
Problem Set 4.2
Problem 4.2.1
\((1)\)\(h_1(72)=6\),插入;\(h_1(11)=0\),插入;\(h_1(42)=9\),插入;\(h_1(68)=2\),插入;\(h_1(6)=6\),插入;\(h_1(30)=8\),插入;\(h_1(47)=3\),插入;\(h_1(98)=10\),插入;\(h_1(10)=10\),插入。故最终的表如下(为了简便假设哈希表直接存链表头)
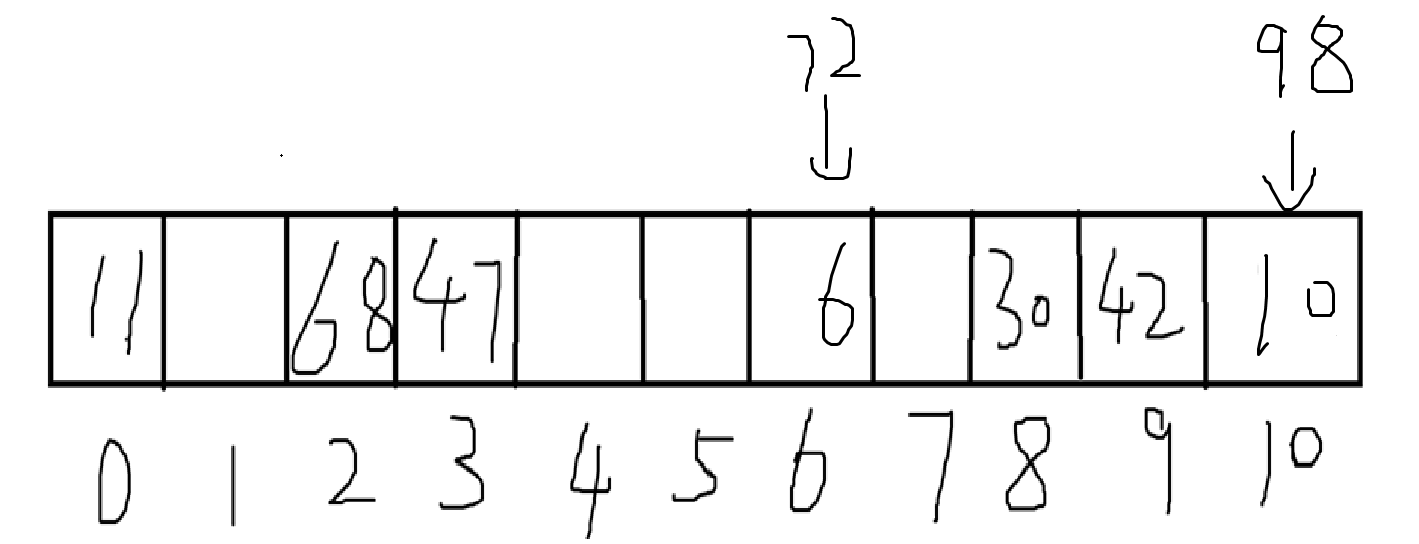
\((2)\)\(h_1(72)=6\),插入;\(h_1(11)=0\),插入;\(h_1(42)=9\),插入;\(h_1(68)=2\),插入;\(h_1(6)=6,h(6,1)=7\),插入;\(h_1(30)=8\),插入;\(h_1(47)=3\),插入;\(h_1(98)=10\),插入;\(h_1(10)=10,h(10,1)=0,h(10,2)=1\),插入。故最终表如下
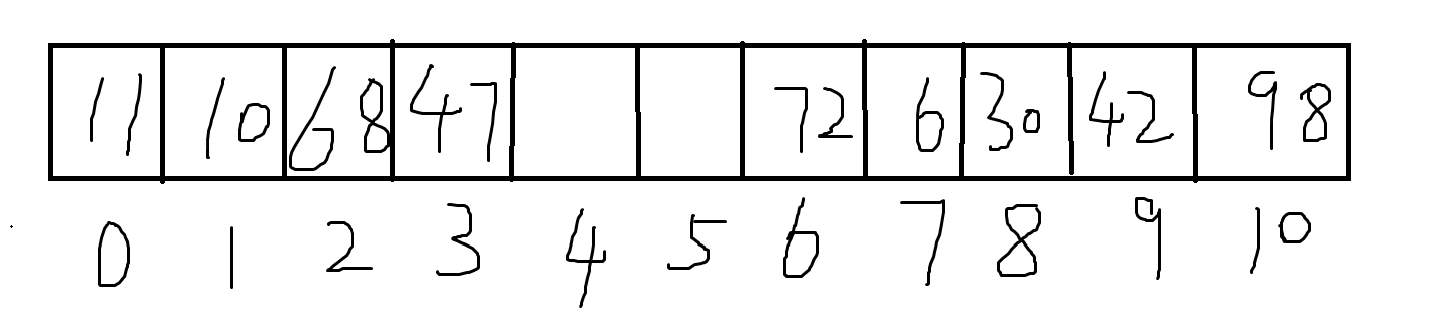
\((3)\)\(h_1(72)=6\),插入;\(h_1(11)=0\),插入;\(h_1(42)=9\),插入;\(h_1(68)=2\),插入;\(h_1(6)=6,h(6,1)=2,h(6,2)=9,h(6,3)=5\),插入;\(h_1(30)=8\),插入;\(h_1(47)=3\),插入;\(h_1(98)=10\),插入;\(h_1(10)=10,h(10,1)=0,h(10,2)=1\),插入。故最终表如下
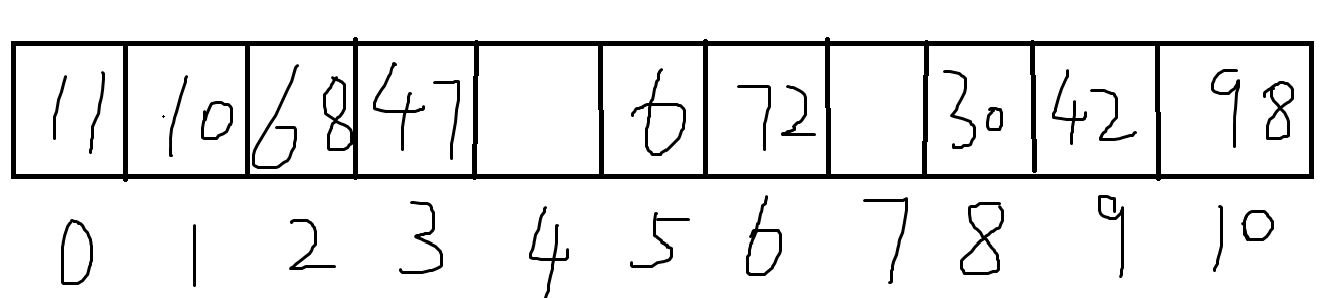
Problem 4.2.2
a.对于\(\alpha=0.25,0.5,1.0,2.0\)来说,closed addressing需要的空间分别为\(h_c+2n=h_c+2\alpha h_c=(1+2\alpha)h_c=1.5h_c,2h_c,3h_c,5h_c\);对应的空间分别用在open addrssing下,\(\alpha\)分别为\(\frac{\alpha h_c}{(1+2\alpha)h_c}=\frac{\alpha}{1+2\alpha}=\frac{1}{6},\frac{1}{4},\frac{1}{3},\frac{2}{5}\)
b.对于\(\alpha=0.25,0.5,1.0,2.0\)来说,closed addressing需要的空间分别为\(h_c+5n=h_c+5\alpha h_c=(1+5\alpha)h_c=2.25h_c,3.5h_c,6h_c,11h_c\);对应的空间分别用在open addrssing下,\(\alpha\)分别为\(\frac{\alpha h_c}{(1+5\alpha)h_c/4}=\frac{4\alpha}{1+5\alpha}=\frac{4}{9},\frac{4}{7},\frac{2}{3},\frac{8}{11}\)
Problem 4.2.3
假设符合一致哈希,那么有\(\frac{1}{1-\alpha}=2\cdot\frac{1}{\alpha}\ln\frac{1}{1-\alpha}\),解得\(\alpha\approx0.715\)
Problem Set 4.3
Problem 4.3.1
class UnionFind:
def __init__(self, size):
self.parent = list(range(size + 1))
self.size = [1] * (size + 1)
def find(self, x):
while self.parent[x] != x:
x = self.parent[x]
return x
def wUnion(self, a, b):
root_a = self.find(a)
root_b = self.find(b)
if root_a == root_b:
return
if self.size[root_a] < self.size[root_b]:
root_a, root_b = root_b, root_a
self.parent[root_b] = root_a
self.size[root_a] += self.size[root_b]
Problem 4.3.2
使用数学归纳法。对于\(k=0\)显然成立。假设对\(\forall k<c\)时都成立,对于\(k=c\)时,由\(T_k\)的构造方式可知,其节点数为\(2\times2^{k-1}=2^k\),高度为\(k-1+1=k\),在高度\(k\)只有一个节点,也就是\(T_{k-1}\)中高度为\(k-1\)的节点(因为被附加的\(T_{k-1}\)的所有节点的深度都加一,另一个\(T_{k-1}\)的所有节点的深度不变,而被附加的\(T_{k-1}\)只有一个节点的深度为\(k-1\))
Problem 4.3.3
建立\(n\)个点,对于每一个等于的约束,将等号两边的点用并查集合并;处理完所有等于约束之后,再依次检查每个不等于约束是否成立(不等号两边的元素如果在同一集合中就不成立),如果都成立那么就可以同时满足,否则就不行
class UnionFind:
def __init__(self, size):
self.parent = list(range(size))
self.rank = [0] * size
def find(self, x):
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, x, y):
root_x = self.find(x)
root_y = self.find(y)
if root_x == root_y:
return
if self.rank[root_x] < self.rank[root_y]:
self.parent[root_x] = root_y
else:
self.parent[root_y] = root_x
if self.rank[root_x] == self.rank[root_y]:
self.rank[root_x] += 1
def var_to_index(var):
return int(var[1:]) - 1
def can_satisfy_constraints(n, constraints):
uf = UnionFind(n)
inequalities = []
for constraint in constraints:
a, op, b = constraint.split()
if op == '=':
idx_a = var_to_index(a)
idx_b = var_to_index(b)
uf.union(idx_a, idx_b)
else:
inequalities.append((a, b))
for a, b in inequalities:
idx_a = var_to_index(a)
idx_b = var_to_index(b)
if uf.find(idx_a) == uf.find(idx_b):
return False
return True
Problem 4.3.4
时间复杂度为\(O(n)\)。均摊操作如下:在一次加法中,对于每个进位的位置(此时这些位置都是\(2\)),将其进位的复杂度摊到其前面最晚的一次从\(1\)变成\(2\)的时候
实际费用:\(t+1\)
会计费用:\(1-t\)(当且仅当当前加法操作涉及到的最高位为\(1\)的时候才会在\(-t\)前面加一)
均摊费用:\(2=O(1)\)
所以在实施\(n\)次操作之后,时间复杂度为\(O(n)\)
Problem 4.3.5
可以用一个链表来实现。对于插入操作,简单地插入就好了;对于删除操作,首先使用选择算法线性找出第\(\lceil\frac{|s|}{2}\rceil\)大,设为\(x\),然后遍历链表将严格大于\(x\)的数删掉,同时记录删除的数的个数,设为\(c\),然后再遍历链表,删除\(\lceil\frac{|s|}{2}\rceil-c\)个\(x\)即可。每次删除操作的\(O(n)\)时间复杂度可以均摊到被删除的数上,所以平摊代价为\(O(1)\).下面是均摊操作:
- 插入操作
- 实际费用:\(t_1\)(\(t_1\)是将元素插入到链表中的费用)
- 会计费用:\(t_2\)(\(t_2\)是某次删除操作中,当前插入的元素被删除了,那一次删除操作的总费用均摊到这个元素上面的费用)
- 均摊费用:\(t_1+t_2=O(1)\)
- 删除操作
- 实际费用:\(\frac{t_2}{2}|s|\)
- 会计费用:\(-\frac{t_2}{2}|s|\)(此时被删除的\(\lceil\frac{|s|}{2}\rceil\)个元素,每个元素均摊到的费用为\(t_2\))
- 均摊费用:\(0\)
class Node:
def __init__(self, value):
self.value = value
self.prev = None
self.next = None
class LinkedList:
def __init__(self):
self.head = None
self.tail = None
self.size = 0
def insert(self, value):
new_node = Node(value)
if self.head is None:
self.head = self.tail = new_node
else:
new_node.next = self.head
self.head.prev = new_node
self.head = new_node
self.size += 1
def to_list(self):
result = []
current = self.head
while current:
result.append(current.value)
current = current.next
return result
def delete_node(self, node):
if node.prev:
node.prev.next = node.next
else:
self.head = node.next
if node.next:
node.next.prev = node.prev
else:
self.tail = node.prev
self.size -= 1
def del_larger_half(ll):
if ll.size == 0:
return
k = (ll.size + 1) // 2
arr = ll.to_list()
x = 选择算法
to_delete = []
current = ll.head
while current:
if current.value > x:
to_delete.append(current)
current = current.next
for node in to_delete:
ll.delete_node(node)
deleted = len(to_delete)
if deleted < k:
remaining = k - deleted
current = ll.head
to_delete = []
while current and remaining > 0:
if current.value == x:
to_delete.append(current)
remaining -= 1
current = current.next
for node in to_delete:
ll.delete_node(node)






 浙公网安备 33010602011771号
浙公网安备 33010602011771号