第三课 反向传播与神经网络

对于文本标注问题，如果不适用BERT，而是使用一般神经网络，那么应该长成下面这个样子

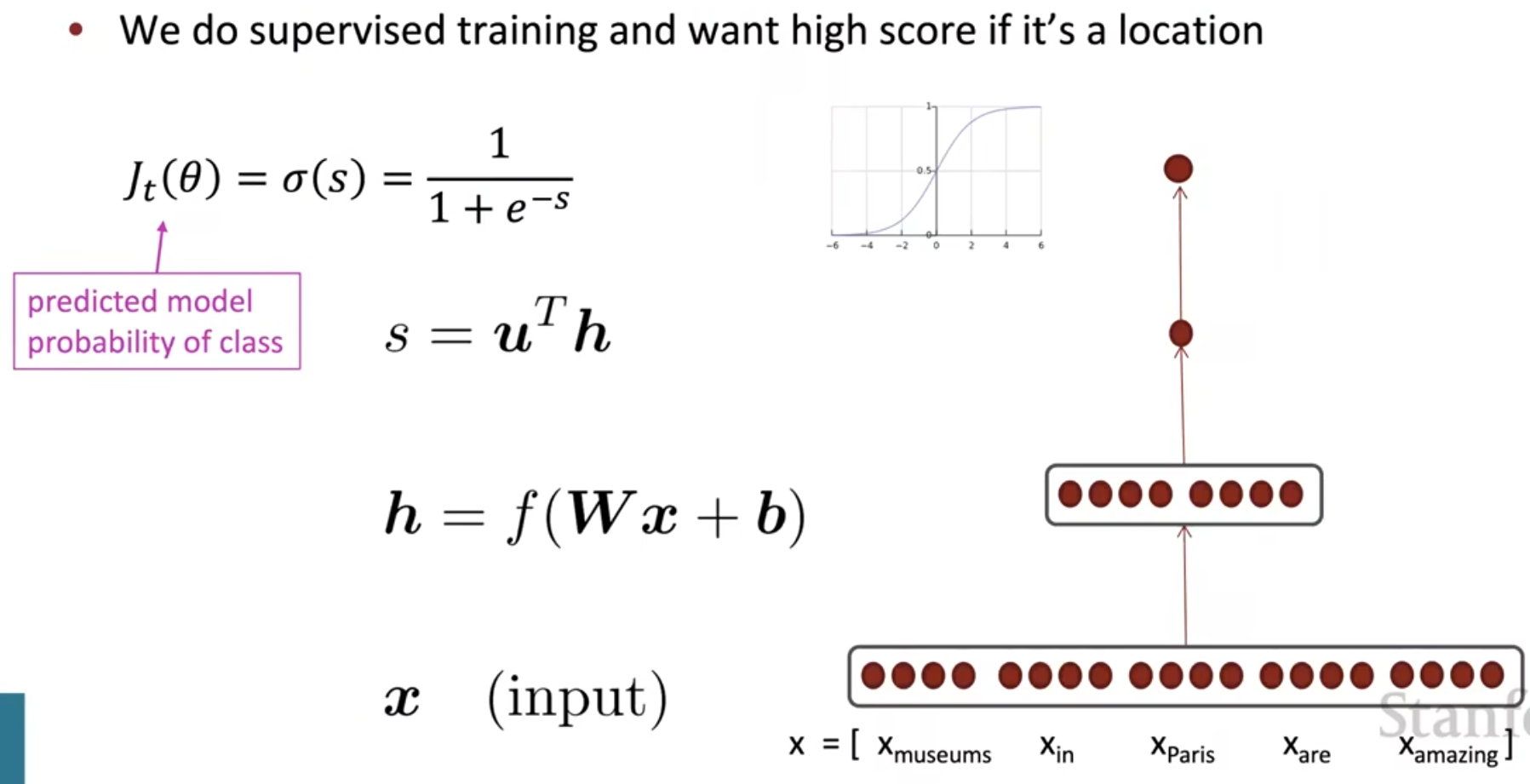
复习一下典型的神经网络反向传播的过程中求导的步骤

那个小圆圈是哈达姆积，想一下为什么可以这么转换
然后来看一下\(\frac{\partial{s}}{\partial{W}}\)，如下

所以我们不必进行重复运算，直接用一个变量存储下来


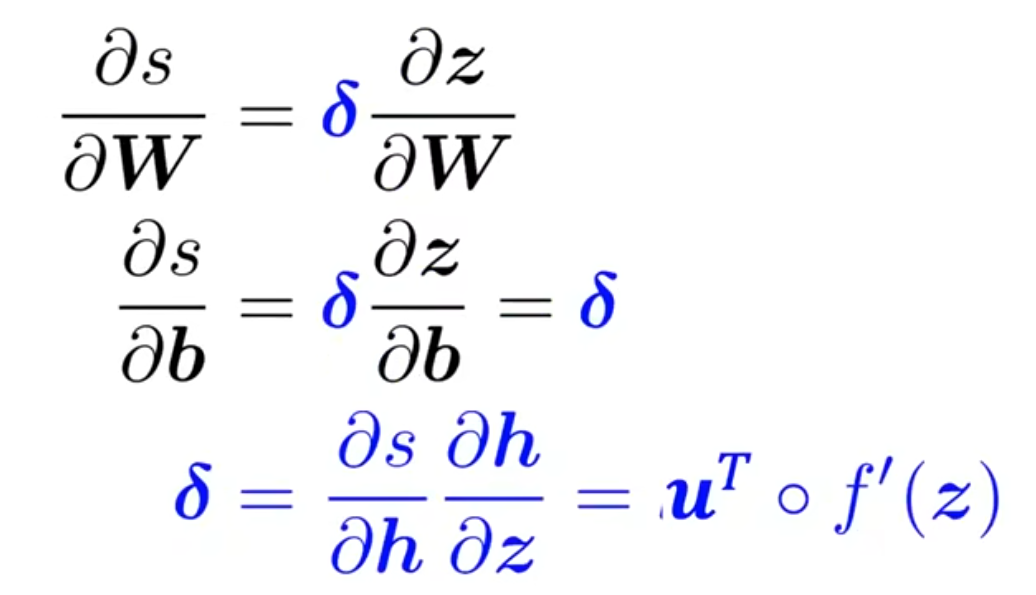
这里最终答案的形状很奇怪，是因为他跟我们的约定不同，我们就按照李沐的约定，最后算出来应该是\(x\delta\)（注意\(\delta\)是一个行向量）
虽然我们可以直接得到\(\frac{\partial{z}}{\partial{W}}=x\)然后再去调整形状，但是我们可以去认真计算一下前者到底为什么，如下

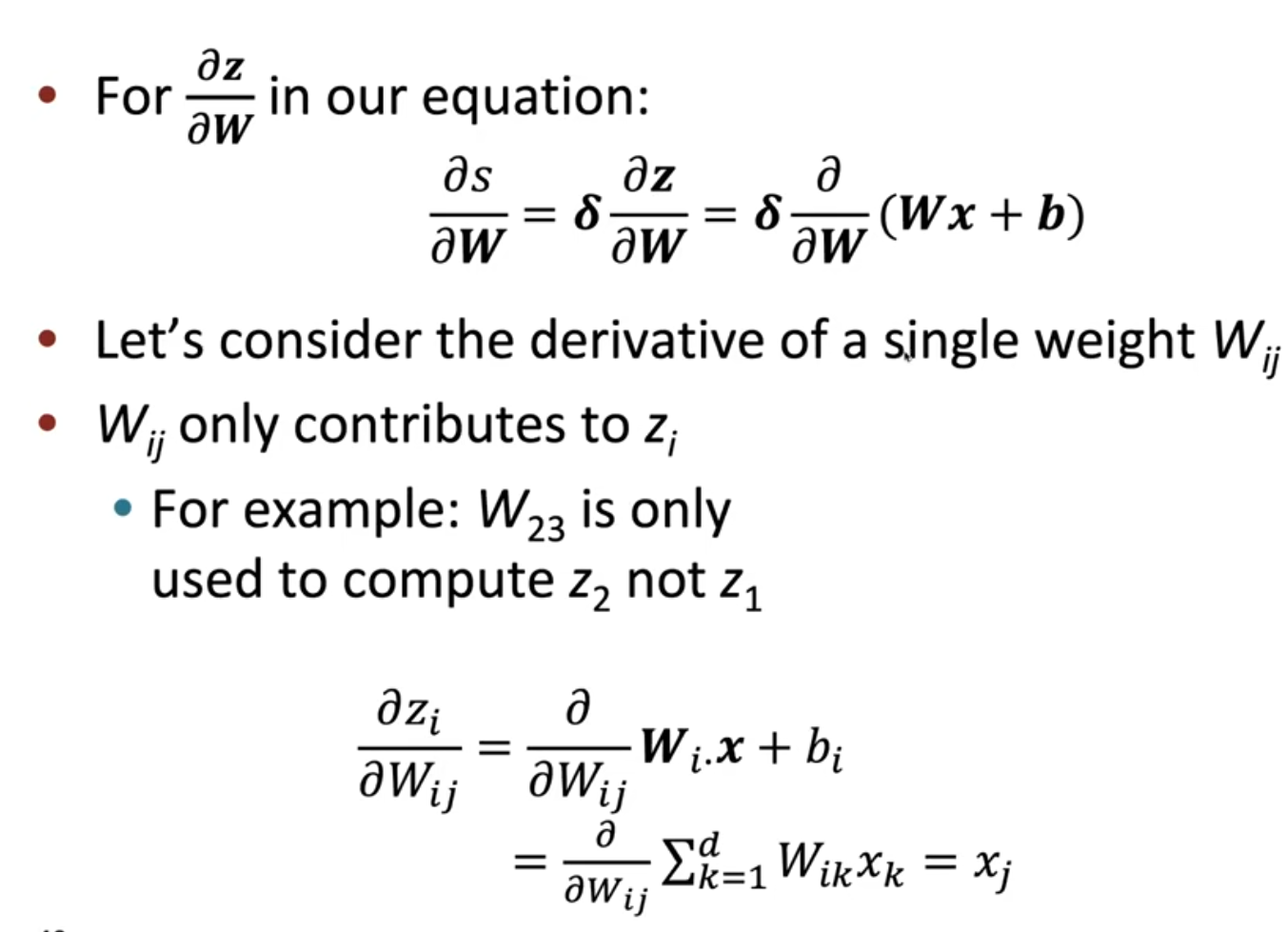
由于\(\frac{\partial{z}}{\partial{W}}∈\mathbb{R}^{n\times m\times n}\)，通过上面的计算我们可以想象出来这个立方体：俯视这个立方体，一共有\(n\)层，每一层都是一个\(m\times n\)的矩阵，第\(i\)层的矩阵的第\(i\)列为\(x\)，剩余元素都是\(0\)；那么\(\delta∈\mathbb{R}^{1\times n}\)，这两者怎么相乘呢？实际上，类比矩阵乘法，有\(\delta\frac{\partial{z}}{\partial{W}}∈\mathbb{R}^{1\times m\times n}\)（所以其实我们的答案最终是一个三维的张量）；具体来说，类比矩阵乘法，\(\delta_i\)与\(\frac{\partial{z}}{\partial{W}}\)的第\(i\)层矩阵相乘（这里广播一下），然后最终加起来（注意矩阵乘法在元素相乘之后也是加起来），就跟我们的答案一模一样了
那么上面是数学推导的过程，在代码中我们要求维度匹配（或至少能够广播），这就与我们的数学推导不一样，这时不要担心，我们就按照平常的推导方法，最后来调整梯度就好了
举一个计算图的例子

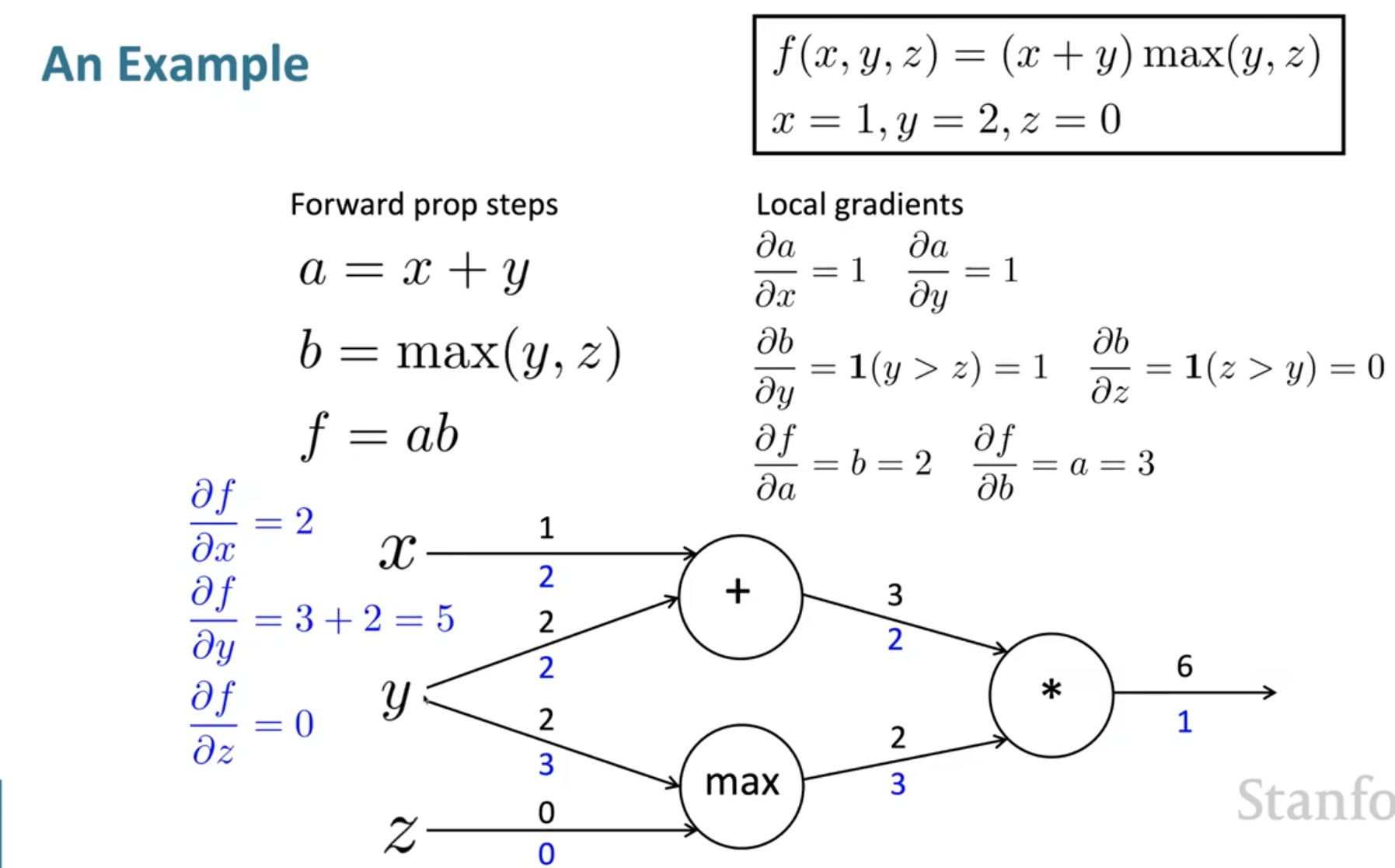
注意\(b\)也是一个二元函数，将\(\max\)符号打开就可以写出梯度了；最后的结果说明了\(x,y,z\)的微小改变量会对结果造成什么影响
提到了计算图，我们为什么要用计算图呢？这是为了节省计算开支。由于计算图是一个DAG，我们就可以存储中间变量（就像我们之前的推导令\(\delta\)一样），利用类似动态规划的过程计算梯度，而不是每计算一个梯度就要重头开始算起。对于一个节点，伪代码如下

我们现在一般都是用Pytorch，所以对检查梯度的需求比较小。但是有些时候如果我们想要自己实现一些层的话，我们可能会想写一写梯度检查的函数，这个时候我们的估计就要如下

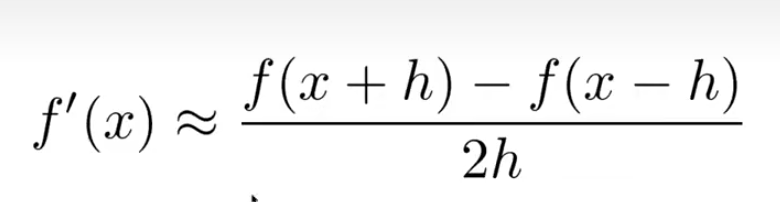
而不是使用我们高中的那种导数定义（单向的）。因为事实证明，双向的极限估计比单向的极限估计更加准确