14.1.3 跳元模型

跳元模型的似然函数选择为：

\[\prod_{t=1}^T \prod_{-m \leq j \leq m, \, j \neq 0} P(w^{(t+j)} \mid w^{(t)}) \]

而非其他形式，主要基于以下核心原因：

---

1. 模型目标的直接对应

跳元模型的核心目标是最大化给定中心词生成其上下文词的能力。

• 似然函数需直接反映这一目标：通过将每个中心词 $ w^{(t)} $ 生成其上下文窗口内所有词 $ w^{(t+j)} $ 的条件概率相乘，模型直接优化“中心词预测上下文词”的能力。
• 若使用其他形式（如预测中心词的概率乘积，类似CBOW），则与跳元模型的设计初衷不符。

---

2. 条件独立性假设的简化

跳元模型假设：给定中心词后，各上下文词的生成是相互独立的。

• 数学表达：
  \[P(\text{所有上下文词} \mid \text{中心词}) = \prod P(\text{单个上下文词} \mid \text{中心词}) \]

• 优势：
  • 将联合概率分解为独立项的乘积，极大简化计算复杂度。
  • 避免建模词序或上下文词之间的复杂依赖关系（如马尔可夫链），使模型更易训练。
• 代价：
  牺牲了部分语言结构信息（如词序相关性），但实践中通过大规模语料训练仍能捕捉有效语义。

---

3. 最大似然估计（MLE）的理论基础

• 似然函数的本质：在统计模型中，似然函数用于衡量参数（词向量）对观测数据（文本序列）的拟合程度。
• 选择乘积形式的原因：
  • 最大化所有中心词生成其上下文词的概率联合乘积，等价于最大化整个文本序列出现的概率。
  • 这符合最大似然估计的核心思想——找到使观测数据最可能的参数。

---

4. 对序列的全面覆盖

通过遍历所有时间步 $ t=1 $ 到 $ T $，并对每个时间步遍历其上下文窗口 $ j \in [-m, m] $，似然函数：

• 覆盖所有可能的中心词-上下文词对，确保每个词的上下文关系均被建模。
• 避免遗漏或重复：例如，词 $ w^{(t)} $ 作为中心词时，其上下文词为 $ w^{(t-2)}, w^{(t-1)}, w^{(t+1)}, w^{(t+2)} $（假设窗口大小为2）；而当 $ w^{(t+1)} $ 作为中心词时，其上下文词可能包括 $ w^{(t)} $。这种设计自然捕捉双向上下文关系。

---

5. 与参数化方式的一致性

跳元模型通过词向量点积 + softmax 定义条件概率：

\[P(w_o \mid w_c) = \frac{\exp(u_o^T v_c)}{\sum_{i \in V} \exp(u_i^T v_c)} \]

• 似然函数的形式需与参数化方式匹配：若使用其他形式的似然函数（如基于欧氏距离的概率），则无法直接利用词向量的点积特性，导致模型表达能力下降。
• 乘积形式与softmax的对数线性特性兼容，便于通过梯度下降优化。

---

6. 计算可行性与优化便利

• 对数转换：乘积形式的似然函数可通过取对数转换为求和形式：
  \[\log \mathcal{L} = \sum_{t=1}^T \sum_{-m \leq j \leq m, \, j \neq 0} \log P(w^{(t+j)} \mid w^{(t)}) \]
  避免数值下溢，同时保持优化目标的一致性。
• 负采样等近似方法：实际训练中，由于计算完整softmax代价高昂，可通过负采样近似优化目标，而乘积形式的似然函数天然支持这种近似。

---

7. 与其他模型的对比

• 对比CBOW模型：CBOW的似然函数是 $ \prod_{t} P(w^{(t)} \mid \text{上下文词}) $，即通过上下文预测中心词。跳元模型选择反向的生成方向，更擅长捕捉一词多义和低频词的关系。
• 若跳元模型采用类似CBOW的似然函数，则无法实现其设计目标（从中心词生成上下文），导致模型失效。

---

总结

跳元模型的似然函数形式是以下因素的综合结果：

1. 模型目标的直接映射（中心词 → 上下文词）；
2. 条件独立性假设的简化；
3. 最大似然估计的理论支撑；
4. 对序列的全面覆盖；
5. 与参数化方式的一致性；
6. 计算可行性的权衡。

这种形式在理论合理性与实践效率之间达到了平衡，使其成为跳元模型的最优选择。

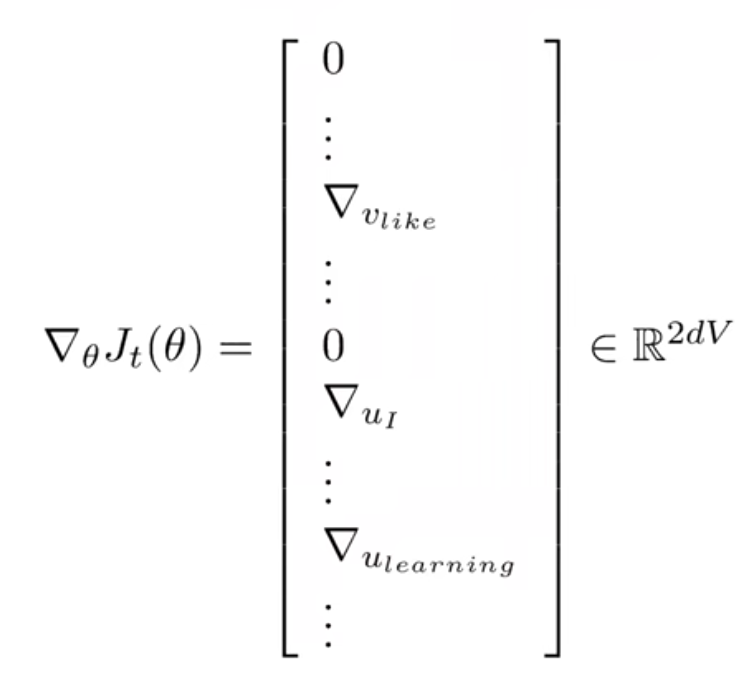
就像我们在这节最开始的批注一样，我们可以使用小批量梯度下降，但是为什么不用呢？这是因为我们最后得到的梯度非常稀疏。想一下，我们的词表非常大，所以我们小批量与词表相比就非常小了，设计到的词向量就很少，没有涉及到的词向量在梯度里面就会变成\(0\)，如下

为什么要用点积来衡量两个词之间的相似性呢？实际上，由于词向量的每一维代表着单词的某些信息，所以对于两个单词的词向量做点积，如果某一维的符号相同，那么会增大相似性，否则会减少相似性，这也比较符合直观；然后也可以想一下\(\text{Softmax}\)的意义，由于我们用点积衡量相似性，这个相似性就可能有正的也有负的，我们不想要负概率，所以我们取一个指数，在进行归一化，就得到了\(\text{Softmax}\).只不过这种方法也有些缺陷，比如我们可能会发现两个截然相反的词的词向量其实很相近，比如good和bad，happy和sad等等。这是因为文本库中经常出现两者的对立，比如有I am happy就有I am sad.我们单纯去捕捉上下文，捕捉出来的词向量当然是差不多的了

那么为什么我们不每个词只用一个向量来表示，而非要用两个向量（中心词向量和上下文词向量）来表示呢？这其实是为了更简单，如果只用一个向量来表示，求导的过程会出现一些问题，因为对于同一个词向量，他既可以当中心词向量也可以当上下文词向量，这样子求导的时候就会出现向量对自身的点积，会使得计算稍微复杂一点，没有什么其他的作用。实际上，我们最后训练出来的中心词向量和上下文词向量是非常相似的，这是因为每一个词都有既当中心词又当上下文词的机会，根据对称性可以得到上面的论断。但是下载下来的已经训练好了的词嵌入的每个单词的表示又只有一个，这是怎么回事呢？实际上，一般来说这个向量是中心词向量和上下文词向量平均的结果（不同的人有不同的平均方法）

word2vec实际上有一个缺陷，就是忽略了单词的位置