11.10.1 算法

Adam(Adaptive Moment Estimation)算法可以直观理解为“智能调整步长的动量法”，结合了动量加速和自适应学习率的优势。以下是逐步解释：

---

1. 核心思想：动量和自适应学习率的结合

• 动量（惯性）：类似滚下山坡的球，利用历史梯度方向保持运动惯性，减少震荡。
• 自适应学习率：根据每个参数的历史梯度幅度，自动调整步长。梯度大的参数步长小，梯度小的参数步长大。

---

2. 直观比喻：开车时的油门和刹车

• 动量（一阶矩）：踩油门的力度。如果连续下坡（梯度方向一致），逐渐加速（动量累积）；遇到颠簸（梯度方向变化），惯性会减缓急转弯。
• 自适应学习率（二阶矩）：根据路况调整刹车。遇到陡坡（梯度大），轻踩油门（步长减小）；平缓路面（梯度小），加大油门（步长保持或增大）。
• 偏差校正：启动时的“热车”过程。初始阶段车速表（动量估计）可能不准，校正后更真实。

---

3. 具体步骤分解

1. 计算梯度的一阶矩（动量）

   • 类似加权平均的历史梯度方向：
     ( m_t = \beta_1 \cdot m_{t-1} + (1-\beta_1) \cdot g_t )
     （(\beta_1)控制动量衰减率，如0.9）

2. 计算梯度的二阶矩（自适应学习率）

   • 类似历史梯度平方的加权平均：
     ( v_t = \beta_2 \cdot v_{t-1} + (1-\beta_2) \cdot g_t^2 )
     （(\beta_2)控制平方梯度衰减率，如0.999）

3. 偏差校正

   • 初始阶段（(t)较小时），(m_t)和(v_t)偏向零，需放大：
     ( \hat{m}_t = \frac{m_t}{1-\beta_1^t} ),
     ( \hat{v}_t = \frac{v_t}{1-\beta_2^t} )

4. 更新参数

   • 用校正后的动量方向和学习率调整步长：
     ( \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \cdot \hat{m}_t )
     （(\eta)是基础学习率，(\epsilon)防止除以零）

---

4. 直观效果

• 平坦区域（梯度小）：自适应学习率（(\sqrt{\hat{v}_t})小）放大步长，加速收敛。
• 陡峭区域（梯度大）：自适应学习率（(\sqrt{\hat{v}_t})大）缩小步长，避免震荡。
• 方向一致：动量累积加速，方向变化频繁时动量抑制震荡。

---

5. 对比其他算法

算法	特点
SGD	无动量，固定步长，易卡在局部最优点或震荡。
Momentum	有动量加速，但步长固定，对稀疏梯度效果差。
Adagrad	自适应步长，但累积梯度平方导致后期步长过小。
Adam	动量加速 + 自适应步长 + 偏差校正，适合大多数非凸优化问题，鲁棒性强。

---

总结

Adam像是一个智能驾驶员，既通过动量保持方向惯性，又根据路况（梯度大小）自动调节油门和刹车，最终高效平稳地抵达目的地（损失函数最小值）。

也就是说$\hat{v}$相当于动量法抑制某些方向上的震荡，$\frac{\eta }{\sqrt{{\hat{s}}_t}+ϵ}$相当于动态调整学习率

为什么要做式$(11.81)$的修正？事实上，如果我们将式$(11.80)$展开，就会发现下面这个式子

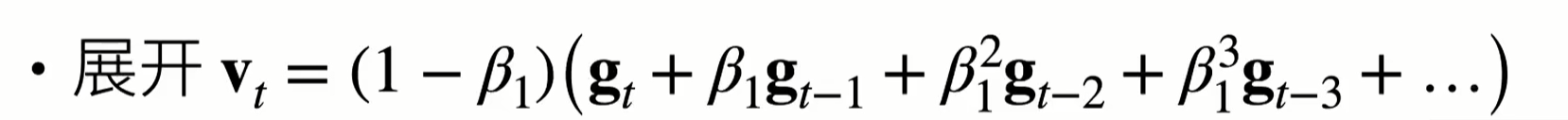
显然权重和是$1$。但是上面这个式子针对$t$比较大的情况，如果$t$比较小的话，根据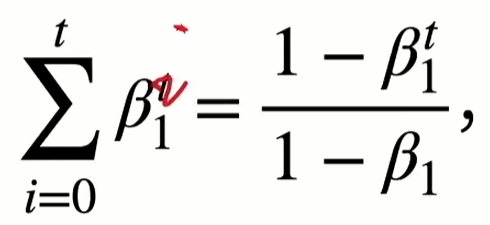
为了保证权重和仍然为$1$，所以要做这个修正

式$(11.82)$的一个直观理解：分子是让更新的方向比较平滑，分母是让每个维度的值都在合适的范围内（跟Normalization比较像）