数字序列

先将题目给出的\(b\)转化为单调不降序列。具体来说，对题目给出的原序列\(a\)，每个位置都减去其下标得到\(a^{'}\)；对任意一种构造的\(b\)，也都减去其下标得到\(b^{'}\)，显然\(\overset{n}{\underset{i=1}{\sum}}|a_i-b_i|=\overset{n}{\underset{i=1}{\sum}}|(a_i-)-(b_i-i)|=\overset{n}{\underset{i=1}{\sum}}|a^{'}_i-b^{'}_i|\)；下文都以\(a,b\)指代\(a^{'},b^{'}\)，并设\(c[i][j]\)表示\(a\)中的\(i\) ~ \(j\)排好序之后的数组（也就是说\(c\)是一个三维数组）

问题一：如果知道了对于\(a\)，最好的构造的\(b\)都是相同的（即\(b_1=b_2=...=b_n\)），那么\(b\)的值应该为什么？

答：显然为货仓选址问题，\(b\)取\(a\)的中位数（如果\(n\)为偶数，任取一个数都可以）

问题二：如果知道了对于\(a\)，存在一个下标\(k\)，使得\(1\) ~ \(k\)的最佳构造的\(b\)相同（i.e.当\(b_1=b_2=...=b_k\)时，\(\overset{k}{\underset{i=1}{\sum}}|a_i-b_i|\)最小）且\(k+1\) ~ \(n\)的最佳构造的\(b\)相同（i.e.当\(b_{k+1}=b_{k+2}=...=b_n\) 时，\(\overset{n}{\underset{i=k+1}{\sum}}|a_i-b_i|\)最小），是否可以构造出整个\(a\)的最佳构造，如果可以，如何构造？

答：可以构造出来。不妨设\(b_1=v_1,b_{k+1}=v_2\)

如果说\(v_1\leq v_2\)，那么整个\(a\)的最佳构造\(b\)就是\(b_1=b_2=...=b_k=v_1,b_{k+1}=...=b_n=v_2\)，这是因为\(\overset{n}{\underset{i=1}{\sum}}|a_i-b_i|=\overset{k}{\underset{i=1}{\sum}}|a_i-b_i|+\overset{n}{\underset{i=k+1}{\sum}}|a_i-b_i|\)，两者刚好取到下界且满足\(b\)单调不降

如果说\(v_1>v_2\)，考虑一个最优构造\(b\)，如果说\(b_k>v_1\)，我们将\(b\)的前\(k\)个数全部变成\(v_1\)，显然满足单调不降而且答案不会更差；否则的话，此时已经有\(b_k\leq v_1\)，如果此时还有\(b_{k+1}<v_2\)，我们将\(b_{k+1},b_{k+2},...,b_n\)全部改成\(v_2\)，显然满足单调不降且答案不会更差。也就是说一定存在一组最优解，使得\(b_k\leq v_1,b_{k+1}≥v_2\)。接下来考虑\(b\)的前\(k\)个数。假设\(b\)现在长成这个样子：

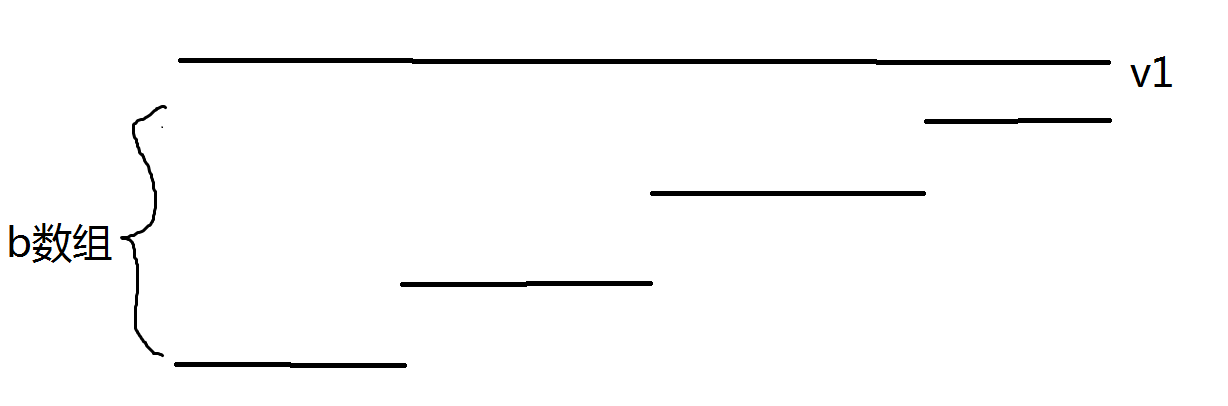
我们将除了最后一段\(b\)的剩下的\(b\)整体向上移动到倒数第二段\(b\)与最后一段\(b\)相同，如下

此过程答案一定不会更差。这是因为：设（移动前）最后一段\(b\)的下标为\(p+1\) ~ \(k\)，那么对于前\(p\)个数来说，\(c[1][p]_{\lfloor\frac{p}{2}\rfloor+1}\)（也就是\(a\)的前\(p\)个数的中位数，想一下为什么\(c\)的下标一定是\(\lfloor\frac{p}{2}\rfloor+1\)而不能是其他的）一定不会低于\(v_1\)（否则的话\(b\)的前\(p\)个数的取值不会是\(v_1\)，而是\(c[1][p]_{\lfloor\frac{p}{2}\rfloor+1}\)，这样答案肯定严格更优秀，就与我们的假设矛盾了），也就是说\(a\)的前\(p\)个数至少有\(\lfloor\frac{p}{2}\rfloor\)个数不低于\(v_1\)，而上面的移动让\(b\)的前\(p\)个数更加接近\(v_1\)，于是\(\overset{k}{\underset{i=1}{\sum}}|a_i-b_i|\)增加的值一定不会超过减少的值。推而广之，最后我们可以将\(b\)的前\(p\)个数变成相同的值，为\(b_k\)。此时我们不再考虑\(b_k\)后面的\(b\)，只考虑\(b\)的前\(k\)个数（也就是暂时先不管整个\(b\)的单调不降），将这\(k\)个数往\(v_1\)整体移动，显然答案也不会变差

对于\(b_k\)后面的\(b\)，我们也可以类似地证明，可以将所有的\(b\)都变成\(b_{k+1}\)并且可以再整体往\(v_2\)靠近；这样的话，我们就可以最终将\(b\)整体变成一样的值（注意最开始有\(b_k\leq b_{k+1}\)），并且答案不会更差

也就是说，对于整个\(a\)来说，存在一个最优解\(b\)使得所有\(b\)的值相同；由于当\(b\)全部取\(a\)的中位数的时候，是在满足“\(b\)的值都相同”的前提下，答案最小的解，所以这就是在满足“\(b\)的值都相同”的前提下的下界，而我们肯定可以达到这个下界，于是构造完毕

有了上面两个问题做铺垫，我们来考虑原问题。注意原问题是满足子问题最优性的。

假设现在已经构造好了前\(i\)个数的最优解，对于\(a_{i+1}\)，如果\(a_{i+1}≥b_i\)，那么\(b_{i+1}=a_{i+1}\)，从而找到了前\(i+1\)个数的最优解；否则的话，我们令\(b_i=b_{i+1}=\text{mid}\)，其中\(\text{mid}\)是\(a_i,a_{i+1}\)的中位数，这样的话就找到了在前\(i-1\)个\(b\)不变的情况下的最优解（因为此时根据子问题最优性，\(\overset{i-1}{\underset{j=1}{\sum}}|a_j-b_j|\)是最小的，而根据上面的问题的回答，\(\overset{i+1}{\underset{j=i}{\sum}}|a_j-b_j|\)也是最小的，两段同时取到了下界，于是为最优解）。然后考虑\(b_{i-1}\)，如果\(\text{mid}≥b_{i-1}\)，那么就停止循环，否则的话，令\(b_{i-1}=b_i=b_{i+1}=\text{Mid}\)（其中\(\text{Mid}\)为\(a_{i-1},a_i,a_{i+1}\)的中位数）。一直重复上述操作直到一个下标\(q\)（不能再继续操作了，因为已经构造了的后面一段的中位数不低于前面一段了），现在\(b\)的前\(q\)个数是我们之前已经构造好了的数，同时也是使得\(\overset{q}{\underset{j=1}{\sum}}|a_j-b_j|\)最小的构造（原问题满足子问题最优性），\(b_q\)后面的\(b\)的值都相同，为\(a_q\)后面的\(a\)的中位数，显然此时也有\(\overset{i+1}{\underset{j=q+1}{\sum}}|a_j-b_j|\)最小，于是原问题就取到了下界

但是上述过程一个\(b\)一个\(b\)地考虑太慢了，考虑优化。实际上，当我们循环到\(i+1\)的时候，\(b\)都是一段一段的，如下

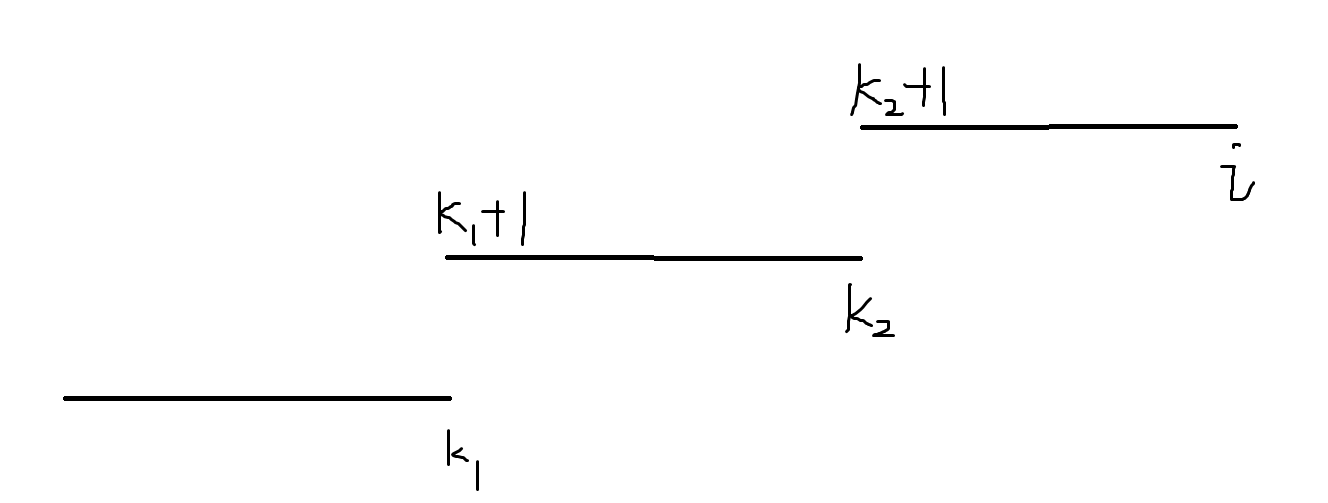
当我们加入\(a_{i+1}\)的时候直接与最后一段\(b\)进行比较，如果\(a_{i+1}<b_i\)，那么根据上面的第二个问题，可以直接找出\(k_2+1\) ~ \(i+1\)的最优解，此时如果\(a_{k_2+1}\) ~ \(a_{i+1}\)的中位数不低于前一段\(b\)（即\(k_1+1\) ~ \(k_2\)这一段），那么直接插入，否则根据问题二可以继续合并；直到某一时刻可以直接插入了就停止循环。此时一定是最优解，因为在插入位置的前面，有\(\sum|a_i-b_i|\)取到最小值，在插入位置的后面，有\(\sum|a_i-b_i|\)取到最小值，于是得到最优解

所以现在要解决的问题就是，如何快速得出两个数列合并之后的中位数。我们尝试用大根堆左偏树维护数列的前一半的数（如果数列有偶数个，那么堆顶为\(a_{\frac{n}{2}}\)，否则的话为\(a_{\frac{n+1}{2}}\)）。一个自然的想法就是在合并两个线段的时候，直接合并两个左偏树，得到的新的左偏树的堆顶就是新数列的中位数。但实际上这个样子是错误的，一个反例就是一个数列的数都非常小，另一个数列的数都非常大，于是新数列的中位数来源于比较小的数的数列，但是这个值却没有在其左偏树中维护，于是我们得不到新的中位数的信息。这就说明了左偏树不能直接维护没有任何限制的合并线段的中位数。然而，这道题目却可以这么做。因为：每次我们加入一个数\(a_{i+1}\)，假设\(a_{i+1}\)小于最后一段\(b\)的值，那么就说明\(a_{i+1}\)小于最后一段\(a\)的中位数，于是最后一段\(a\)加上\(a_{i+1}\)的中位数一定会在\(a_{i+1}\)和最后一段\(a\)前一半小的数中产生，就不会有上面的问题。归纳一下，假设我们已经正确合并了后面若干段\(a\)和\(a_{i+1}\)得到了正确的中位数。对于接下来的一段\(a\)，设这一段\(a\)的下标为\([l,r]\)，那么就是说我们已经得到了\([r+1,i+1]\)的中位数。由于\([r+1,i]\)的中位数不低于\([l,r]\)的中位数（这个尝试证明一下），加入了\(a_{i+1}\)后，最多让\([r+1,i]\)的中位数往前移动一位，分类讨论之后可以发现也不会存在上面所说的问题，可以直接用左偏树合并

时间复杂度是多少？每个线段会入队一次和出队一次。入队复杂度为\(O(1)\)，出队复杂度为\(O(\log n)\)

具体见打卡代码