异或

这道题目的思路比较好

由于\(1\)到\(n\)的路径很多，我们猜想，任意选一条路径可以通过某种异或运算来得到最优解

证明：假设我们选出的路径不是最优路径，那么对于另一条最优路径，一定可以通过我们选出的路径异或上若干个简单环来达到。举个例子说明

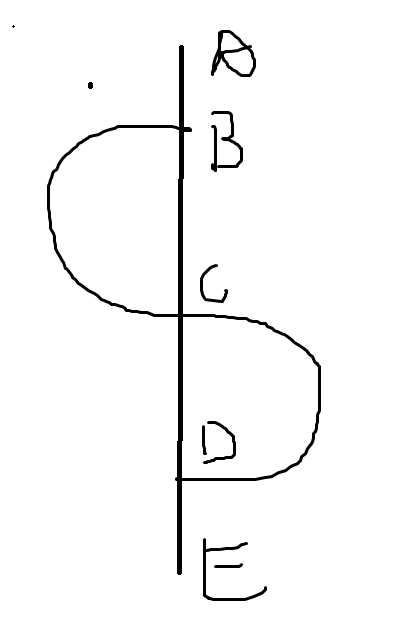
假设我们选出的是直线段\(AE\)，最优的路线是\(A\)先走直线到\(D\)，然后通过两个圆弧\(DCB\)到达\(B\)，最后再走直线到\(E\)，那么最优路线的值就等于我们选出的路径异或上图中的两个简单环

上述结论启发我们，找到图中所有的简单环，然后用我们选出来的路径加上若干个简单环能够到达的最大值就是答案

但是我们任选简单环，是否一定能够找到一条路径对应呢？答案是肯定的，对于任意一个简单环，我们先从\(1\)走到环上的某一点\(x\)，然后走一遍这个环到\(x\)，再从\(x\)又回到\(1\)号点就相当于得到了这个环的异或值

于是我们找出所有简单环考虑线性基

当我们化出行简化梯形矩阵的时候，记住每个非零行是若干个\(a\)的异或，也就是说我们任取非零行来异或一定可以在原来的\(a\)中找到一些\(a\)来异或起来对应；而这些非零行又是极大线性无关组，显然可以覆盖问题空间

注意行简化梯形矩阵有“异或运算”这道题目所说的性质，所以我们依次从高位到低位贪心即可

找出所有简单环的代码要记住，另外有个结论：简单环的个数与边数同级

update 2024.8.7

重新做这道题目想到了更加严谨的证明

遇事不决直接缩点。对原图缩点成e-DCC，于是图就长成了这个样子

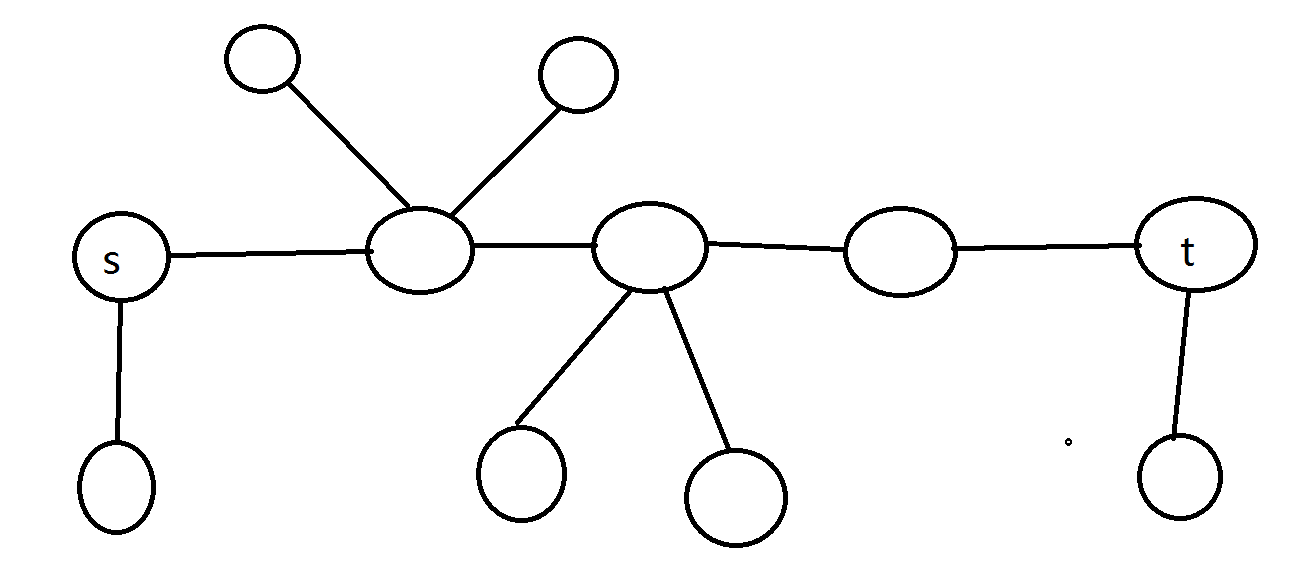
其中\(1\)号点属于\(s\)这个缩点，\(n\)号点属于\(t\)这个缩点

不难知道，对于任意一种路径，\(s\)到\(t\)上的非e-DCC边会且只会被经过一次，其余非e-DCC的边一定不会产生贡献（要么压根就不经过，要么经过的时候由于回溯导致经过了偶数次贡献抵消），所以我们现在来考虑e-DCC里面的边

先来考虑不在\(s\)到\(t\)的路径上的e-DCC中的e-DCC边。我们从一个e-DCC到另一个e-DCC，假设是从原图的\(p\)号点到\(q\)号点（设这个时刻为\(T_1\)），那么回溯的时候，我们一定会从\(q\)走到\(p\)，而当我们准备从\(q\)走到\(p\)的时候（设这个时刻为\(T_2\)），时刻\(T_1\)到时刻\(T_2\)，我们的路径一定由若干个简单环组成（原因：假设我们从\(T_1\)到\(T_2\)经过的点为\(q,q_1,q_2,...,q_n,q\)，因为图是有限的，所以在不重复经过点的情况下最终一定无法回溯，于是肯定会走出一个简单环，假设有\(q_i=q_j\)且这中间就是一个简单环，我们将路径删除这些点，然后问题规模就缩小了，由于起点终点都是\(q\)，于是我们最终可以将路径拆分成若干个简单环）；这就是说，对于任意一条路径，其属于不在\(s\)到\(t\)的路径上的e-DCC中的e-DCC边，都可以看成是某个简单环的贡献，于是我们可以将路径简化为只考虑经过在\(s\)到\(t\)的路径上的e-DCC中的e-DCC边

假设我们随便找了一条从\(1\)到\(n\)的路径（只经过在\(s\)到\(t\)的路径上的e-DCC中的e-DCC边），而最优路径不是这一条，我们可以假设最优路径没有简单环（否则仍然可以拆分），于是他们两个就长成下面这个样子

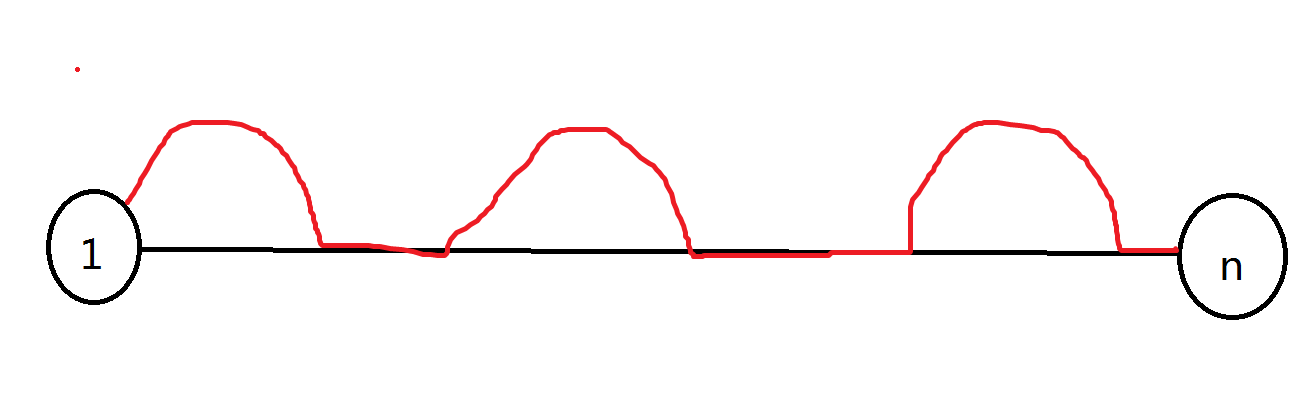
其中黑色是我们找的路径，红色是最优路径，而显然红色路径可以看成是黑色路径加上若干个简单环，于是得证

然后找简单环的代码像无向图tarjan搜索树那样理解就很好理解了，而且不难证明结论：简单环的个数与边数同级（因为只有一条回溯边才可以产生一个简单环）