搜索算法合集 - By DijkstraPhoenix
搜索算法合集
By DijkstraPhoenix
深度优先搜索 (DFS)
引入
如果现在有一个迷宫,如何走路径最短?
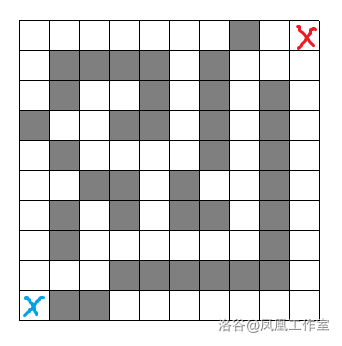
方法
走迷宫最简单粗暴的方法式什么呢?当然是把所有路都走一遍!
电脑具有强大的算力,这种暴力的事情当然是交给电脑做。
深搜的本质:一条路走到底,走到死胡同再往回走,回到上一个岔口继续走,直到找到正确的路
实际上,任何一条路都可以看做是一个只有一个岔口的分岔路,所以不需要把路和岔口分开计算。
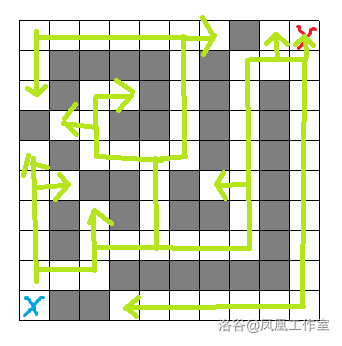
概念:从死胡同返回的步骤叫做回溯
由于深搜不能保证第一次找到的路径为最短路径,所以需要统计所有路线
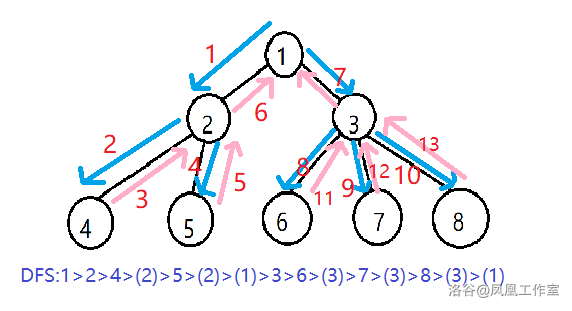
如果我们把迷宫里的路径抽象为一张图(树),那么就像上图一样。箭头表示路径,粉色和括号里的是回溯
深搜一般使用递归实现,走过的每个位置都要打上标记,同一条路不能再走一遍
四联通和八连通:
有些走迷宫题目是四联通的(即上下左右),也有些是八连通的(即上、下、左、右、左上、左下、右上、右下),需要仔细观察题目要求
四联通位移数组:dx[]={1,0,-1,0}; dy[]={0,1,0,-1};
八连通位移数组:dx[]={1,0,-1,0,1,1,-1,-1}; dy[]={0,1,0,-1,1,-1,1,-1};
主算法代码:
int maze[MAXN][MAXN];//存储迷宫 0表示当前节点可以走,1表示不能走
bool vis[MAXN][MAXN];//打标记
const int dx[]={1,0,-1,0};
const int dy[]={0,1,0,-1};//位移数组,分别对应 上右下左(如果是八向移动的话要改成对应的)
int n,m,stx,sty,edx,edy;//地图长宽以及起点和终点的坐标
int ans=0x7f7f7f7f;//最短距离,要初始化为极大值
void dfs(int x,int y,int z)//x和y是当前位置的坐标,z是走过的步数
{
if(x==edx&&y==edy)//到了终点
{
ans=min(ans,z);//更新答案(如果答案还是极大值,说明无法到达终点)
return;
}
vis[x][y]=true;//打标记
for(int i=0;i<4;i++)//枚举四个方向
{
int nx=x+dx[i],ny=y+dy[i];//下一个应该走到的位置
if(nx<1||nx>n||ny<1||ny>m)continue;//不能走出地图(这个要写在灵魂拷问的最前面,否则访问数组要越界)
if(maze[nx][ny]==1)continue;//不能卡墙里
if(vis[nx][ny])continue;//不能走你走过的路
dfs(nx,ny,z+1);//走到下一个节点
}
vis[x][y]=false;//重点!回溯时要清除标记!
}
例题
连通块问题
求1的连通块数量
这是一类重要的题目!
本题可以使用 DFS 从每一个点开始将每一个连通块都标记并计数
上图就是标记出的连通块
我们可以从连通块的任意一个位置开始,遍历整个连通块,并把这个连通块的所有点打上标记(防止重复计算)
这个方法也叫洪水填充法(Flood Fill)
强烈建议在网上找几篇专门讲连通块的博客学一下
#include<bits/stdc++.h>
using namespace std;
int maze[105][105];
bool vis[105][105];
int n,m,ans;
void dfs(int x,int y)
{
vis[x][y]=true;
for(int i=0;i<4;i++)
{
int nx=x+dx[i],ny=y+dy[i];
if(nx<1||nx>n||ny<1||ny>m)continue;
if(maze[nx][ny]!=1)continue;
if(vis[nx][ny])continue;
dfs(nx,ny);
}
//注意!!!此处不要回溯(标记是给后面的连通块看的)
}
int main(void)
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
cin>>maze[i];
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(!vis[i][j]&&maze[i][j]==1)//如果这个点没找过并且是连通块的一部分,那么就是一个新的连通块
{
ans++;
dfs(i,j);//为整个连通块打上标记
}
}
}
cout<<ans;
return 0;
}
八皇后问题
本题的每一步都决定一个皇后的位置,由输出格式就可以看出,我们可以按每一列的顺序计算。一个皇后会独占一行、一列、两斜线,因为是按列计算的,不需要给列打标记,则需要 3 个标记数组。
(其实可以看一下洛谷上的题解)
#include<bits/stdc++.h>
using namespace std;
bool vis[15],vis1[35],vis2[35];
int n;
int nod[15];
int sum=0;
void dfs(int k)
{
if(k>n)
{
sum++;
if(sum<=3)//前3个要输出方案
{
for(int i=1;i<=n;i++)cout<<nod[i]<<" ";
cout<<endl;
}
return;
}
for(int i=1;i<=n;i++)
{
if(vis[i])continue;
if(vis1[i+k-1])continue;
if(vis2[i-k+13])continue;
vis[i]=true;
vis1[i+k-1]=true;
vis2[i-k+13]=true;//可以手动模拟一下行列坐标和斜坐标的关系,加13是防止计算出负数
nod[k]=i;//保存方案
dfs(k+1);
vis[i]=false;
vis1[i+k-1]=false;
vis2[i-k+13]=false;
}
}
int main(void)
{
cin>>n;
dfs(1);
cout<<sum;
return 0;
}
全排列问题
这是一个重要的题目!
按照题意模拟搜索即可
#include<iostream>
#include<cstdio>
using namespace std;
int n,a[1000],vis[1000];
void dfs(int step)
{
if(step==n+1)
{
for(int i=1;i<=n;i++)
{
printf("%5d",a[i]);//题目要求格式化输出
}
cout<<endl;
}
for(int i=1;i<=n;i++)
{
if(vis[i]==1)continue;
a[step]=i;
vis[i]=1;
dfs(step+1);
vis[i]=0;
}
}
int main(void)
{
cin>>n;
dfs(1);
return 0;
}
一些建议练习的题
求细胞数量
提示:联通块问题,不要清除标记,从每个未标记且是细胞的块出发,将整个块打上标记
广度优先搜索 (BFS)
引入
还是刚才的迷宫问题

方法
除了把每一条路走一遍,其实还可以从起点倒水。这样可以根据水流找到路径。
BFS 模拟洪水往外扩散的样子,按层遍历。
这样做有一个好处:如果像迷宫这样,每两个相邻的方块之间的距离都一样的话,第一次找到的路径就是最短路径(每一层走过的路程都一样),如果没有这个条件就不保证最短
以下是 BFS 和 DFS 策略上的对比:
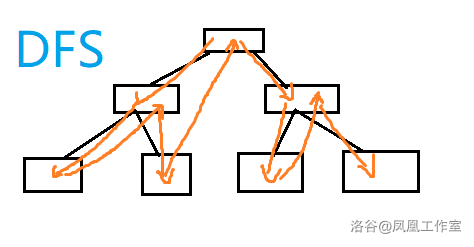
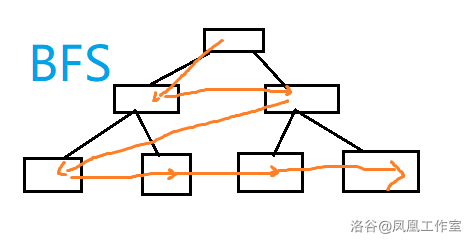
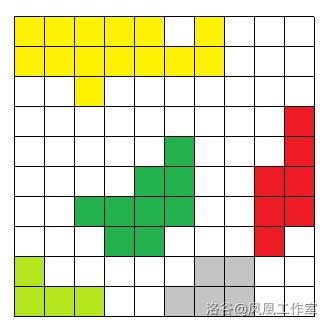
放到迷宫里就是这个样子:
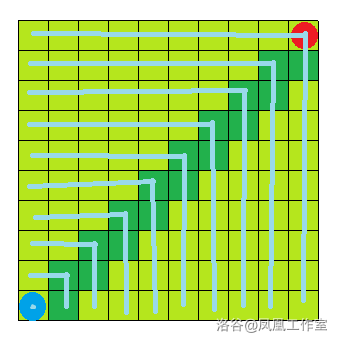
(图中深绿色代表路径,浅绿色代表访问过的点,线表示遍历的每一层)
重点!因为同一层的兄弟节点无法直接像 DFS 那样转移,所以会把应该访问的节点放到一个队列里,挨个处理
主要代码:
struct node
{
int x,y,step;//节点坐标和已经走过的步数
};
queue<node>Q; //队列
bool vis[MAXN][MAXN];//标记数组
int maze[MAXN][MAXN];//存储地图,0可以走,1不能走
int stx,sty,edx,edy;
const int dx[]={1,0,-1,0};
const int dy[]={0,1,0,-1};
int n,m;//地图长宽
void bfs(void)//bfs其实不需要封装在函数里,它不需要递归
{
Q.push(node{stx,sty,0});
vis[stx][sty]=true;//初始状态
while(!Q.empty())//直到所有的状态都处理完毕
{
int x=Q.front().x,y=Q.front().y,st=Q.front().step;//取出队首元素
Q.pop();//很重要!不要忘了出队列
for(int i=0;i<4;i++)
{
int nx=x+dx[i],ny=y+dy[i];
if(nx<1||nx>n||ny<1||ny>m)continue;
if(vis[nx][ny])continue;
if(maze[nx][ny]==1)continue;//灵魂三问
Q.push(node{nx,ny,st+1});//加入处理队列
vis[nx][ny]=true;//打标记 注意!BFS没有回溯!
if(nx==edx&&ny==edy)//到终点了
{
cout<<st+1;
exit(0);//封装在cstdlib库里,直接退出整个程序
}
}
}
}
例题
Catch That Cow S
本题的转移有三种:前进1步,后退1步,乘2
其实本题代码很简单(别看有点长)实际上是三个转移
#include<bits/stdc++.h>
using namespace std;
int t,x,y;
bool vis[100005];
queue<int>Q,step;
int main(void)
{
cin>>t;
for(int test(1);test<=t;test++)
{
cin>>x>>y;
Q.push(x); //入队
step.push(0); //初始他一步也没走,step入队0
vis[x]=true; //标记
while(!Q.empty()) //step和Q是同步的,不需要额外判断
{
//取队首元素
int s=Q.front();
int st=step.front();
Q.pop(); //出队
step.pop();
int nst=st+1;
int ns;
//找可以的情况
ns=s+1;//前进1步
if(ns>=1&&ns<=100000&&vis[ns]!=true) //条件成立
{
vis[ns]=true; //标记
Q.push(ns); //入队
step.push(nst);
if(ns==y) //找到了
{
//因为BFS第一个找到的一定是最短的路径,直接输出
cout<<nst;
break;
}
}
ns=s-1;//后退1步
if(ns>=1&&ns<=100000&&vis[ns]!=true) //条件成立
{
vis[ns]=true; //标记
Q.push(ns); //入队
step.push(nst);
if(ns==y) //找到了
{
//因为BFS第一个找到的一定是最短的路径,直接输出
cout<<nst;
break;
}
}
ns=s*2;//乘2
if(ns>=1&&ns<=100000&&vis[ns]!=true) //条件成立
{
vis[ns]=true; //标记
Q.push(ns); //入队
step.push(nst);
if(ns==y) //找到了
{
//因为BFS第一个找到的一定是最短的路径,直接输出
cout<<nst;
break;
}
}
}
}
}
字串变换
本题需要寻找可以变换的部分进行转移。字符串长度不长,可以暴力配对
#include<bits/stdc++.h>
using namespace std;
#define int long long
string ap[25],bp[25];
int le;
queue<string>q;
queue<int>step;//本代码没有使用结构体而是使用两个队列
map<string,bool>vis;
signed main(void)
{
string a,b;
string ia,ib;
cin>>a>>b;
while(cin>>ia)
{
cin>>ib;
ap[++le]=ia;
bp[le]=ib;
}
q.push(a);
step.push(0);
vis[a]=true;
while(!q.empty())
{
string s=q.front();q.pop();
int st=step.front();step.pop();
if(st==10)continue;
for(int i=1;i<=le;i++)
{
int start=0;
while(true)
{
int fd=s.find(ap[i],start);//寻找匹配字符串
if(fd==string::npos)break;
start=fd+1;
string tmp=s.substr(0,fd);
tmp+=bp[i];
tmp+=s.substr(fd+ap[i].length());
if(vis[tmp])continue;
q.push(tmp);//转移
step.push(st+1);
if(tmp==b)//找到了
{
cout<<st+1;
return 0;
}
}
}
}
cout<<"NO ANSWER!";
return 0;
}
一些建议的题
迭代加深搜索 (IDDFS 或 IDS)
引入
众所周知所有的搜索算法都是 DFS 或 BFS 的变形,迭代加深搜索是 DFS 的一种变形,它在进行深搜时限定了搜索深度
这看起来是没事找事,对吧?
如果我们遇到了一道搜索题每一层的宽度无限但深度有限,可以用 DFS 解决;如果深度无限宽度有限,可以使用 BFS。那么深度和宽度都是无限的呢?
于是就有了迭代加深搜索
思想
迭代加深搜索限定搜索深度其实就是将无限的深度转化为有限的深度
迭代加深搜索的核心就在于进行多次搜索,每次搜索依次放宽深度限定,这样第一次找到的必定是步数最少的解(这里的步数指搜索的层数而非贡献值总和)
就像这样:
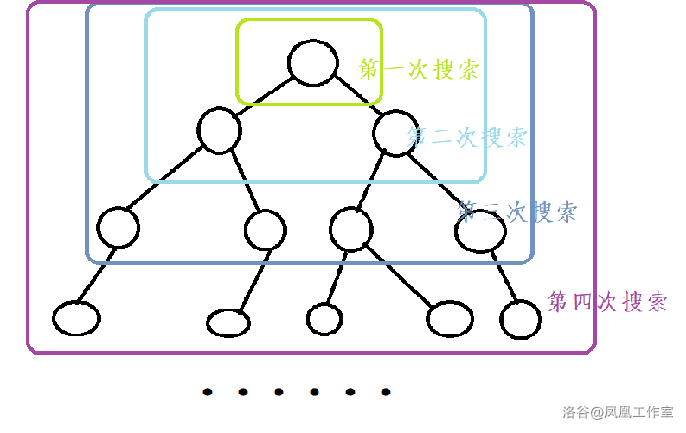
核心代码如下:
int lmt;//深度限制
bool flg;//是否成功
void dfs(int dep/*深度*/,/*一些别的东西*/)
{
if(dep>lmt)return;//超过限制直接返回
if(/*找到了*/)
{
flg=true;
return;
}
/*干一些事*/
}
int main(void)
{
/*输入以及初始化*/
for(lmt=1;lmt<=20/*最大深度,一般在20左右,具体按题意来看*/;lmt++)//循环进行多次搜索
{
dfs(1,/*一些别的参数*/);
if(flg)//成功了
{
/*输出答案*/
}
}
/*没找到的情况*/
return 0;
}
例题
埃及分数
解法
这道题很明显搜索深度和宽度都是无限的(题目中的限制每个分数不小于1/1e7,但由于数量巨大,无法直接计算,近似看做无限),需要迭代加深搜索求解
每次搜索限制分数的个数,本题一定有解,所以可以无限循环减少限制
这种算法无法通过 HACK 数据,满分解法会在后续章节中讲解
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int deep=1;//深度限制
bool flag=false;
int tmp[15],ans[15];
int gcd(int x,int y)
{
if(y==0)return x;
return gcd(y,x%y);
}
void dfs(int k,int a,int b)
{
if(k>deep)//超过最大深度
return;
if(a==1&&b>tmp[k-1])//更优解
{
tmp[k]=b;
if(!flag||tmp[k]<ans[k])
{
for(int i=1;i<=deep;i++)
ans[i]=tmp[i];
}
flag=true;
return;
}
int l=max(b/a,tmp[k-1]+1);
int r=(deep-k+1)*b/a;
if(flag&&r>=ans[deep])
r=ans[deep]-1;
for(int i=l;i<r;i++)
{
tmp[k]=i;
int gc=gcd(a*i-b,b*i);
dfs(k+1,(a*i-b)/gc,b*i/gc);
}
}
signed main(void)
{
int a,b;
cin>>a>>b;
int gc=gcd(a,b);
a/=gc;
b/=gc;//化简(这一步好像不需要,最好加上)
tmp[0]=1;
for(deep=1;;deep++)
{
dfs(1,a,b);
if(flag)//找到答案
{
for(int i=1;i<=deep;i++)
{
cout<<ans[i]<<" ";
}
break;
}
}
return 0;
}
一些建议的题
启发式搜索 (A*)
引入
对于一个有很多条可行的路径的迷宫,如何能够最快速地找到最短路径?
虽然对于搜索,他的本质是暴力,也就是把所有的路径走一遍,但是,这不代表搜索不能变得智能。
那么能不能让搜索算法每次寻找最优的路径呢?
接下来介绍启发式搜索,这是一种相对智能的搜索算法。
原理
启发式搜索 (A*) 是一种的 BFS 的改良,它拥有一个估价函数 \(f(x)=g(x)+h(x)\),其中 \(g(x)\) 是已走的步数,\(h(x)\) 是预计还有多少步到达终点(在某些题目中,估价函数不一定只真实的最短路,但一定要保证快到达终点的状态在离终点远的状态之前),\(f(x)\) 为估计从起点到终点的步数。
这样,A* 每次都找最有可能成为最优解的一步,用优先队列维护。
那么此时维护的就是全局最优解,所以启发式搜索第一次找到的一定是最优解,第 \(k\) 次找到的一定是第 \(k\) 优解。(注意:有些题目要求的是严格第 k 解,即对于每个 P ∈ [1,k) , 第 P 解 ≠ 第 P+1 解)
以下是 A* 和 BFS 在没有障碍的地图中寻路的对比(深绿是最终路径,浅绿是访问过的节点)
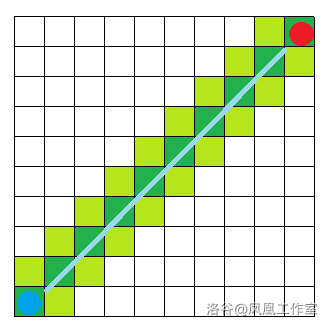

可以发现 A* 比 BFS 访问的这些无用节点少了很多。
例题
八数码
这道题由于状态太多使用朴素的 BFS 明显过不了,可以考虑 A*。(本题还有双向搜索的解法,会在后面的章节内讲解)
这里我们的 \(h(x)\) 定义为当前状态和目标状态中,不同的数码个数,那么首次到达即为最优解。
本题可以使用康托展开将矩阵转化为一个整数(相当于哈希),这里的代码不考虑。代码使用结构体 + set 存储。
#include <bits/stdc++.h>
using namespace std;
const int dx[] = {1, -1, 0, 0};
const int dy[] = {0, 0, 1, -1};
struct ary //存储状态
{
int s[5][5];
bool operator<(ary x) const
{
for (int i = 1; i <= 3; i++)
{
for (int j = 1; j <= 3; j++)
{
if (s[i][j] != x.s[i][j])
return s[i][j] < x.s[i][j];
}
}
return false;
}
} inp, ed;
int h(ary x)//h()函数
{
int sum = 0;
for (int i = 1; i <= 3; i++)
{
for (int j = 1; j <= 3; j++)
{
if(x.s[i][j]!=ed.s[i][j])sum++;
}
}
return sum;
}
struct node //这个结构体是用于自定义优先队列的判断的
{
ary ar;
int t;
bool operator<(node x) const
{
return h(ar) + t > h(x.ar) + x.t;
}
};
string sed = "123804765";
priority_queue<node> heap;
set<ary> vis;
int main(void)
{
for (int i = 1; i <= 3; i++)
{
for (int j = 1; j <= 3; j++)
{
ed.s[i][j] = sed[(i - 1) * 3 + j - 1] - '0';
char s;
cin >> s;
inp.s[i][j] = s - '0';
}
}
heap.push((node){inp, 0});
while (!heap.empty())//A*算法主体(其实就是优先队列优化BFS)
{
node fa = heap.top();
heap.pop();
if (!h(fa.ar))//首次找到即为最优解
{
cout << fa.t;
return 0;
}
int sx, sy;
for (int i = 1; i <= 3; i++)
{
for (int j = 1; j <= 3; j++)
{
if (fa.ar.s[i][j] == 0)
{
sx = i;
sy = j;
}
}
}
for (int i = 0; i < 4; i++)
{
int nx = sx + dx[i];
int ny = sy + dy[i];
if (1<=nx&&nx<=3&&1<=ny&&ny<=3)//移动数码
{
swap(fa.ar.s[sx][sy], fa.ar.s[nx][ny]);
if (!vis.count(fa.ar))
{
vis.insert(fa.ar);
heap.push((node){fa.ar, fa.t + 1});
}
swap(fa.ar.s[sx][sy], fa.ar.s[nx][ny]);
}
}
}
return 0;
}
一些建议的题
K短路
提示:可以用最短路算法预处理 \(h(x)\),P2483 使用 A* 无法得到满分(可以拿部分分)
启发式迭代加深搜索 (IDA*)
原理
在前面几章提到过迭代加深搜索对搜索深度的限制,和启发式搜索通过估价函数和优先队列优化 BFS
那么就可以将两者结合起来,通过估价函数限制搜索深度,即保证 \(g(x) + h(x) \leq C\)
利用这个性质进行剪枝可以大幅减少递归的层数,从而降低时间复杂度
IDA* 利用 DFS 进行搜索,这样利于剪枝
优点 & 缺点
由于 IDA* 是 A* 和 IDS 的结合体,它拥有两者的优点和缺点
优点
-
无需打标记和排序,利于深度剪枝
-
空间需求少
缺点
与 IDS 相同,IDA* 每次搜索时会重复搜索以前的结点
实现
伪代码:
int lmt;//深度限制
bool flg;//是否成功
void dfs(int dep/*深度*/,/*一些别的东西*/)
{
int h;
/*一些用于计算估价函数的过程*/
if(dep+h>lmt)return;//超过限制直接返回
if(/*找到了*/)
{
flg=true;
return;
}
/*干一些事*/
}
int main(void)
{
/*输入以及初始化*/
for(lmt=1;lmt<=20/*最大深度,一般在20左右,具体按题意来看*/;lmt++)//循环进行多次搜索
{
dfs(1,/*一些别的参数*/);
if(flg)//成功了
{
/*输出答案*/
}
}
/*没找到的情况*/
return 0;
}
例题
埃及分数
(又是这道题)
解法
对于之前的代码会被 HACK 数据卡成 TLE,所以需要通过启发式进行剪枝,从而优化时间复杂度
定义 \(h(x) = 剩下分解还需要的最少的分数数量\)
计算 h(x) 的步骤可以通过贪心实现,即每次都将当前分数 \(\frac {a}{b}\) 减去一个最大的 \(\frac {1}{x} , \frac {1}{x} \leq \frac {a}{b}\)
可以证明这样一定能存在一个解,并且一定步数最少
代码
忘了二分怎么写了,懒得写完整代码了,根据提示和模板自己写吧
一些建议的题
双向搜索
引入
先来计算一下 \(4^8\) 和 \(2 × 4^4\) 的值
不难发现,\(4^8 = 65536\),
\(2 × 4^4 = 512\)
也就是说,底数不变,在指数层级上减半时,这个数会大幅缩小
搜索作为一个指数层级的时间复杂度的算法来说亦是如此。所以要优化搜索,可以考虑将指数(也就是搜索的层数)减半
于是双向搜索就诞生了
原理
双向搜索,顾名思义就是从起点和终点同时出发,两者相遇时就找到了答案
为了判断两者相遇,可以给走过的点打上标记。为了防止从起点出发的两条路径相遇(或者从终点出发),一般把标记改为染色,即给不同起点的路径打上不同的标记,可以理解为将 vis 数组改成了 color 数组
双向搜索可以应用于大多数搜索算法,这里只介绍双向 BFS 和双向迭代加深
双向 BFS
双向 BFS 有两种写法,一种是建两个队列,分别存储从起点开始的点和从终点开始的
每次循环先后取出两个队列的点进行拓展
伪代码如下:
queue<pair<int,int> >q1,q2;//q1从起点出发,q2从终点出发,pair存储位置和步数
int col[10005];//染色,1从起点出发,2从终点出发
int st,ed;//起点和终点
void Double_BFS(void)
{
col[st]=1;
col[ed]=2;
q1.push(make_pair(st,0));
q2.push(make_pair(ed,0));//初始状态
while((!q1.empty())||(!q2.empty()))//只要其中一个还能走就继续拓展
{
//从起点出发的
int x=q1.front().first;
int step=q1.front().second;
q1.pop();
for(/*一些分支*/)
{
int nx;
/*计算新的点*/;
q1.push(make_pair(nx,step+1));//新的状态入队
if(col[nx]==2)//找到了
{
cout<<step+1;
return 0;
}
col[nx]=1;//打上颜色
}
//从终点出发的
x=q2.front().first;
step=q2.front().second;
q2.pop();
for(/*一些分支*/)
{
int nx;
/*计算新的点*/;
q2.push(make_pair(nx,step+1));//新的状态入队
if(col[nx]==1)//找到了
{
cout<<step+1;
return;
}
col[nx]=2;//打上颜色
}
}
cout<<"Not found!";//没找到
return;
}
另一种写法是将起点和终点的放在一个队列里
伪代码如下:
struct node
{
int step,x,color;//步数,位置和颜色
};
queue<node>q;
int col[10005];//染色,1从起点出发,2从终点出发
int st,ed;//起点和终点
void Double_BFS(void)
{
col[st]=1;
col[ed]=2;
q.push(node{0,st,1});
q.push(node{0,ed,2});//初始状态
while(!q.empty())//只要其中一个还能走就继续拓展
{
//从起点出发的
int x=q.front().x;
int step=q.front().step;
int color=q.front().color;
q.pop();
for(/*一些分支*/)
{
int nx;
/*计算新的点*/;
q1.push(node{step+1,nx,color});//新的状态入队
if(col[nx]==3-color)//找到了
{
cout<<step+1;
return 0;
}
col[nx]=color;//打上颜色
}
}
cout<<"Not found!";//没找到
return;
}
注:之前的八数码也可以通过双向 BFS 实现
双向迭代加深
原理同上
伪代码如下:
int deep;//最大深度
bool found;//是否找到
int Color[10005];//颜色数组
void dfs(int x,int d,int col)//位置,深度和颜色
{
if (Color[x]+col==3)
found=true;
Color[x]=dir;
if(d==deep)
return;
for(/*遍历可以达到的状态*/)
{
int nx;
/*计算nx*/
dfs(nx,d+1,col);
}
//无需回溯
}
void Solve(void)
{
while(deep<=MaxDeep/2)
{
dfs(st,0,1);
if (found)
//找到的情况
//最大深度为奇数时这里要特判
dfs(ed,0,2);
if (found)
//找到的情况
deep++;//加深深度
}
}
B* 搜索算法
没错,就是 B*,但和 A* 关系不大
B* 是一种寻路算法,属于仿生算法,它模仿动物寻路的算法
路径规划
计算机寻路的方式是将所有路径都走一遍,但是动物不可能花这么多时间寻路
动物寻路会朝着目标点走(而不是漫无目的地瞎走)
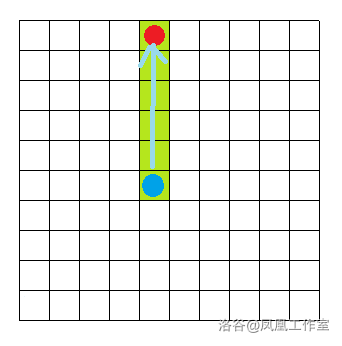
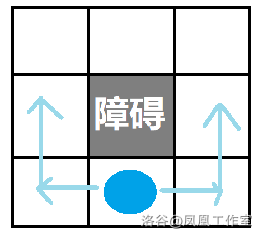
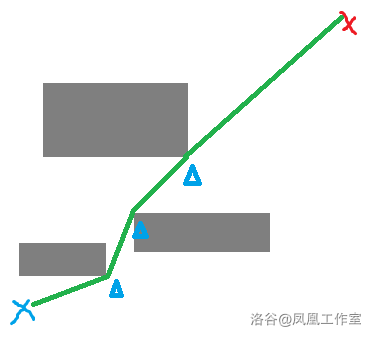
这里我们考虑四联通,如果目标在当前位置的正东/西/南/北方时会直接朝那个方向走
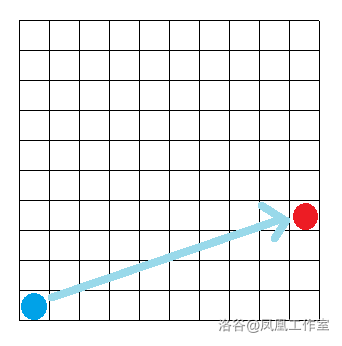
当目标点在当前位置斜方时会优先走向坐标差距大的方向,即:
当 $|x_1-x_2| \leq |y_1-y_2| $ 时向 y 方向移动
当 $|x_1-x_2| > |y_1-y_2| $ 时向 x 方向移动
也就是将下图
转化为等价的四联通路径:
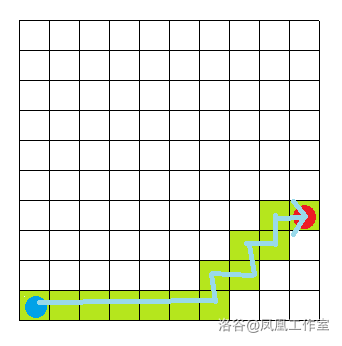
那么如果遇到了障碍呢?
只要是脑子正常的动物,遇到障碍都会绕过去(废话)
但是我们不知道向左绕和向右绕哪个是可行的,这时候我们就需要使用 BFS 对两个分支进行搜索
也就是前面是障碍时向左和右进行搜索
代码实现
寻路代码如下
#include<bits/stdc++.h>
using namespace std;
#define int long long
char mp[5005][5005];//地图,'.'为空地,'#'为障碍
bool vis[5005][5005];//标记数组
int n,m;//地图长宽
int stx,sty,edx,edy;//起点终点坐标
const int dx[]={1,0,-1,0};//位移数组
const int dy[]={0,1,0,-1};
struct node//每一个状态:位置和已经走过的路径记录
{
int x,y;
vector<pair<int,int> >pth;
};
queue<node>Q;
signed main(void)
{
cin>>n>>m>>stx>>sty>>edx>>edy;
for(int i=1;i<=n;i++)
cin>>mp[i]+1;
Q.push(node{stx,sty,{make_pair(stx,sty)}});
vis[stx][sty]=true;
while(!Q.empty())
{
int x=Q.front().x,y=Q.front().y;
vector<pair<int,int> >s=Q.front().pth;
Q.pop();
int dct;
if((edx>=x&&edy>=y&&((edx-x)>=(edy-y)))||(edx>=x&&edy<y&&((edx-x)>=(y-edy))))dct=0;
else if((edx>=x&&edy>=y&&((edx-x)<(edy-y)))||(edx<x&&edy>=y&&((x-edx)<edy-y)))dct=1;
else if((edx<x&&edy<y&&((x-edx)>=(y-edy)))||(edx<x&&edy>=y&&(x-edx)>=(edy-y)))dct=2;
else dct=3;//朝目标方向前进
int nx=x+dx[dct],ny=y+dy[dct];
if(mp[nx][ny]=='#')//如果是障碍
{
int dct1=(dct+1)%4;//向左找
if(dct1==0)dct1=4;
int nnx=x+dx[dct1],nny=y+dy[dct1];
if(!vis[nnx][nny]&&mp[nnx][nny]!='#')
{
vis[nnx][nny]=true;
s.push_back(make_pair(nnx,nny));
Q.push(node{nnx,nny,s});
if(nnx==edx&&nny==edy)
{
for(int i=0;i<s.size();i++)
cout<<s[i].first<<" "<<s[i].second<<endl;
return 0;
}
s.pop_back();
}
dct1=(dct-1+4)%4;//向右找
if(dct1==0)dct1=4;
nnx=x+dx[dct1],nny=y+dy[dct1];
if(!vis[nnx][nny]&&mp[nnx][nny]!='#')
{
vis[nnx][nny]=true;
s.push_back(make_pair(nnx,nny));
Q.push(node{nnx,nny,s});
if(nnx==edx&&nny==edy)
{
for(int i=0;i<s.size();i++)
cout<<s[i].first<<" "<<s[i].second<<endl;
return 0;
}
s.pop_back();
}
}
else//向前走
{
if(vis[nx][ny])continue;
vis[nx][ny]=true;
s.push_back(make_pair(nx,ny));
Q.push(node{nx,ny,s});
if(nx==edx&&ny==edy)
{
for(int i=0;i<s.size();i++)
cout<<s[i].first<<" "<<s[i].second<<endl;
return 0;
}
}
}
cout<<"Not found!"<<endl;
return 0;
}
看到这里,你一定发现,B* 的正确性不能验证,B* 并不是寻找最短路径,而是在最快的时间内找到一条合适的路径 (但是有些时候本来有路的 B* 并不能找到,会输出 Not Found)
实验数据表明,同等数据下,B* 速度是 A* 的 10 倍左右
对于如下的 U 型障碍,B* 会被困在里面无法出来
.......
..####.
.....#.
..####.
.......
如上情况可以自行优化(都说了不保证正确性了)
Dijkstra 寻路算法
没错,是 Dijkstra
Dijkstra 刚处理完最短路问题,就被抓来寻路了
Dijkstra 寻路其实和 A* 差不多,甚至比 A* 简单的多 (是不是讲解顺序出错了?)
算法核心
Dijkstra 利用一个优先队列维护节点,每次取出已走路程最短的节点进行拓展
也就是说,Dijkstra 找过的节点组成了一个近似圆形
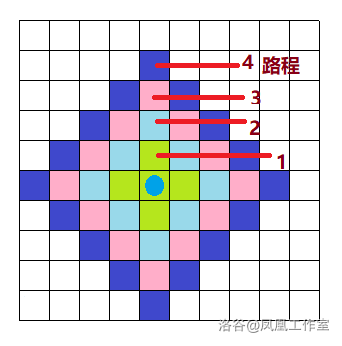
可以理解为,Dijkstra 寻路算法是启发函数 \(h(x) = 0\) 的 A*
代码应该就不用放在这了(懒得写了,反正你会 BFS)
贪心最优搜索
这个算法和 Dijkstra 寻路算法和 A* 也差不多,只不过是每次取 h(x) 函数值最小的进行拓展,即每次找预估剩余步数最少的节点进行拓展
算法缺点:
-
和 B* 一样这个算法第一次找到的终点状态不一定是最优解
-
遇到特点的障碍可能会绕路
(所以说这里章节的安排顺序可能有点问题...)
Jump Point Search (JPS) 跳点搜索
算法原理
相比于其他的搜索算法,A* 的优势在于相对智能的启发式思想,但是 A* 仍然只能像其他搜索算法一样一步只走一格,面对较大规模的数据还是会力不从心
所以跳点搜索就诞生了
跳点搜索的优势在于一次向一个方向走多格,大部分游戏中的寻路就采用了这种高效的算法
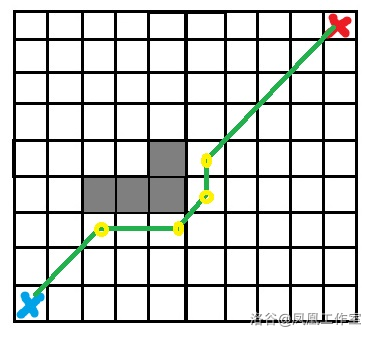
图中黄色的部分为跳点
不难发现,调点搜索依赖于网格这种结构
前置定义
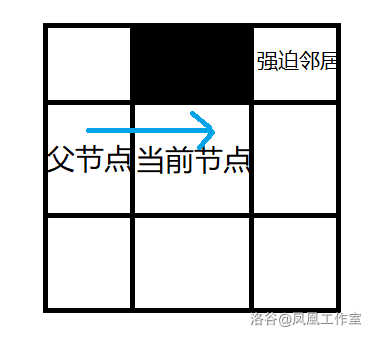
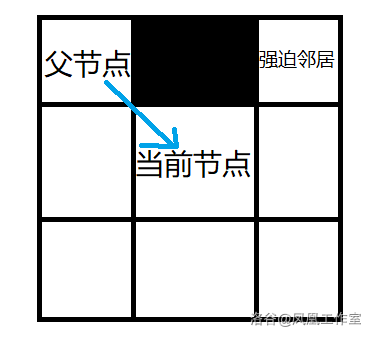
强迫邻居
定义:节点
x的 8 个邻居中有障碍,且x的父节点p经过x到达n的距离代价比不经过x到达的n的任意路径的距离代价小,则称n是x的强迫邻居。
强迫邻居用于找跳点
强迫邻居的两种情况:
1.横向
2.斜向
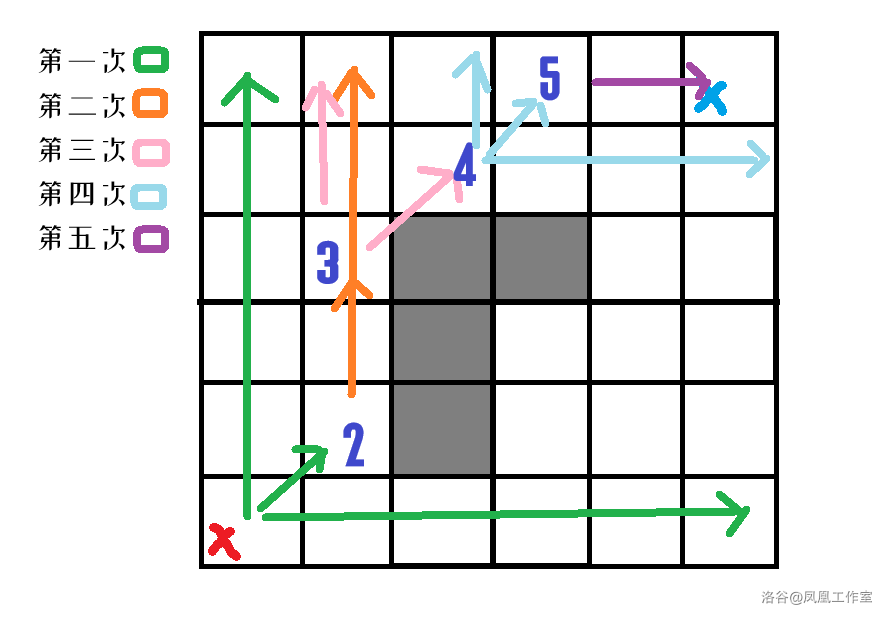
跳点
即路径中每一段的分隔,改变方向的转角处,确定每一次跳跃的终点(上图中黄色的节点)
- 如果点
y是起点或目标点,则y是跳点 - 如果
y有邻居且是强迫邻居则y是跳点 - 如果
y的父节点到y是对角线移动,并且y经过水平或垂直方向移动可以到达跳点,则y是跳点。
跳点的定义可以把整个路径想象成一根绳子,从起点和终点把他拉直,线与障碍的交点就是跳点
那么此时搜索每次展开的就是下一个跳点,使用 A* 实现
对于每次拓展的方向,因为每一次都可以跳到横纵方向所有可以跳到的位置,所以每次向斜方向跳一格,即如图所示:
代码实现
于是代码就有了:
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 105;
const int INF = 1e9;
int n, m;
char maze[MAXN][MAXN];
int dist[MAXN][MAXN];
bool vis[MAXN][MAXN];
int prex[MAXN][MAXN], prey[MAXN][MAXN];
struct Node
{
int x, y;
int g, h;
bool operator<(const Node &rhs) const
{
return g + h > rhs.g + rhs.h; // 小根堆
}
};
// 八方向
int dx[8] = {0, 0, 1, -1, 1, 1, -1, -1};
int dy[8] = {1, -1, 0, 0, 1, -1, 1, -1};
// 曼哈顿距离
int heuristic(int x, int y, int tx, int ty)
{
return abs(x - tx) + abs(y - ty);
}
// 检查是否可走
bool canMove(int x, int y)
{
return x >= 1 && x <= n && y >= 1 && y <= m && maze[x][y] == '.';
}
// JPS跳点
bool jump(int x, int y, int dx, int dy, int tx, int ty, int &jx, int &jy)
{
while (true)
{
x += dx;
y += dy;
if (!canMove(x, y))
return false;
if (x == tx && y == ty)
{
jx = x;
jy = y;
return true;
}
// 强制邻居
if ((dx == 0 || dy == 0) && ((dx == 0 && (canMove(x + 1, y) && !canMove(x + 1, y - dy))) ||
(dx == 0 && (canMove(x - 1, y) && !canMove(x - 1, y - dy))) ||
(dy == 0 && (canMove(x, y + 1) && !canMove(x - dx, y + 1))) ||
(dy == 0 && (canMove(x, y - 1) && !canMove(x - dx, y - 1)))))
{
jx = x;
jy = y;
return true;
}
// 对角线强制邻居
if (dx != 0 && dy != 0)
{
if ((canMove(x - dx, y + dy) && !canMove(x - dx, y)) ||
(canMove(x + dx, y - dy) && !canMove(x, y - dy)))
{
jx = x;
jy = y;
return true;
}
}
}
return false;
}
int main()
{
int sx, sy, tx, ty;
cin >> n >> m;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
cin >> maze[i][j];
cin >> sx >> sy >> tx >> ty;
memset(dist, 0x3f, sizeof(dist));
memset(vis, 0, sizeof(vis));
priority_queue<Node> pq;
dist[sx][sy] = 0;
pq.push({sx, sy, 0, heuristic(sx, sy, tx, ty)});
while (!pq.empty())
{
Node cur = pq.top();
pq.pop();
if (vis[cur.x][cur.y])
continue;
vis[cur.x][cur.y] = true;
if (cur.x == tx && cur.y == ty)
break;
for (int d = 0; d < 8; ++d)
{
int jx, jy;
if (jump(cur.x, cur.y, dx[d], dy[d], tx, ty, jx, jy))
{
int cost = dist[cur.x][cur.y] + max(abs(jx - cur.x), abs(jy - cur.y));//记忆化剪枝(类似最短路)
if (cost < dist[jx][jy])
{
dist[jx][jy] = cost;
prex[jx][jy] = cur.x;
prey[jx][jy] = cur.y;
pq.push({jx, jy, cost, heuristic(jx, jy, tx, ty)});
}
}
}
}
if (dist[tx][ty] >= INF)
cout << "-1\n";//无路径
else
cout << dist[tx][ty] << endl;
//由于本来存储的路径是反的,所以要反转回来
vector<pair<int, int>> path;
int px = tx, py = ty;
while (!(px == sx && py == sy))
{
path.push_back({px, py});
int nx = prex[px][py], ny = prey[px][py];
px = nx;
py = ny;
}
path.push_back({sx, sy});
//输出路径
for (auto it = path.rbegin(); it != path.rend(); ++it)
{
cout << "(" << it->first << " " << it->second << ")" << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号