蓄水池抽样算法
蓄水池抽样算法
1. 蓄水池抽样问题
从N个元素中随机的抽取k个元素,其中N无法确定。
2. n个样本中随机抽取1个(n未知)
这个问题是蓄水池抽样问题的一个特例,即 k=1。
解法:
我们总是选择第一个对象,以 1/2 的概率选择第二个,以 1/3 的概率选择第三个,依此类推,以 1/m 的概率选择第 m 个对象。当该过程结束时,每一个对象具有相同的选中概率,即 1/n,证明如下。
证明:
第 m 个对象最终被选中的概率 P = 选择 m 的概率 * 其后面所有对象不被选择的概率,即
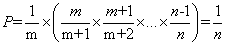
2.1 实例:链表的随机结点(leetcode382)
2.1.1 题目描述
给定一个单链表,随机选择链表的一个节点,并返回相应的节点值。保证每个节点被选的概率一样。
进阶:
如果链表十分大且长度未知,如何解决这个问题?你能否使用常数级空间复杂度实现?
2.1.2 代码实现
class Solution {
private ListNode head;
public Solution(ListNode head) {
this.head = head;
}
public int getRandom() {
int res = head.val;
ListNode p = head.next;
int i = 2;
Random random = new Random();
while(p!=null){
//生成一个[0,i)之间的随机数
if(random.nextInt(i) == 0){
res = p.val;
}
i++;
p = p.next;
}
return res;
}
}
3. n个样本随机抽取m个不同样本(n未知)
解法:
先把读到的前k个对象放入“水库”,对于第 k+1 个对象开始,以 k/(k+1) 的概率选择该对象,以 k/(k+2) 的概率选择第 k+2 个对象,以此类推,以 k/m 的概率选择第 m 个对象(m>k)。如果 m 被选中,则随机替换水库中的一个对象。最终每个对象被选中的概率均为 k/n。
证明:
第 m 个对象被选中的概率 = 选择 m 的概率(其后元素不被选择的概率+其后元素被选择的概率不替换第m个对象的概率),即
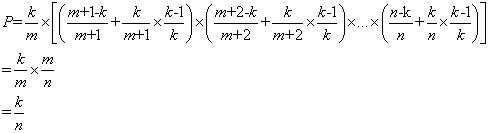


 浙公网安备 33010602011771号
浙公网安备 33010602011771号