可持久化线段树(主席树) 学习笔记
介绍
可持久化线段树,为函数式线段树,是一种支持维护和查询历史信息的线段树
其发明者为黄嘉添,由于其名字简写为hjt,因此该数据结构又被称为主席树
本质上是一个具有特殊结构的动态开点权值线段树,下面用一道例题引入
例题
给定 \(n\) 个整数构成的序列 \(a\) 和 \(m\) 个询问,每个询问对于指定的闭区间 \([l, r]\) 查询其区间内的第 \(k\) 小值。
\(1 \leq n,m \leq 2\times 10^5\),\(0\le a_i \leq 10^9\),\(1 \leq l \leq r \leq n\),\(1 \leq k \leq r - l + 1\)。
- 把往序列 \(a\) 中输入每个数转换为向序列 \(a\) 中添加一个数,由此输入序列 \(a\) 就变为了向长度为 0 的序列 \(a\) 进行 \(n\) 次操作,第 \(i\) 次操作会将 \(a_i\) 加入序列中
- 通过上述转换,我们就可以对于每一次操作在值域上建立一颗动态开点权值线段树,来维护前 \(i\)次操作中,有多少次操作添加的 \(a_i\) 在给定区间内
- 当计算区间 \([l,r]\) 的答案时,就可以拿出第 \(l-1\) 次操作时线段树和第 \(r\) 次操作时的线段树对于两者相减的值进行线段树二分(可以类比前缀和的思想)
- 具体的,处理两者相减的值时,如果该节点的左儿子维护的数的数量小于 \(k\) ,则说明第 \(k\) 小的数一定不在左子树,否则一定在右子树。根据此递归处理即可
- 上述做法若暴力实现的话则需要对于每一次操作都开一个线段树,空间肯定无法承受,所以我们需要一个更加巧妙的建树方法来处理
- 于是我们就可以通过可持久化线段树来处理
流程
- 主要思想是将压缩线段树的历史信息,将所有历史版本通过特殊结构都存到一张图上
- 容易发现每次更改一个点 \(a_i\) 时,跟随其变化而变动的线段树中的点数是 \(O(\log n)\) 级别
- 我们把这些变动的点拿出来再在旁边建树后与其原来的子节点连边,此时线段树的结构不会改变,因此就能避免建树空间过大的问题
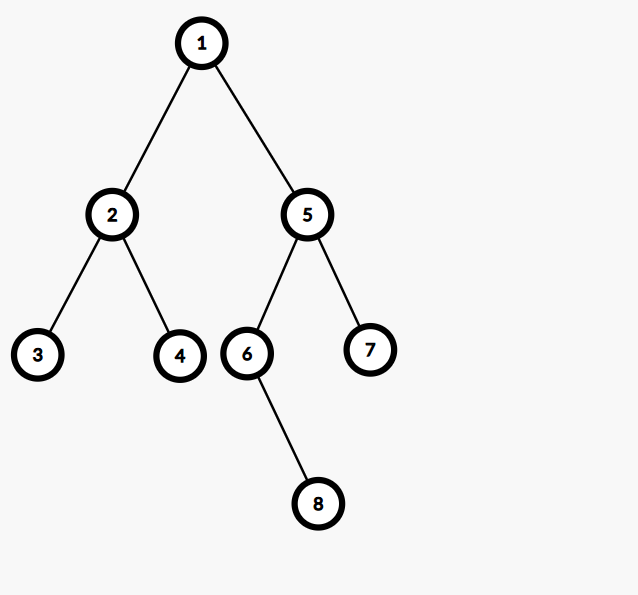
图一 原先的树
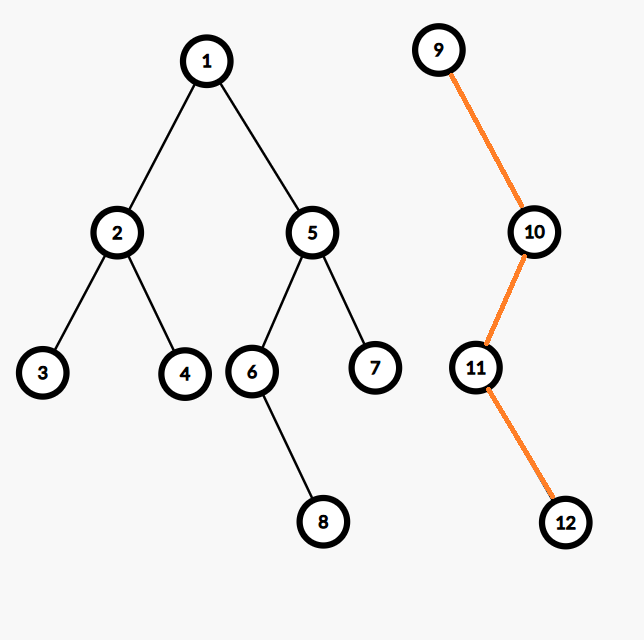
图二 此时操作了节点8,则将节点8及其影响的节点单独拿出来放到旁边
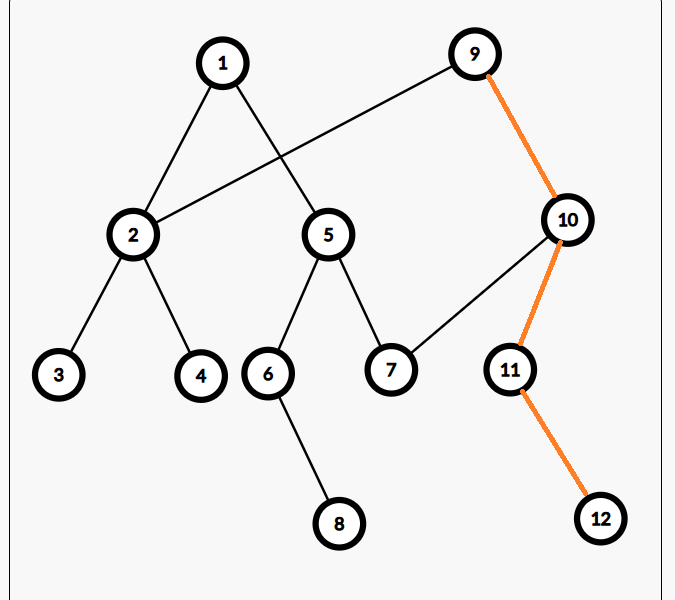
图三 为了不破坏树的性质,将影响的节点与原来的子节点连边
综上,我们就可以同过诸如此类的操作来保存线段树的不同版本从而实现可持久化
P3814 code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
void faster(){
ios_base::sync_with_stdio(false);
cout.tie(0);
cin.tie(0);
}
struct tree{
int val;//该点维护的权值
int l,r;//该点管理的区间
int ls,rs;//该点的左儿子、右儿子编号
}t[20*N];//注意空间
int n,m;
int a[N];
int b[N],cnt;//离散化后的a数组 离散化后的大小
int tot;//线段树节点个数
int root[N];//第i个版本的根节点编号
//建树
//当前节点维护区间左端点 右端点 返回当前节点的编号
int build(int l,int r){
int p=++tot;//当前节点编号
t[p]=(tree){0,l,r,0,0};//初始化
if(l==r) return p;
int mid=(l+r)/2;
t[p].ls=build(l,mid);//建左子树并记录左儿子
t[p].rs=build(mid+1,r);//建右子树并记录右儿子
return p;
}
//更改操作(创建新版本)
//当前节点 目标更改节点 增加值
int change(int x,int mb,int del){
int l=t[x].l,r=t[x].r;
int p=++tot;//创建与旧版本对应的节点
t[p]=t[x];//初始化
if(l==r){
t[p].val+=del;//若为目标节点则更改
return p;
}
int mid=(l+r)/2;
if(mb<=mid) t[p].ls=change(t[x].ls,mb,del);//递归处理左子树
else t[p].rs=change(t[x].rs,mb,del);//递归处理右子树
t[p].val=t[t[p].ls].val+t[t[p].rs].val;//更新节点信息
return p;//返回当前节点编号
}
//查询操作(线段树二分)
//版本1当前所对应的节点 版本2当前所对应的节点 第k大
int query(int bb1,int bb2,int k){
int l=t[bb1].l,r=t[bb1].r;
if(l==r) return l;
int mid=(l+r)/2;
int u=t[t[bb1].ls].val-t[t[bb2].ls].val;//相减操作,类比于前缀和
if(k<=u) return query(t[bb1].ls,t[bb2].ls,k);//如果左子树所包含节点大于等于k,则第k大点在左子树里,此时递归处理左子树
else return query(t[bb1].rs,t[bb2].rs,k-u);//同上
}
signed main()
{
faster();
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
b[++cnt]=a[i];
}
sort(b+1,b+cnt+1);//排序
cnt=unique(b+1,b+cnt+1)-b-1;//去重
root[0]=build(1,cnt);//建立最初版本(未经任何修改)
for(int i=1;i<=n;i++){
int x=lower_bound(b+1,b+cnt+1,a[i])-b;
root[i]=change(root[i-1],x,1);//建立[1,a[i]]之间的版本
}
for(int i=1;i<=m;i++){
int l,r,k;
cin>>l>>r>>k;
int ans=query(root[r],root[l-1],k);//类比于前缀和
cout<<b[ans]<<"\n";
}
return 0;
}
习题
P2633 Count on a tree
给定一棵 \(n\) 个节点的树,每个点有一个权值。
有 \(m\) 个询问,每次给你 \(u,v,k\),你需要回答 \(u\) 和 \(v\) 这两个节点间第 \(k\) 小的点权。
强制在线,\(1\le n,m \le 10^5\),点权在 \([1, 2 ^ {31} - 1]\)
- 在树上的每个节点建立一个主席树维护从根节点到当前节点的值域,值域较大,因此要离散化后做
- 依据前面主席树的答案计算方式,我们参照树上差分的思想,对于每一次查询都转化为 \(k\) 与 \(S_u+S_v-S_{lca_{u,v}}-S_{fa[lca_{u,v}]}\) 之间的比较( \(S_i\) 代表 \(i\) 节点上的"前缀"主席树)
- lca套个倍增法上去,那么就做完了
- 时间复杂度 \(O(n \log n)\)
P2633 code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+5;
void faster(){
ios_base::sync_with_stdio(false);
cout.tie(0);
cin.tie(0);
}
struct edge{
int v,nxt;
}ed[N];
struct tree{
int val;
int l,r;
int ls,rs;
}t[20*N];
int n,m,en,first[N];
int a[N],b[N],cnt;//原数组 离散化后数组 离散化后数组个数
//主席树节点总个数 主席树每个版本的根节点编号 原图每个节点深度 原图每个节点父亲编号 a数组中值离散化后在b数组的位置 求lca数组
int tot,root[N],dep[N],faa[N],pos[N],fax[N][22];
void add_edge(int u,int v){
ed[++en].nxt=first[u];
first[u]=en;
ed[en].v=v;
}
int build(int l,int r){
int p=++tot;
t[p]=(tree){0,l,r,0,0};
if(l==r) return p;
int mid=(l+r)>>1;
t[p].ls=build(l,mid);
t[p].rs=build(mid+1,r);
return p;
}
int change(int x,int mb,int del){
int p=++tot;
t[p]=t[x];
int l=t[p].l,r=t[p].r;
if(l==r){
t[p].val+=del;
return p;
}
int mid=(l+r)>>1;
if(mb<=mid) t[p].ls=change(t[x].ls,mb,del);
else t[p].rs=change(t[x].rs,mb,del);
t[p].val=t[t[p].ls].val+t[t[p].rs].val;
return p;
}
int query(int bb1,int bb2,int bb3,int bb4,int k){//u节点 v节点 u与v的lca u与v的lca的父节点
int l=t[bb1].l,r=t[bb1].r;
if(l==r) return l;
int u=t[t[bb1].ls].val+t[t[bb2].ls].val-t[t[bb3].ls].val-t[t[bb4].ls].val;
if(k<=u) return query(t[bb1].ls,t[bb2].ls,t[bb3].ls,t[bb4].ls,k);
else return query(t[bb1].rs,t[bb2].rs,t[bb3].rs,t[bb4].rs,k-u);
}
void dfs(int x,int fa){//第一遍dfs,预处理出原图lca
dep[x]=dep[fa]+1;
faa[x]=fa;
fax[x][0]=fa;
for(int i=1;(1<<i)<=dep[x];i++) fax[x][i]=fax[fax[x][i-1]][i-1];
for(int i=first[x];i!=0;i=ed[i].nxt){
int d=ed[i].v;
if(d!=fa) dfs(d,x);
}
}
void dfs2(int x){//第二遍dfs,对每个节点建前缀主席树
root[x]=change(root[faa[x]],pos[x],1);//对于每个节点,建树时根据其父亲建
for(int i=first[x];i!=0;i=ed[i].nxt){
int d=ed[i].v;
if(d!=faa[x]) dfs2(d);
}
}
int lca(int x,int y){//求lca
if(dep[x]<dep[y]) swap(x,y);
for(int i=20;i>=0;i--) if(dep[y]<=dep[x]-(1<<i)) x=fax[x][i];
if(x==y) return x;
for(int i=20;i>=0;i--){
if(fax[x][i]==fax[y][i]) continue;
else{
x=fax[x][i];
y=fax[y][i];
}
}
return fax[x][0];
}
signed main()
{
faster();
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
b[++cnt]=a[i];
}
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
add_edge(u,v);
add_edge(v,u);
}
dfs(1,0);
sort(b+1,b+cnt+1);//离散化
cnt=unique(b+1,b+cnt+1)-b-1;
for(int i=1;i<=n;i++){
int x=lower_bound(b+1,b+cnt+1,a[i])-b;//预处理出a数组离散化后在b数组位置
pos[i]=x;
}
root[0]=build(1,cnt);//建立初始版本
dfs2(1);
int lst=0;
for(int i=1;i<=m;i++){
int l,r,x;
cin>>l>>r>>x;
l=(l^lst);
if(l>r) swap(l,r);
int u=lca(l,r),v=faa[u];
int ans=query(root[l],root[r],root[u],root[v],x);
cout<<b[ans]<<"\n";
lst=b[ans];
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号