2025 SDSC 题目整合
Day1 T1
有一个长为 \(n\) 的序列 \(a\) ,其价值为所有数的最大公约数。
可以进行一次操作,选择序列中的一个区间 \([l,r]\) ,将区间中的每个数字加上给定常数 \(k\) ,也可以不操作。
求序列价值最大值。
- 令 \(f(l,r)\) 为序列 \(a\) 中, \(a_l\) 到 \(a_r\) 之间的数加上 \(k\) 后的gcd
- 每一个方案可以分成三部分:前缀 \([1,l)\) ,\(f[l,r]\) , 后缀 \((r,n]\)
- 注意到前缀gcd一定是一段一段逐渐下降的。最优答案一定是某一段中 \(l\) 最大的
- 只有每个段中 \(l\) 最大(最靠右)的点有用,这样的点最多有 \(\log (v)\) 个(点 \(r\) 同理)
- 因此枚举每个这样的 \(l\) ,然后暴力枚举 \(r\) ,求最小答案即可。
code
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=7e6+5;
int t,n,k;
int a[N],pre[N],sup[N];//数组 前缀gcd 后缀gcd
int l[N],cnt;//每一个有用的点l
int gcd(int a,int b){
if(b==0) return a;
else return gcd(b,a%b);
}
signed main(){
cin>>t;
while(t--){
cin>>n>>k;
for(int i=1;i<=n;i++) cin>>a[i];
pre[0]=sup[n+1]=0;
cnt=0;
for(int i=1;i<=n;i++){
pre[i]=gcd(a[i],pre[i-1]);
if(pre[i]!=pre[i-1]) l[++cnt]=i-1;
}
for(int i=n;i>=1;i--) sup[i]=gcd(a[i],sup[i+1]);
int ans=sup[1];
for(int i=1;i<=cnt;i++){//枚举每一个有用的点l
int now=pre[l[i]];
for(int j=l[i]+1;j<=n;j++){//暴力枚举r
if(now==0) now=a[j]+k;
ans=max(ans,gcd(now,sup[j]));
now=gcd(now,a[j]+k);
}
ans=max(ans,now);
}
cout<<ans<<"\n";
}
return 0;
}
Day2 T1
有一个长为 \(n\) 的小写字母字符串 \(s=s_1s_2...s_n\)。
对于每个 \(1≤l≤r≤n\) ,进行以下操作生成一个新字符串:
- 删除 \([l,r]\) 位置的子串,将剩下两边字符串拼接起来,最终得到新字符串为 \(s_1s_2 ...s_l−1s_r+1 ...s_n\)
请求出在 \(\dfrac{n(n+1)}{2}\) 个生成的新字符串中本质不同字符串的数量。
- 首先考虑在什么条件下删除两个子串所得到的新字符串的本质相同

- 如上图,很明显注意到当删除两端区间时,剩下新字符串的公有前缀和公有后缀一定相同(即黑色段),那么当浅灰色段和深灰色段相同时,这两个新字符串才相同
- 将浅灰色段、深灰色段看做两个字符,那么就能得到一个结论
字符串中每一对相同的字符都会产生一对相同的新字符串 - 那么产生的总新字符串减去重复字符串的对数即为答案
- 由此易得答案为 \(\dfrac{n(n+1)}{2}-\large\sum\limits_{i=a}^{z} \dfrac{c_i*(c_i-1)}{2}\) ,其中 \(c_i\) 为字符 \(i\) 在字符串 \(s\) 中的出现次数
Day2 T2
有一个包含 \(n\) 个点和 \(m\) 条边的联通无向图 \(G\) ,每条边的边权都是 1。
每个点有黑白两种颜色。建立一个新的完全图 \(H\) 包含所有黑色点,每两个黑色点之间的边权为原图 \(G\) 上两点之间最短路长度。
求 \(H\) 的最小生成树的边权和。
- 一个很明显的思路是从每个黑点向其他黑点进行01bfs求距离,然后暴力建图,最后对这张图跑个kruskal最小生成树即可
- 时间复杂度是 \(O(n^2)\) ,明显不能接受
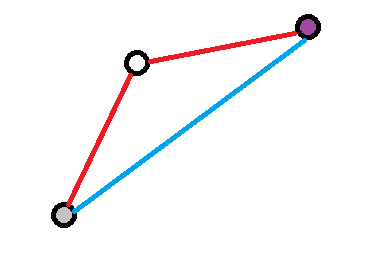
- 考虑上图情况,根据 kruscal 过程从小到大考虑每条边,一定是两条红边在蓝边前先被考虑,所以蓝边一定没用。
- 所以对于一个黑点建边时,可以只建那些 与这个黑点之间 没有间隔任何黑点 的点 的边
- 具体做法为每次更新对每个黑点向周围扩展一层,若发现一个点同时被两个黑点扩展到了,则向这两个黑点之间连一条边
- 这样处理最终出现在最小生成树中的边最多有 \(O(m)\) 个,时间复杂度 \(O(m\log m)\)
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
struct edge{
int v,w;
int next;
}ed[N];
struct edge2{
int u,v,val;
};
int t,first[N],en,n,m,cnt,ztt[N],dist[N],col[N],bcj[N];//后四个数组意义分别为哪些点为黑点,非黑点到离它最近的黑点的距离,这个点由哪个黑点扩展而来,并查集(kruskal时用)
char zt[N];
queue<int> q;
bool operator >(edge2 a,edge2 b){
return a.val>b.val;
}
priority_queue<edge2,vector<edge2>,greater<edge2> > p;
int go(int x){
if(bcj[x]==x) return x;
else return bcj[x]=go(bcj[x]);
}
bool merge(int x,int y){
int a=go(x),b=go(y);
if(a==b) return 0;
else {
bcj[a]=b;
return 1;
}
}
void add_edge(int u,int v){
ed[++en].next=first[u];
first[u]=en;
ed[en].v=v;
ed[en].w=1;
}
signed main()
{
cin>>t;
while(t--){
cnt=en=0;
cin>>n>>m;
cin>>zt;
for(int i=1;i<=n;i++) first[i]=0;
for(int i=1;i<=n;i++) if(zt[i-1]-'0'==1) ztt[++cnt]=i;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
add_edge(u,v);
add_edge(v,u);
}
while(q.size()) q.pop();
for(int i=1;i<=n;i++) col[i]=dist[i]=0;
for(int i=1;i<=cnt;i++){
q.push(ztt[i]);
col[ztt[i]]=i;
}
while(q.size()){
int x=q.front();
q.pop();
for(int i=first[x];i!=0;i=ed[i].next){
int d=ed[i].v;
if(col[d]){
if(col[d]==col[x]) continue;
p.push((edge2){col[x],col[d],dist[x]+dist[d]+1});//向最小生成树内加入答案
}
else{
dist[d]=dist[x]+1;
col[d]=col[x];
q.push(d);
}
}
}
for(int i=1;i<=cnt;i++) bcj[i]=i;
int sum=0,ans=0;
while(p.size()){//kruskal
int l=p.top().u,r=p.top().v;
int dd=p.top().val;
p.pop();
if(merge(l,r)){
ans+=dd;
}
}
cout<<ans<<"\n";
}
return 0;
}
Day3 T1
你有一个字符串 \(s\) ,其中有一些方括号和圆括号,以及小写字母
a到z。
从内到外,从左到右,去掉括号
每去掉一个方括号就把括号所包含的区间内的字符串反转
去掉一个圆括号就将括号所包含的区间内的所有字符+1(a到b,b到c,c到d...)
输出最后的字符串。
保证 \(s\) 去掉小写字母之后剩下的是一个合法的括号序列。
- 根据题目得不会出现
[(])这种情况 - 注意到先去掉所有圆括号并不会影响后续方括号操作,因此通过一个差分先将所有圆括号操作处理完
- 对于没有原括号的字符串从头遍历,每遇到一个方括号就将当前遍历方向翻转并移到这对方括号的末尾遍历
- 例如:
a[b[cd]e]
遍历下标顺序为 1->5->3->4->2 (仅包括字母的下标)
- 最后加上差分答案并按照方括号顺序遍历输出即可
code
#include<bits/stdc++.h>
using namespace std;
const int N=5e6+5;
char s[N];
int n,a[N],top;
int cf[N];//差分数组
int pos[N];//若S_i为向右的方括号,则pos_i为其所对应的向左的方括号的下标
stack<int> st;//栈,用来处理方括号的操作
void dfs(int x,int zt){//当前遍历下标 当前遍历顺序(-1为倒着遍历,1为正着遍历)
if(zt==1){
while(x<=n&&s[x]!=']'){
if(s[x]=='['){
dfs(pos[x]-1,-1);//翻转方向,并改变下标
x=pos[x];//跳过这一段已经遍历完的区间
}
else if('a'<=s[x]&&s[x]<='z') cout<<(char)(a[x]-1+'a');
x++;
}
}
if(zt==-1){
while(x>=1&&s[x]!='['){
if(s[x]==']'){
dfs(pos[x]+1,1);
x=pos[x];
}
else if('a'<=s[x]&&s[x]<='z') cout<<(char)(a[x]-1+'a');
x--;
}
}
}
signed main()
{
cin>>s;
n=strlen(s);
for(int i=n+1;i>=1;i--) s[i]=s[i-1];
for(int i=1;i<=n;i++){//差分
if('a'<=s[i]&&s[i]<='z') a[i]=s[i]-'a'+1;
else if(s[i]=='['||s[i]==']') a[i]=s[i];
else if(s[i]=='(') cf[i]++;
else cf[i+1]--;
}
for(int i=1;i<=n;i++){//加上差分数组
cf[i]+=cf[i-1];
a[i]+=cf[i];
}
for(int i=1;i<=n;i++){//去掉圆括号后重新处理数组
if(s[i]=='['||s[i]==']') a[i]=0;
else{
while(a[i]>=27) a[i]-=26;
if(a[i]>=27) a[i]%=26;
}
}
for(int i=1;i<=n;i++){//找到每对方括号的位置
if(s[i]=='[') st.push(i);
else if(s[i]==']'){
int x=st.top();
pos[x]=i;
pos[i]=x;
st.pop();
}
}
dfs(1,1);//按方括号顺序遍历
return 0;
}
Day4 T1
给一棵 \(1\) 为根的树,每个点有一种颜色 \(a_i\)
求每个子树中颜色出现次数的中位数乘 \(2\)(未出现的颜色不计数).
前置知识:
树上启发式合并(dsu on tree),其模版为P9233 颜色平衡树
具体学习可以看这个博客
- 对于每一个节点其答案的合并可以采取树上启发式合并,那么现在考虑一下具体怎么合并
- 容易发现当将某个节点加入当前答案时,我们并不关心它的颜色究竟是什么,我们只关心它所属的颜色加入前后的位置排名会怎么变化
- 由于每次只加入一个节点,容易发现该节点所属颜色的数量只会变化一,所以我们采取如下做法:
- 设置数组 \(L_i,R_i\) ,代表目前数量为 \(i\) 的颜色在目前总排名榜上的左下标和右下标
- 例如
1 2 2 2 3,其中 \(L_2=2,R_2=4\) - 令 \(col_i\) 为颜色为 \(i\) 的节点的个数,那么当加入节点颜色为 \(u\) 时,只需要将 \(R_{col_u}\)减一,\(L_{{col_u}+1}\)减一
- 这样我们就得到了一个时间复杂度为 \(O(n\log n)\) 的算法(启发式合并 \(O(n\log n)\) ,答案计算 \(O(n)\) )
code
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
struct edge{
int v,next;
}ed[N];
int en,first[N];
int n,a[N];
//节点颜色个数排行榜 左下标 右下标 颜色为i的节点有多少个 子树i的大小 i的重儿子 答案
int tmp[N],L[N],R[N],cnt[N],siz[N],son[N],ans[N];
void add_edge(int u,int v){
ed[++en].next=first[u];
first[u]=en;
ed[en].v=v;
}
void bigdfs(int x,int fa){
for(int i=first[x];i!=0;i=ed[i].next){
int d=ed[i].v;
if(d!=fa){
bigdfs(d,x);
if(siz[d]>=siz[son[x]]) son[x]=d;
siz[x]+=siz[d];
}
}
}
void add(int x){//加入节点答案
R[cnt[a[x]]]--;
cnt[a[x]]++;
L[cnt[a[x]]]--;
tmp[L[cnt[a[x]]]]=cnt[a[x]];
}
void del(int x){//回溯,消除节点对答案的影响
L[cnt[a[x]]]++;
cnt[a[x]]--;
R[cnt[a[x]]]++;
tmp[R[cnt[a[x]]]]=cnt[a[x]];
}
void del_tree(int x,int fa){//消除子树x对答案的影响
del(x);
for(int i=first[x];i!=0;i=ed[i].next){
int d=ed[i].v;
if(d!=fa) del_tree(d,x);
}
}
void lightdfs(int x,int fa){//加入子树x对答案的影响
add(x);
for(int i=first[x];i!=0;i=ed[i].next){
int d=ed[i].v;
if(d!=fa) lightdfs(d,x);
}
}
void dsu(int x,int fa){//树上启发式合并
for(int i=first[x];i!=0;i=ed[i].next){
int d=ed[i].v;
if(d!=fa&&d!=son[x]){
dsu(d,x);
del_tree(d,x);
}
}
if(son[x]) dsu(son[x],x);
add(x);
int u=0;
for(int i=first[x];i!=0;i=ed[i].next){
int d=ed[i].v;
if(d!=fa&&d!=son[x]) lightdfs(d,x);}
}
if((R[n]-L[1]+1)%2==1) u=tmp[(L[1]+R[n])/2]*2;
else u=tmp[(L[1]+R[n])/2]+tmp[(L[1]+R[n])/2+1];
ans[x]=u;
}
signed main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
add_edge(u,v);
add_edge(v,u);
}
for(int i=1;i<=n;i++) siz[i]=1;
bigdfs(1,0);
for(int i=0;i<=n;i++){
L[i]=n+1;
R[i]=n;
}
L[0]=1;
dsu(1,0);
for(int i=1;i<=n;i++) cout<<ans[i]<<' ';
return 0;
}
彩蛋:
可以看到出题人对数据十分用心...

Day6 T1(47分做法)
给定一个序列 \(a_1,a_2,...,a_n\),你需要从这个序列中选出恰好 \(k\) 个不相交的子段,使得每个子段的长度都是质数。
设其中第 \(i\) 个子段的元素之和是 \(s_i\),你需要最大化 \(\min (s_1,s_2,...,s_k)\)。
这个问题太难了,所以保证所有数据的 \(a_i\) 都在 \([−1000,1000]\) 中随机生成。
- 最大化最小值,显然二分
- 直接二分答案,那么问题转化为了判断是否存在一种合法方案使得其中最小和为 \(mid\)
- 从前往后贪心,对于每个位置 \(i\),设上次选择的段的右端点是 \(k\) ,
- 如果存在一个 \(j∈[k,i)\) 使得 \(i−j\) 是质数并且 \(s_i−s_j≥mid\) ,就可以新划分出一段。(<-止步于此)
- 用 set 按照 \(s_j\) 从小到大维护 \([k,i)\) 中的 \(j\),每次只需要从 set 的开头依次枚举 set 中的元素
- 由于质数的分布,以及 set 中元素的顺序是随机的,所以期望 \(O(\log n)\) 次即可枚举到一个 \(i−j\) 是质数的 \(j\)。
- 时间复杂度 \(O(n \log n \log (nV))\)。
47分code
//然而并没有什么好说的
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
bool privis[N];
int n,k,a[N],qzh[N],l=-2e8,r=2e8;
bool check(int x){
int ans=0,lst=0;
for(int i=1;i<=n;i++){
for(int j=lst+1;j<=i;j++){
if(privis[i-j+1]&&qzh[i]-qzh[j-1]>=x){
lst=i;
ans++;
break;
}
}
}
if(ans>=k) return 1;
return 0;
}
signed main()
{
cin>>n>>k;
privis[1]=0;//筛法
for(int i=2;i<=n;i++) privis[i]=1;
for(int i=2;i<=n;i++){
if(privis[i]){
for(int j=2;i*j<=n;j++) privis[i*j]=0;
}
}
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) qzh[i]=qzh[i-1]+a[i];
int anss=0;
while(l<=r){
int mid=(l+r)/2;
if(check(mid)){
anss=mid;
l=mid+1;
}
else r=mid-1;
}
if(l==-2e8||r==2e8) cout<<-1;
else cout<<anss;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号