2024 平邑一中集训 笔记(上)
Day2
T1
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
int n,m;
vector<int> v;
int ans;
map<vector<int>,int> ma;
bool check(){
for(int i=0;i<m;i++) if(v[i]!=0) return 1;
return 0;
}
signed main(){
cin>>n>>m;
for(int i=1;i<=m+10;i++){
v.push_back(0);
}
ma[v]=0;
for(int i=1;i<=n;i++){
int u;
cin>>u;
for(int j=0;j<m;j++){
if(u&(1<<j)){
v[j]++;
}
}
for(int j=m-1;j>=0;j--){
v[j]-=v[0];
}
if(!ma.count(v)&&check()) ma[v]=i;
ans=max(ans,i-ma[v]);
}
cout<<ans;
return 0;
}
T2
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
#define int long long
int n;
pair<int,int> w[N];
bool cmp(pair<int,int> a,pair<int,int> b){
if(a.first<a.second){
if(b.first<b.second) return a.first<b.first;
return 1;
}
else {
if(b.first<b.second) return 0;
return a.second>b.second;
}
}
signed main(){
//freopen("wash.in", "r", stdin);
//freopen("wash.out", "w", stdout);
cin>>n;
for(int i=1;i<=n;i++){
cin>>w[i].first>>w[i].second;
}
sort(w+1,w+n+1,cmp);
/*
for(int i=1;i<=n;i++){
cout<<w[i].first<<' '<<w[i].second<<"\n";
}
cout<<"\n";
*/
int cnt1=0,cnt2=0;
for(int i=1;i<=n;i++){
cnt1+=w[i].first;
cnt2=max(cnt2,cnt1)+w[i].second;
//cout<<cnt1<<' '<<cnt2<<"\n";
}
//cout<<cnt1<<' '<<cnt2<<"\n";
cout<<cnt2;
return 0;
}
/*
4
1 3
2 2
2 9
12 6
*/
Day3
T1
题面：
观察得知:
当 \(a_i\) 与 \(a_j\) 二进制位数相同时，\(a_i\) \(\&\) \(a_j\) \(\geq\) \(a_i\) ^ \(a_j\)
-
所以我们可以先处理出所有 \(a_i\) 的二进制位数，将其排序
-
然后对于每个位数相等的区间计算其对答案的贡献（能使答案增加多少）
-
例如：
对于序列：
1 3 2 3 5 7 7 9
二进制转换后:
1 11 10 11 101 111 111 1001
每个的二进制位数
1 2 2 2 3 3 3 4
每个位数相等的区间长度为
1 3 3 1
根据上述得出的结论，那么：
\(ans\) = \(C^2_1\) \(+\) \(C^2_3\) \(+\) \(C^2_3\) \(+\) \(C^2_1\)
\(ans\) = \(0\) \(+\) \(\frac{3!}{(3-2)!*2!}\) \(+\) \(\frac{3!}{(3-2)!*2!}\) \(+\) \(0\) \(=\) \(3\) \(+\) \(3\) \(=\) \(6\)
- 由此可得，每个区间对答案的贡献为 \(C^2_{len}\) \(=\) \(\frac{len!}{(len-2)!*2!}\) \(=\) \(\frac{len*(len-1)}{2}\)
- \(O(n)\)求一遍即可
点击查看代码
#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<stack>
#include<stdio.h>
#include<cstring>
#include<math.h>
#include<iomanip>
#include<algorithm>
#define int long long
using namespace std;
const int N=1e5+5;
void faster(){
ios_base::sync_with_stdio(false);
cout.tie(0);
cin.tie(0);
}
int t;
int n;
int a[N];
int now[N];
int ans=0;
int cnt;
int zgw(int u){
for(int i=30;i>=0;i--){
if(u&(1<<i)) return i;
}
}
signed main()
{
//faster();
//freopen("calc.in","r",stdin);
//freopen("calc.out","w",stdout);
cin>>t;
while(t--){
cin>>n;
ans=0;
int maxx=-1;
for(int i=1;i<=n;i++){
cin>>a[i];
now[i]=zgw(a[i]);
}
sort(now+1,now+n+1);
cnt=1;
for(int i=2;i<=n;i++){
if(now[i]!=now[i-1]){
ans+=cnt*(cnt-1)/2;
cnt=0;
}
cnt++;
}
ans+=cnt*(cnt-1)/2;
cout<<ans<<"\n";
}
return 0;
}
/*
Cm,n
n!/(n-2)!*2
(n!/(n-2)!)/2
n*(n-1)/2
*/
T2
- 把台阶看成节点，与传送门看成边权为0的边，与能一步到达的位置看成边。
可以看出这题要用分层图最短路求解 - 分层图最短路模版:P4568 [JLOI2011] 飞行路线
P4568代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e6+5;
int n,m,k;
int s,t;
int dist[N];
bool vis[N];
vector<pair<int,int> > tu[N];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
void add_edge(int u,int v,int w){
tu[u].push_back({w,v});
}
void dijkstra(int st){
memset(dist,0x3f3f3f3f,sizeof(dist));
dist[st]=0;
q.push({0,st});
while(q.size()){
//cout<<q.size()<<"\n";
/*while(vis[q.top().second]){
q.pop();
}*/
//cout<<q.size()<<"\n";
int u=q.top().second;
q.pop();
if(!vis[u]) vis[u]=1;
else continue;
int siz=tu[u].size();
for(int j=0;j<siz;j++){
int v=tu[u][j].second;
int b=tu[u][j].first;
if(dist[v]>dist[u]+b){
dist[v]=dist[u]+b;
q.push({dist[v],v});
}
//cout<<" "<<q.size()<<"\n";
}
}
return ;
}
signed main()
{
cin>>n>>m>>k;
cin>>s>>t;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
for(int j=0;j<=k;j++){
add_edge(u+n*j,v+n*j,w);
add_edge(v+n*j,u+n*j,w);
if(j!=k){
add_edge(u+n*j,v+n*(j+1),0);
add_edge(v+n*j,u+n*(j+1),0);
}
}
}
for(int i=1;i<=k;i++) add_edge(t+(i-1)*n,t+i*n,0);
dijkstra(s);
cout<<dist[t+k*n];
return 0;
}
- 由于数据范围大，用
dijkstra跑这个分层图会超时 - 注意与到能一步到达的位置可以看成边权为1的边，与传送门可以看成边权为0的边，而
dijkstra的堆存这些又太浪费空间了 - 由此可以用双端队列代替堆，0的插入前面，1的插入后面。这就是
01BFS - 01BFS模版题：P4554 小明的游戏
P4554 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=500+5;
int n,m;
int sx,sy;
int tx,ty;
bool mapp[N][N];
int dist[N][N];
bool vis[N][N];
int dx[]={0,1,0,-1,0};
int dy[]={0,0,-1,0,1};
deque<pair<int,int> > q;
bool check(int a,int b){
if(a<=n&&b<=m&&a>=1&&b>=1) return 1;
else return 0;
}
int bfs(int x,int y){
dist[x][y]=0;
q.push_back({x,y});
while(q.size()){
int xx=q.front().first;
int yy=q.front().second;
q.pop_front();
if(!vis[xx][yy]) vis[xx][yy]=1;
else continue;
for(int i=1;i<=4;i++){
int xxx=xx+dx[i];
int yyy=yy+dy[i];
if(check(xxx,yyy)){
if(mapp[xxx][yyy]!=mapp[xx][yy]&&dist[xxx][yyy]>dist[xx][yy]+1){
dist[xxx][yyy]=dist[xx][yy]+1;
q.push_back({xxx,yyy});
}
if(mapp[xxx][yyy]==mapp[xx][yy]&&dist[xxx][yyy]>dist[xx][yy]){
dist[xxx][yyy]=dist[xx][yy];
q.push_front({xxx,yyy});
}
}
}
}
return dist[tx][ty];
}
signed main()
{
while(cin>>n>>m&&n!=0){
char a[N];
memset(vis,0,sizeof(vis));
memset(mapp,0,sizeof(mapp));
memset(dist,0x3f3f3f3f,sizeof(dist));
for(int i=1;i<=n;i++){
cin>>a+1;
for(int j=1;j<=m;j++){
if(a[j]=='@')mapp[i][j]=1;
else mapp[i][j]=0;
}
}
cin>>sx>>sy>>tx>>ty;
sx++,sy++;
tx++,ty++;
cout<<bfs(sx,sy)<<"\n";
}
return 0;
}
把以上两个思路结合起来即为正解
没写代码
Day4
因为调CF1612E调了一晚上没调出来，被气疯了，不写了
Day5
树的直径
树的直径为树上距离最长两点的距离
树形dp求直径
略，因为我懒得用
贪心求直径
- 先从根节点dfs找到与根节点距离最长的点 \(p\)
- 再从点 \(p\) 出发找到距离最长的点 \(q\)
- \(p-q\) 为树的直径
例题：
该题目唯一难点在于读懂题意
- 数据范围 \(N \leq 300\) ,考虑暴力
- 先求出直径，暴力枚举直径上的端点作树网的核，dfs求出该种情况的偏心距，记录答案。
- 将所有记录偏心距取最小的答案即可
- 时间复杂度 \(O(n^3)\)
一些特别牛逼的事
该题最终可以优化到：
\(O(n^3)\)->\(O(n^2)\)->\(O(n\log_n)\)->\(O(n)\)
最近公共祖先(LCA)
指树上两个节点他们共同祖先中离他们最近的第一个祖先
实现
- 设 \(f[i][k]\) 为节点 \(i\) 往上跳 \(2^k\) 步的点
- 则有递推式 \(f[i][k]=f[f[i][k-1]][k-1]\)
- 可用倍增求解，向上跳直到两点深度相同为止，检测一个点是否是另一个点的祖先，否则继续向上跳，一直到在两点即将汇合的位置前一个点停下。所得答案即为 \(f[a][0]\)
- 复杂度为 \(O(n\log n)\)
模版：P3379
点击查看代码
#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<stack>
#include<stdio.h>
#include<cstring>
#include<math.h>
#include<iomanip>
#include<algorithm>
#define int long long
using namespace std;
const int N=5e5+5;
void faster(){
ios_base::sync_with_stdio(false);
cout.tie(0);
cin.tie(0);
}
int n,m,s;
vector<int> tu[N];
int dep[N];
int f[N][21];
bool vis[N];
void dfs(int x,int lst){
dep[x]=dep[lst]+1;
vis[x]=1;
f[x][0]=lst;
for(int i=1;(1<<i)<=dep[x];i++){
f[x][i]=f[f[x][i-1]][i-1];
}
for(int i=0;i<tu[x].size();i++){
int u=tu[x][i];
if(!vis[u]){
dfs(u,x);
}
}
}
int Lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(int i=20;i>=0;i--){
if(dep[y]<=dep[x]-(1<<i)){
x=f[x][i];
}
}
if(x==y) return x;
for(int i=20;i>=0;i--){
if(f[x][i]==f[y][i]) continue;
else{
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
signed main()
{
//faster();
cin>>n>>m>>s;
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
tu[u].push_back(v);
tu[v].push_back(u);
}
dfs(s,0);
for(int i=1;i<=m;i++){
int a,b;
cin>>a>>b;
cout<<Lca(a,b)<<"\n";
}
return 0;
}
树上差分
给定一棵树，将进行 \(k\) 次操作，每次操作给定两个节点 \(x,y\) 。
需要将这两个节点之间的路径上的点的点权全部增加1(包括两个节点)。
求 \(k\) 次操作后每个点的点权是多少
树上差分用于快速求解这样的问题
思路
- 设 \(ans[i]\) 为编号为k的点最终的点权
- 易得 \(x - y\) 的路径必经过 \(lca(x,y)\)，所以可以先求出 \(lca(x,y)\) ，然后将
ans[x]++,ans[y]++，最后计算时将节点的各子树的答案合并即可。 - 但是这样做法有一个问题，最后计算 \(ans[lca(x,y)]\) 会重复加两次
即：当ans[x]=1,ans[y]=1时，\(ans[lca(x+y)]=ans[x]+ans[y]=2\) - 而我们只想使 \(x-lca(x,y)-y\) 上每个节点仅加一次
- 因此在操作后可以将
lca(x,y)--和 \(lca(x,y)\) 的父节点的值减一，以此完全消除当前操作对后续的影响
我在说些什么
代码
#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<stack>
#include<stdio.h>
#include<cstring>
#include<math.h>
#include<iomanip>
#include<algorithm>
#define int long long
using namespace std;
const int N=5e4+5;
void faster(){
ios_base::sync_with_stdio(false);
cout.tie(0);
cin.tie(0);
}
int n,k;
vector<int> tu[N];
int dep[N];
int f[N][21];
bool vis[N];
int cnt[N];
void dfs(int x,int lst){
dep[x]=dep[lst]+1;
vis[x]=1;
f[x][0]=lst;
for(int i=1;(1<<i)<=dep[x];i++){
f[x][i]=f[f[x][i-1]][i-1];
}
for(int i=0;i<tu[x].size();i++){
int u=tu[x][i];
if(!vis[u]){
dfs(u,x);
}
}
}
int Lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(int i=20;i>=0;i--){
if(dep[y]<=dep[x]-(1<<i)){
x=f[x][i];
}
}
if(x==y) return x;
for(int i=20;i>=0;i--){
if(f[x][i]==f[y][i]) continue;
else{
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
void sol(int now,int lst){
for(int i=0;i<tu[now].size();i++){
int u=tu[now][i];
//if(u==lst) continue;
sol(u,now);
cnt[now]+=cnt[u];
}
}
signed main()
{
//faster();
cin>>n>>k;
for(int i=1;i<=n-1;i++){
int u,v;
cin>>u>>v;
tu[u].push_back(v);
tu[v].push_back(u);
}
dfs(1,0);
for(int i=1;i<=k;i++){
int x,y;
cin>>x>>y;
int mid=Lca(x,y);
cnt[x]++;
cnt[y]++;
cnt[mid]--;
cnt[f[mid][0]]--;
}
sol(1,0);
int ans=-1;
for(int i=1;i<=n;i++){
ans=max(ans,cnt[i]);
}
cout<<ans;
return 0;
}
Day 6
DFS序
定义
对于每个节点，在其第一次被搜索到和回溯时，将其加入答案序列，最终所得序列即为DFS序
如图：
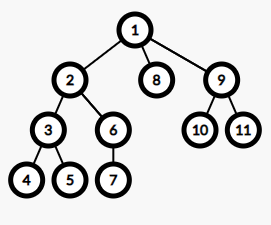
此图DFS序即为1 2 3 4 4 5 5 3 6 7 7 6 2 8 8 9 10 10 11 11 9 1
特点
- 每个节点恰好在这个序列中出现两次
- 记 \(L_i\),\(R_i\) 分别为节点 \(i\) 第一次和最后一次出现的位置，那么 \(L_i-R_i\) 中间那段即为节点 \(i\) 的子树。
时间戳
\(dfn[i]\) 表示节点 \(i\) 在DFS序上第一次出现的位置
换句话说，\(dfn[i]\) 为节点 \(i\) 的时间戳。
例题：
LOJ #144
给定一棵树和上面节点的点权，对这棵树做以下操作
- 将节点 \(i\) 的点权加 \(x\)
- 求出节点 \(a\) 的所有子树的点权之和
Day7
区间DP
状压DP(状态压缩)
- 动态规划设计时需要设计多个状态来转移方程
- 状态太多那么维度就会太多，导致复杂度爆炸
- 那么因此可以将多个状态压缩成一个维度来存储
- 具体看例题
例题:
形式化来说，给定n个点，要求从 \((0,0)\) 出发，求出经过全部 \(n\) 个点的最小距离
- 考虑DP，由于有多个状态，应此考虑状态压缩
- 设 \(dp[i][j]\) 为当前到达第 \(i\) 个点，之前经过 \(j\) 这个二进制数所代表的点之后所得的最小距离(例如 \(dp[3][10]\)代表当前在编号为 \(3\) 的点，之前已经经过 \(1\) , \(3\) 的点(因为\((10)_{10}=(1010)_{2}\) )
- 考虑到 \(n\) 的范围小，由此可以暴力枚举从哪个编号的奶酪去另一个编号的奶酪
- 由此得出方程转移式:
\[dp[i][j]=\min_{k = 1 , k \ne i}^{n}(dp[i][j],dp[k][j-2^{i-1}]+dis(k,i)
\]
- 其中 \(dis(x,y)\) 代表编号为 \(x\) 的奶酪到编号为 \(y\) 的奶酪的距离
- 再添加一些细节...
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=15+5;
int n;
double f[N][(1<<15)+7];
pair<double,double> nl[N];
double dis(int x,int y){
return sqrt((nl[x].first-nl[y].first)*(nl[x].first-nl[y].first)+(nl[x].second-nl[y].second)*(nl[x].second-nl[y].second));
}
signed main()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>nl[i].first>>nl[i].second;
}
nl[0].first=0;
nl[0].second=0;
memset(f,127,sizeof(f));//根据memset通过内存赋值的性质，用memset给f数组赋127代表给double类型赋最大值
double ans=f[0][0];//注意：这里一定不能改为 ans=127,这样就不是double类型的最大值了
for(int i=1;i<=n;i++){
f[i][1<<(i-1)]=dis(0,i);//只经过第i点的点集为(0,0)到第i点的距离
}
for(int i=1;i<(1<<n);i++){
for(int j=1;j<=n;j++){
if((i&(1<<(j-1)))!=0){//若枚举的i点集的第j项不为0，即经过了j这个点
for(int k=1;k<=n;k++){
if((i&(1<<(k-1)))!=0&&j!=k) {//若枚举的i点集的第k项不为0，即经过了k这个点，且现在枚举的第k点与刚才枚举的第j点不相同。
f[i][j]=min(f[i][j],f[k][j-(1<<(i-1))]+dis(i,k));
}
}
}
}
}
for(int i=1;i<=n;i++){
ans=min(ans,f[i][(1<<n)-1]);//枚举终点分别为第i点时的答案 ，从中取最优
}
cout<<fixed<<setprecision(2)<<ans;
return 0;
}
Day8
T1
给定 \(n\) 个点，在这 \(n\) 个点中任意选 \(3\) 个点组成一个三角形，求所有可以组成的三角形中面积为整数的三角形个数
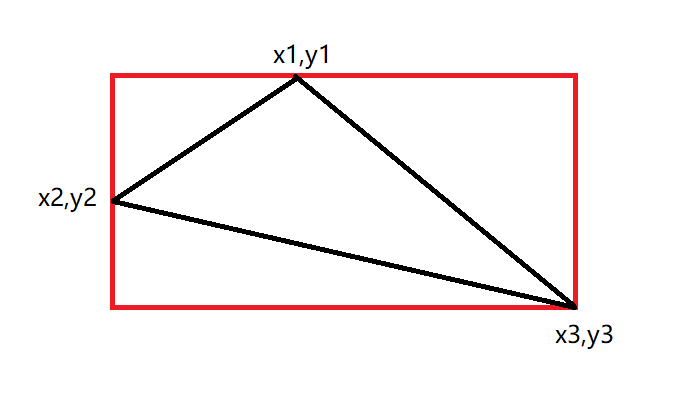
- 如图，对于每个三个点构成的三角形面积可以通过如图方式去在矩形割小三角形面积来求
- 由此可以推出式子
\[\large S_{abc}
=\displaystyle \frac{1}{2}(x_1-x_2)*(y_1-y_2)+\displaystyle \frac{1}{2}(x_3-x_1)*(y_1-y_3)+\displaystyle \frac{1}{2}(x_2-x_3)*(y_3-y_2)
\]
\[=\large \dots
\]
\[=\large \displaystyle \frac{1}{2}(x_1*y_2+x_2*y_3+x_3*y_1-y_3*y_2-x_2*y_1-x_1*y_3)
\]
- 观察公式，发现三角形面积是否为整数只与 \(x_1*y_2+x_2*y_3+x_3*y_1-y_3*y_2-x_2*y_1-x_1*y_3\)
的奇偶性有关 - 进而得知三角形面积是否为整数只与 \(x_i,y_i\) 的奇偶性有关
- 因此可以把不同奇偶性的 \(x_i,y_i\) 替换为 \(0,1\) 求出所有不合法的数量(即那一大坨式子不为2的倍数）
- 再用总数量 \(C_{n}^{3}\)减去不合法方案数，剩下即为合法的方案数量
由于不同奇偶性的xi,yi替换为 0,1 求出所有不合法的数量，这里分类讨论不合法时的情况有点抽象，所以可以再写一个程序求出这些不合法情况。
代码
#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<stack>
#include<stdio.h>
#include<cstring>
#include<math.h>
#include<iomanip>
#include<algorithm>
#define int long long
using namespace std;
const int N=5e4+5;
void faster(){
ios_base::sync_with_stdio(false);
cout.tie(0);
cin.tie(0);
}
int n;
pair<int,int> sa[N];
int sum[3][3];
signed main()
{
//faster();
cin>>n;
for(int i=1;i<=n;i++){
cin>>sa[i].first>>sa[i].second;
int f1=sa[i].first%2;
int f2=sa[i].second%2;
sum[f1][f2]++;//sum[i][j]表示x的奇偶性为i，y的奇偶性为j时的点的总数
}
int ans=n*(n-1)*(n-2)/6;//总方案数
ans-=(sum[0][0]*sum[0][1]*sum[1][0]);
ans-=(sum[0][0]*sum[0][1]*sum[1][1]);
ans-=(sum[0][0]*sum[1][0]*sum[1][1]);
ans-=(sum[0][1]*sum[1][0]*sum[1][1]);
/*
用程序分类讨论了四种不合法情况
0 0
0 1
1 0
0 0
0 1
1 1
0 0
1 0
1 1
0 1
1 0
1 1
*/
cout<<ans;
return 0;
}
Day9
组合数
从 \(n\) 个物品中选 \(k\) 个物品，求所有方案数量为多少
上述问题统称为组合数问题
记 \(C_n^k\) 为所有从 \(n\) 个物品中选 \(k\) 个的方案数，那么就有下述式子：
\[\large C^k_n=\frac{n!}{k!(n-k)!}
\]
\[\large C^k_n=C^{n-k}_{n}
\]
\[\large C^k_n=C^{k-1}_{n-1}+C^{n-1}_{k}
\]
只需要记住这三个即可，这是最重要的。
方格涂色问题：
当前有 \(n\) 个方格,每个方格只能涂上 \([1,m]\) 种颜色。要求每个相邻的方格颜色不一样。
请问总共有多少种方案
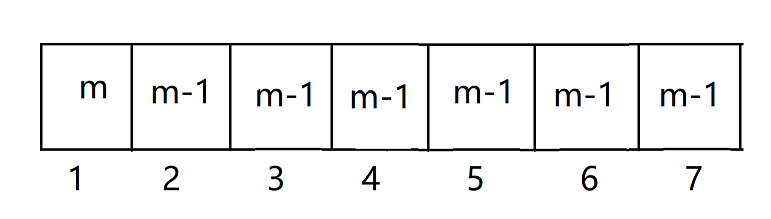
- 如图，第一格的颜色有 \(m\) 种填法，由于不能相邻第二个的颜色共有 \(m-1\) 种填法...以此类推，得到图中所示
- 根据乘法原理，总方案数就为 \(m*(m-1)^{n-1}\) 个
忽略相邻要求影响，易得总方案数为 \(m^n\)，合法方案数为 \(m*(m-1)^{n-1}\) 个。因此用总方案数减去不合法方案数即可
注意到数据范围较大，需要使用快速幂
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
const int mod=100003;
int ans;
int n,m;
int ksm(int a,int b){
if(b==0) return 1;
if(b==1) return a;
int u=ksm(a,b/2)%mod;
u=u%mod*u%mod;
if(b%2==1){
u=u%mod*a%mod;
}
return u%mod;
}
signed main()
{
cin>>m>>n;
int ans=ksm(m,n)-(m%mod)*ksm(m-1,n-1)%mod;
while(ans<0) ans+=mod;
cout<<ans;
return 0;
}
浙公网安备 33010602011771号