哈希重温
重写一下。高清重制版。
字符串哈希（进制哈希/一维哈希）
详解
把字符串通过哈希函数映射成一个哈希值，理想情况下，哈希值相等，字符串也就相等。
下文我们约束字符串为 $str$，长度分别为 $n$，以 $1$ 为起始下标。
类比成 $base$ 进制的理解，有：
$$hash(str)=\sum_{i=1}^{n} str_i \times base^{n-i}$$
利用前缀和的性质，设 $h_i$ 为字符串 $str$ 的前 $i$ 位的哈希值，这样可以高效表示哈希值。
不难得出：$h_i=h_{i-1} \times base + str_i$。可以类似秦九韶公式去理解。
于是，对于 $[L, R]$ 内的哈希值有： $h_R-h_{L-1} \times base^{R-L+1}$。
相当于把进制补齐，因为在算到 $h_R$ 时 $h_{L-1}$ 的哈希值共被累乘了 $base^{R-(L-1)}$。
而现在想得到 $[L, R]$ 内的哈希值，用 $h_R$ 的哈希值直接减去 $h_{L-1}$ 的哈希值时，需要先把 $h_{L-1}$ 的哈希值补回来。
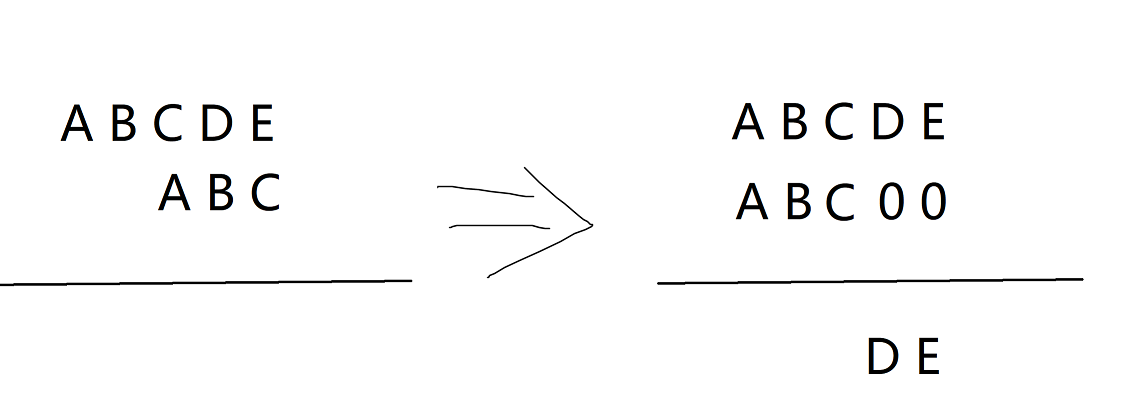
如 $ABCDE - ABC$ 按照正常思维是 $DE$，但如果要取到 $DE$，我们要先补齐 $ABC$，变成 $ABC00$
然后再用 $ABCDE-ABC00=DE$，就像一个竖式，如下图
一些技巧：
1.通常，进制数 $base$ 取 $131$，$13331$ 等等，选这两个数冲突小到几乎无。
2.且需要对哈希值进行取模，数太大会爆。通常模数 $p$ 取一个大质数，不然容易冲突。
可以用自然溢出哈希，不用 $\mod p$，映射出来的数定义成 unsigned long long 类型，会自爆，自动取模。
3.用双哈希，防止被卡，双重保险（自然溢出容易被卡）
这里不同哈希函数，$base$ 不应相同。
例题
板子，先把每个字符串映射成哈希值后，这样就能 $O(1)$ 比较了。
如何比较？直接排序就好了。
P2957 [USACO09OCT] Barn Echoes G（Code）
求一个字符串的前缀和另一个字符串的后缀相等的最长长度。板子。
二维哈希
详解
进制哈希就是一维的，二维也差不多，可以当成很个一维哈希拼在一起。也就是把若干行拼在一起，变成一行。
设 $h_{i,j}$ 表示矩阵的左上角为 $(1,1)$，右下角为 $(i,j)$ 时的哈希值。
类比二维前缀和，也是把进制补齐的方法，可以得到：$h_{i, j}=h_{i-1,j} \times base1 + h_{i,j-1} \times base2 - h_{i-1, j-1} \times base \times base2 + str_{i, j}$。
为了避免冲突，所以要用另一个 $base2$，因为行列的偏移量是不同的。这里对于行是 $base1$，列是 $base2$。
当然可以类似高维前缀和的方法，把行列分开单独处理，更好理解。
先从列开始 $h_{i,j}=h_{i,j-1} \times base2 + a_{i,j}$，再从行开始，则此刻转移为 $h_{i,j}=h_{i-1,j} \times base1 + h_{i,j}$。
获取 $(ax, ay)$ 到 $(bx, by)$ 的哈希值也是同理，进制补齐就好：
$$h_{bx, by} - h_{bx, ay-1} \times base2^{by-ay+1} - h_{ax-1, by} \times base1^{bx-ax+1} + h_{ax-1, ay-1} \times base1^{bx-ax+1} \times base2^{by-ay+1}$$
这里进制补齐的正确性是好证明的，可以把尝试把子矩阵的哈希值用 $a_{i, j}$ 逐个表示出来，然后再类比一维哈希补回来多累乘的值，你发现是可以分配进去的，正确性就是对的。
例题
P10474 [ICPC-Beijing 2011] Matrix 矩阵哈希
求小矩阵是否在大矩阵中出现过。小矩阵和大矩阵的大小固定。
因为大小都是固定的，可以直接预处理。
具体的就是在处理大矩阵 hash 值。在大矩阵中求每个小矩阵的 hash 值，用 map 记录这个值。
再算小矩阵 hash 值，查 map 中是否出现过即可。
就很板了，贴个代码：
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N=1005;
const ull base=131, base2=13331;
char s[N][N];
ull p[N], p2[N];
int n, m, a, b, G;
struct mar
{
int n, m, a[N][N];
ull h[N][N];
void init()
{
for (int i=1; i<=n; i++) for (int j=1; j<=m; j++) h[i][j]=h[i-1][j]*base+h[i][j-1]*base2-h[i-1][j-1]*base*base2+(ull)a[i][j];
}
ull get(int ax, int ay, int bx, int by)
{
return h[bx][by]-h[bx][ay-1]*p2[by-ay+1]-h[ax-1][by]*p[bx-ax+1]+h[ax-1][ay-1]*p[bx-ax+1]*p2[by-ay+1];
}
}A, B;
map<ull, bool> mp;
int main()
{
p[0]=p2[0]=1;
for (int i=1; i<=1000; i++) p[i]=p[i-1]*base, p2[i]=p2[i-1]*base2;
scanf("%d%d%d%d", &n, &m, &a, &b), A.n=n, A.m=m, B.n=a, B.m=b;
for (int i=1; i<=n; i++) scanf("%s", s[i]+1);
for (int i=1; i<=n; i++) for (int j=1; j<=m; j++) A.a[i][j]=s[i][j]-'0';
A.init();
for (int i=1; i+a-1<=n; i++) for (int j=1; j+b-1<=m; j++) mp[A.get(i, j, i+a-1, j+b-1)]=1;
scanf("%d", &G);
while (G--)
{
for (int i=1; i<=a; i++) scanf("%s", s[i]+1);
for (int i=1; i<=a; i++) for (int j=1; j<=b; j++) B.a[i][j]=s[i][j]-'0';
B.init();
printf("%d\n", (int)mp[B.get(1, 1, a, b)]);
}
return 0;
}
树哈希
详解
树哈希是很灵活的，可以设计出各种各样的哈希方式，结合题目具体设计就好。
设节点 $u$ 的哈希值是 $h(u)$，我们当前先讨论不区分不同子树的情况。
因为不区分不同子树，可以用加法，就是可以累加子树的哈希（当然异或应该可以），即定为：
$$h(u)=G\left(\sum_{v\in\text{son}(u)}h(v)\right)$$
这里 $G$ 用于限制 $h$ 的大小，一般是取模。但是如果只有取模则所有哈希值均为零，所以可以改成加上一个常数然后取模。当然用自然溢出则不用考虑取模，加一个常数即可。
但显然，这太容易被卡了，考虑对每个哈希值进行一些变换，如下：
$$h(u)=G\left(\sum_{v\in\text{son}(u)}F(h(v))\right)$$
这里 $F$ 是某一个整数到整数的映射，可以用多项式混合异或+位移（学名叫 xor-shift） 的方法。
任何哈希都必然可以被对着卡掉，为了预防出题人对着 $xor-shift$ 卡，还可以在映射前后异或一个随机常数。这样就很难再被卡了。
具体的，$F$ 的写法如下（参考自 XorShift ）：
mt19937_64 rnd(time(0));
ull rd=rnd();
ull merge(ull x)
{
x^=rd, x^=(x<<5), x^=(x>>11), x^=(x<<54), x^=rd;
return x;
}
如果需要区分不同子树呢？类似进制哈希的就好。把若干个子树的哈希值当成一维哈希里的数。
对于每一个 $u$ 的孩子 $v$，有：
$$h(u)=G\left( h(u) \times base + h(v)\right)$$
这种情况的写法就很多种了，可能比较难写出固定的不被卡的写法。
例题
给出一个 $n$ 个点的有根树，你需要选择若干个子树，使得两两不同构，最大化选择子树数量。
有根树同构的板子。
同构：两棵树同构，当且仅当点数相同，且可以将一棵树重新标号，使得这两棵树完全相同。
这里同构是不考虑子树顺序的，于是按照套路设计哈希函数即可，然后求出所有子树的哈希值。
哈希值相同就是同构，那么用 set 维护不同哈希值的个数，就是不同同构的子树数量。
贴个代码：
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N=1e6+5;
int n, u1, v1;
vector<int> a[N];
mt19937_64 rnd(time(0));
ull mark, mark2, h[N];
set<ull> s;
ull merge(ull x)
{
x^=mark, x^=(x<<5), x^=(x>>11), x^=(x<<54), x^=mark;
return x;
}
void dfs(int u, int fa)
{
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (v==fa) continue;
dfs(v, u);
h[u]+=merge(h[v]);
}
h[u]+=mark2, s.insert(h[u]);
}
int main()
{
mark=rnd(), mark2=rnd();
scanf("%d", &n);
for (int i=1; i<n; i++)
{
scanf("%d%d", &u1, &v1);
a[u1].push_back(v1);
a[v1].push_back(u1);
}
dfs(1, 0);
printf("%d", s.size());
return 0;
}
给定 $m$ 棵无根树，每棵树有一个编号。对于每一棵树，输出最小的与它重构的树的编号。
无根树同构板子。
考虑到我们构造的哈希函数是一个求和的形式，我们可以考虑换根 dp，求出以每一个点为根时的哈希值。
然后你可以钦定所有根哈希值中最大 / 最小的为整棵树的哈希值（如果你愿意，中位数、平均值也行）。
然后用 map 去维护就好了。
另外一种方法是找重心，只需要考虑重心为根的情况就好。
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N=1e6+5;
int G, n, u1;
vector<int> a[N];
mt19937_64 rnd(time(0));
ull mark, mark2, h[N], h2[N], mx=0;
map<ull, int> ans;
ull merge(ull x)
{
x^=mark, x^=(x<<11), x^=(x>>45), x^=(x<<14), x^=mark;
return x;
}
void dfs(int u, int fa)
{
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (v==fa) continue;
dfs(v, u);
h[u]+=merge(h[v]);
}
h[u]+=mark2;
}
void dfs2(int u, int fa)
{
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i];
if (v==fa) continue;
h2[v]=h[v]+merge(h2[u]-merge(h[v]));
dfs2(v, u);
}
h2[u]+=mark2, mx=max(mx, h2[u]);
}
int main()
{
mark=rnd(), mark2=rnd();
scanf("%d", &G);
for (int T=1; T<=G; T++)
{
for (int i=1; i<=n; i++) a[i].clear(), h[i]=h2[i]=mx=0;
scanf("%d", &n);
for (int i=1; i<=n; i++)
{
scanf("%d", &u1);
if (!u1) continue;
a[i].push_back(u1);
a[u1].push_back(i);
}
dfs(1, 0);
h2[1]=h[1];
dfs2(1, 0);
if (ans[mx]) printf("%d\n", ans[mx]);
else ans[mx]=T, printf("%d\n", T);
}
return 0;
}
这题需要考虑子树的顺序。先鸽着吧。
不需要考虑子树顺序，咕咕咕：
SP7826 TREEISO - Tree Isomorphism
异或哈希
详解
异或哈希利用了异或操作的特殊性和哈希降低冲突的原理，处理一类 ”一个序列的排列组合是否在另一个序列出现“ 的问题。
因为是排列组合，是不考虑顺序的，刚好可以用上异或，但是单纯用异或冲突概率极大，便用上哈希降低冲突。
具体的，思考这样一个问题：给定长度为 $n$ 的序列 $a$ 和 $b$，判断能否让序列 $a$ 的某个排列等于序列 $b$。
发现是不关心顺序的，恰好异或有交换律，于是判断 $a_1 \oplus a_2 \oplus ... \oplus a_n = b_1 \oplus b_2 \oplus ... \oplus b_n$ 是否成立即可。
但显然这样是错的，因为不同数异或结果容易冲突。考虑用哈希把每个数映射成一个很大的数，这样冲突概率就很小了。
也就是考虑构造好了映射函数 $f$，然后就变成判断 $f(a_1) \oplus f(a_2) \oplus ... \oplus f(a_n) = f(b_1) \oplus f(b_2) \oplus ... \oplus f(b_n)$ 是否成立即可。
例题
CF1175F The Number of Subpermutations
先把原 $a$ 序列用哈希映射成大数，这样就可以 $O(1)$ 判断一个区间的排列是否为 $1$ 到 $r-l+1$ 了。
暴力枚举区间还是 $O(n^2)$ 的，考虑观察性质降低复杂度。
观察到：合法区间一定包含 $1$，且其最大值就是区间长度。
于是从 $1$ 的位置左右扩展即可。复杂度降至 $O(n)$
参考
浙公网安备 33010602011771号