线段树进阶

请确保您有一定的线段树基础中的基础。至少确保了解过并会实现模板题。

如果您的基础不太好，可以先看完基础内容部分。

本文部分链接无法打开，见谅！（其实本文应该也看不到的。但是我想着留篇遗产挂在 blog 上就没隐藏了）

线段树基础

基础操作包含：

1.基础的区间操作（修改+查询）

2.基础的单点操作（修改+查询）

3.维护一段连续的值（如最大子段和）

4.多个 lazy_tag 的操作

分析一些不易理解的地方。

1.线段树基础操作的复杂度为什么是 logn

单点操作显然正确。考虑区间操作即可。

观察到，线段树每层区间是连续的。区间操作的区间也是连续的。

当查询到某层时，中间部分一定会被包含，仅仅是左右两端的部分没被包含。

倘若中间部分被包含，那么在当前层之前一定会被访问到并停下。

所以每次只有两端会继续往下遍历。每次会往左右儿子遍历。然后一共 logn 层。所以最坏是 4logn 的复杂度。

2.线段树为什么开 4 倍空间

设 $d_i$ 表示度为 $i$ 的点的个数。

显然：$2d_2+d_1+1=d_2+d_1+d_0$，线段树是完全二叉树，无度为 1 的节点。

那么有 $d_2=d_0-1$，设线段树维护区间长度为 $n$，则 $d_0=n$。那么线段树有 $2n-1$ 个点。

在操作时可能访问最后一个点的左右儿子，即最大访问到 $2(2n-1)+1=4n-1$，那么开 4 倍空间即可。

3.多个懒标记如何下放

一些基本理解：多个懒标记即多种操作，一个 lazy_tag 只是考虑维护一种操作的总和，且 lazy_tag 是直接对数操作的。

举个例：加乘标记，例如操作是 +a*b+c，那么 add=a+c, mul=b，假设该数是 x，对该数进行先乘后加的懒标记操作后变为 x*b+(a+c)。

但实际结果应该为 (x+a)*b+c

考虑了某种下放顺序，但这样会有影响（如上面那个例子），消除影响，即可正确维护。

如何消除影响？在做出某种操作时直接修改标记。

举个例：在出现乘法操作时，对于先前的加法操作修改，使得之后的懒标记对数字直接修改是正确的。

出现 *b 时，让 add*b，即 add=a*b，那么最终 add=a*b+c, mul=b，对该数进行先乘后加的懒标记操作后变为 x*b+(a*b+c)。容易发现和实际结果一样。

如何一般化？考虑把多种懒标记融合在一个 push_down，一起下放，我们定优先级就能确定下放顺序了，顺便消除影响。

此时分离开 push_down 和一起 push_down 效果一样。因为没影响标记。只是标记下放的早晚罢了。

举个例：覆盖+翻转操作（后面的例题，P2572 [SCOI2010] 序列操作）

我们定覆盖优先级更高。先下放覆盖。

如果原序列操作顺序是：先覆盖，后翻转，由于我们定了覆盖优先级更高，一定会保证先覆盖，把覆盖标记也下放之后，然后翻转，是没问题的。

如果原序列操作顺序是：先翻转，后覆盖，由于我们定了覆盖优先级更高，会先覆盖，且下放覆盖标记。

但其实应该先翻转，不过注意到无论如何翻转最终一定会被覆盖，就可以直接清空翻转标记，这样也是正确的。

放线段树上，此操作对于该结点是这样的，对于该结点的儿子结点也是一样。

1）每次有覆盖操作，需把先前的翻转操作清空。这点体现在 push_down 和 upd_cover 中。

对于 push_down 的理解：当前节点都覆盖，清空翻转标记了，把当前节点两个子节点的翻转标记肯定也要清空了。

2）由于每次操作都会顺路 push_down，保证了在翻转之前的覆盖标记，在下传时不会把该翻转标记清掉，因为此时的翻转标记还没打上。是先下放完后再打上的。

void upd_cover()
{
	if (qL<=L && R<=qR)
	{
		push_down_rev();
		...
	}
	push_down();
}


void upd_cover()
{
	if (qL<=L && R<=qR)
	{
		...
	}
	push_down();
}

即以上两种写法一样。可以直接选择后者。

这是两种操作。如果三种操作呢？就比较复杂了，例如 P10639 吉司机线段树

先鸽着。

4.多种标记如何下放的技巧

把 push_down 当做二元组下放，如 (a, b) 下放到 (a2, b2)，考虑先乘后加。那么就是 (a2, b2) = (a2b+a, b2b)。

5.对于维护左右前缀一类线段树的理解

1.在维护左右前缀时，没有合并条件可以考虑直接合并。取最优。因为不影响。

2.在区间查询时，有合并两颗线段树的操作，这启发我们只要信息能够合并（交换律+结合律），都可以考虑线段树维护。

线段树例题

都是基础操作，但是比较有意思的题。

推式子

对于一类奇怪/不方便维护的式子，不妨先做些转换，推推式子再做。

P1471，Code

展开方差公式，并重新推导，变成一个优美的容易维护的式子。

P10463，Code

考虑弱化版。单点修改，是容易维护的。我们把区间修改转为单点修改，就是差分一下。

但是差分数组的 gcd 是原数组的 gcd 吗？推式子证明发现可行。

码农题

P2572，Code

操作是容易维护的。但是码农。

这里给出写线段树的技巧：压行，减少没必要的代码。但是不要破坏代码的可读性。具体可以参考下此题代码。

思维题

P3582，Code

仍然是先考虑弱化版，如果没有每个数只能取一次的限制就是最大子段和了。

然后再升级回强化版，有每个数取一次的限制呢？我们可以破除这个限制。

具体的，选择在每次遇到第一个前面出现过的元素，就把前面那个的贡献改为 -1，然后前面第二个出现的贡献改为 0。也就是支持单点修改

这样做也有问题：修改后再想在前面统计的答案是错误的。因此，我们继续消除影响，在每次修改贡献之前都更新一次答案，这样就避免了这种问题。

SP2916，Code

本题容易想到，先分讨区间无交集，是方便统计答案的。有交集呢？应该枚举中间断点，然后统计答案。但复杂度接受不了。

分类讨论的本质：正常需要枚举才能统计答案。但是发现枚举出来的结果有一些共性，我们可以对有相同共性的结果统一起来求，避免了枚举的复杂度。

分类讨论还要关注分讨的对象，如何分讨，全不全面。

于是分讨最大子段和的左右端点，会穿过哪些区间。然后就容易做了。

杂(水)题

P5522，Code

发现维护的字符串只有 3 个字符，相当于三进制。我们可以把三进制拆成 2 个二进制。然后就容易维护了。这样极大节省了空间与码量。

P4344，Code

水题。操作 2 可以转化成区间覆盖，但是如何确定覆盖长度？发现有单调性，二分就好。

线段树的扩展

列举一些线段树常见的扩展应用。

先弄这么多吧，还有很多鸽子之后补。

鸽子链接：https://www.luogu.com.cn/paste/p3vt7lbk

动态开点线段树

普通线段树是预先把所有点的编号分配好，即左儿子两倍，右儿子两倍加一编号方法。然后用堆式存储。通过 build 函数对结点的值初始化。

当线段树数量太多（线段树合并）或下标值域太大（权值线段树）时，由于空间限制，无法使用预先分配好所有点的编号。

解决方法是动态开点：即动态的对点分配编号。对于需要用到的结点，再创建出来对其初始化，不需要用的点就不创建。

当然也可以离散化，而且一般离散化空间可能优于动态开点，不过前提是能离线下来。

例题

具体用例题引入：CF915E Physical Education Lessons

题意很简单，维护区间覆盖即可，不过范围很大，需要动态开点线段树。

我们动态对点进行分配编号即可，但是正因如此，每个结点左右儿子也是不确定的。所以对于每个结点，需要维护其左右儿子的编号。

在向下递归时，若当前结点为空则新建结点。所以在询问操作时，遇到没有创建的结点，就可以直接返回了。可以类比 Trie 理解。

一般通过传递引用的方式快速更新子结点编号。

基本和正常线段树是一样的，不过改变了对儿子的编号方式。然后由于动态开点，就不需要 build 函数了。

一些细节：

1.注意在 push_down 时，如果没有儿子结点，需要先创建出来。不然值更新时会错。

2.需要额外记录线段树的根 rt，因为是传递引用更新编号，所以得传个变量进去。

具体可看代码：Submission #350679963 - Codeforces，不过注意要卡常卡空间。

开点过程，挂张图理解：

假如需要维护区间 [1, 4]，我们需要修改 [3,3]。（图中灰色的部分表示没有开点的部分）

第一步（在根节点rt）：

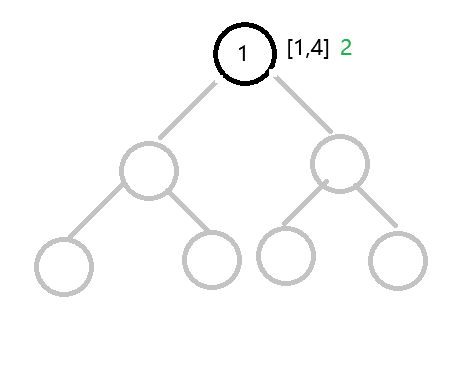
因为根节点是第一个遍历的节点，所以创一个根节点，编号为 1。

第二步（遍历到表示[3,4]节点）：

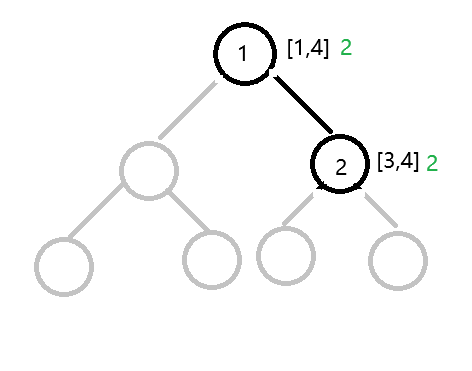
因为这个节点是第二个遍历的节点，所以创出该节点，编号为 2。

第三步（遍历到表示[3,3]的叶子节点）：

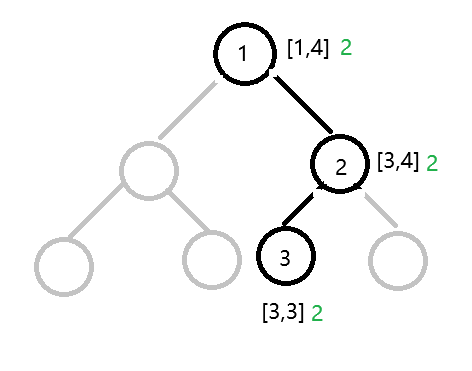
因为这个节点是第三个遍历的节点，所以创出该节点，编号为 3。

空间复杂度

根据线段树的原理，每次操作最多遍历到 4logn 个结点，其余很多结点是没用的，而动态开点线段树我们只关心用到的结点数量，即最多创建 4qlogV 个节点。

所以一般开的开到 4qlogV 就足够了，但是如果碰到卡空间的题怎么办？进一步分析下。

发现每次操作，只有没创建的点才会创建出来，所以每次操作并不一定创建 4logn 个结点。

线段树从第 0 层开始算，不妨设前 B 层都铺满结点，后 (logV-B) 层挂了若干条链。

那么总结点数就是：2^(B+1)+4q(logV-B)。

然后对于 B，可以随便取，看题目 q，V 的范围而定取到最小值即可。通常取 logq 就可以。

带进去算就是：2q+4q(logV-logq)。一般开到这个空间是最优了，而且也够用了。

如果普通线段树被卡空间了，我换成动态开点线段树，也是可以省空间的，因为线段树最多 2n-1 个点，开满也就 2n-1 个点。所以这里开 2n 就够用了。

练习

P13825 【模板】线段树 1.5（Code）

维护区间加，区间和的动态开点线段树，本质一样。

不过需要解决一个问题，刚开始每个点初始值该怎么处理？

正常线段树是通过 build 处理，动态开点呢？那就在创建出该节点时，初始化就好了。因为我们只关心用到的结点，所以只需要对用到的点初始化。

所以在询问操作时，遇到没有创建的结点，也需要创建出来，并对其初始化。所以也需要传递引用。

这里需要注意：每次都需要把当前点的儿子节点给创建出来并初始化，不然在 push_up 的时候会合并错误。

这一点在 push_down 中实现就好，push_down 不管当前点是否有标记，都要把没创建的儿子创建出来。

CF803G（Code）

和上题一样，需要在创建出一个点的时候，对这个点初始化。

那如何初始化？用 ST 表，然后类似分块思想去做就行了。

标记永久化

众所周知，有区修就考虑 push_down，所以要存懒标记并且及时下放。

但部分线段树下传懒标记的代价过大，或不支持下传懒标记。

例如扫描线维护的覆盖次数+覆盖长度，就没有 push_down 操作。如果下放了覆盖次数，之后再取消覆盖是难维护的。于是考虑挂到当前节点不下放就好。

说到扫描线，这又启发我们，线段树维护的东西不一定是点，可以是线段。就如之后的扫描线，李超线段树。只不过侧重点在于，你想要什么维护什么为基础单位。

又例如可持久化线段树和动态开点线段树，下传懒标记需要新建结点，空间常数大。

又例如树套树，无法下传懒标记。

此时可以用标记永久化的技巧：按着懒标记不下传，查询时，考虑从根到当前区间的路径上每个点的懒标记对当前点的影响就好。

于是标记永久化有卡常的作用，还可以省去 push_down，代码会简单很多。

以动态开点的练习题 P13825 【模板】线段树 1.5 讲解。

题目要求区间加，区间查。

每个区间要维护两个值，add 表示当前点的懒标记。sum 表示不考虑当前点的所有祖先节点的 add 标记时的区间和。

注意，这里 sum 是需要考虑自身懒标记的，但不考虑祖先的懒标记。以及 add 是仅考虑当前区间的懒标记情况，不考虑任何祖先。

区间加时，把沿路节点的 sum 都更改就好，这里为什么不先改完后回溯用 push_up 更新，而是沿路往下遍历的时候就直接算贡献呢？

因为在动态开点时，会利用 push_down，把当前点的儿子节点创出来，确保 push_up 合并时值的正确性，现在没了 push_down，用 push_up 合并时值可能出错。

于是只能沿路往下更新。如果还是选择创建儿子并 push_up 的方法，标记永久化的优势就体现不出来了。

区间查时，需要把沿路的 add 标记统计起来，代表祖先节点对当前点的影响，也即大区间对小区间的影响。然后把这个影响给统计上就可以了。

具体可以看代码：Code

我们探究什么样的 “信息-标记” 二元组可标记永久化。

在查询过程中，我们按照从根到当前区间的顺序合并懒标记信息，与这些标记被打上的时刻顺序不同。

例如三次修改

在原线段树的基础上满足这个条件，就可以用标记永久化做区间修改，区间查询了。

有交换律一定可以做，但没交换律是否就不可做了呢？可以用一些技巧。如记录时间戳等等。具体参考下面给出的链接。

更多操作下的标记永久化可参考：标记永久化

线段树二分

全局二分

咕咕咕。

区间二分

咕咕咕。

值域线段树（权值线段树）

顾名思义就是维护值域的线段树，专门维护值的某种信息，比如维护值的出现次数，可以理解为维护一个桶。

其实跟正常线段树没区别，就是按照值域开空间而已。

值域通常比较大，需要和动态开点相结合。就是针对值域维护的是一颗动态开点线段树。

然后就可以实现平衡树的各种操作。P3369 【模板】普通平衡树，具体如下：

这里假设值域是 [1, V]。

1.插入/删除一个数 x，就是在对应值域 x 处加一或减一，代表出现次数加一或减一，即单点修改。

2.查询第一个 x 的排名，就是查询 [1, x-1] 值域的数字总出现个数 sum，x 的排名就是 sum+1。即区间查询。

3.查询最后一个 x 的排名，就是查询 [1, x] 值域的数字总出现个数 sum，x 的排名就是 sum。即区间查询。

4.查询排名为 k 的数，就是线段树全局二分。左子树维护的值域数字总出现个数比 >= k，就往左子树内找答案，否则往右子树内找答案。直到找到一个叶子节点停下。

5.查询 x 的前驱，先找 x 的排名 k（第一个 x 的排名），再找排名为 k-1 的数即可。

6.查询 x 的后继，先找 x 的排名 k（最后一个 x 的排名），再找排名为 k+1 的数即可。

加强版也可以过：P6136 【模板】普通平衡树（数据加强版）（Code）

扫描线基础

扫描线板子：扫描线（就是基于线段树的离线化算法）

一些理解：

1.线段树里到底存线段还是节点

看情况。比如维护面积并/周长并，需要合并两线段长度，所以以点为单位不好合并，以线段为单位就好维护（单位=叶子节点）

每个叶节点相当于存了 [L, R) 的线段，合并起来直接相加就好，很方便。

一些细节：

1.扫描线在排序时，一定要考虑在 x 坐标重合时，对操作先后顺序有排序。具体看题目而定。
2.因为存的是左右两个线段，所以注意空间开 2 倍。

扫描线例题

巧妙转化题

P1502，Code

转换一下，考虑星星能被哪些窗口框住。

注意，研究对象应该统一，如本题研究框住星星的窗口，是以星星为原点，窗口在星星的右上角，对象都是统一一个方向，右上角。而不能上下左右四个方向，不然无法求解。

所以维护一个最大值的扫描线即可。

以下 3 题可以直接看：[扫描线] 数据结构测试(2025.3.22)

CF377D，Gym 308768F，CF997E（第 3 题先鸽子）

吉司机线段树基础

咕咕咕。打算补一点

吉司机线段树例题