相遇(容斥+最短路+分类,水紫)
给定一个有n个节点m条边的无向图,在某一时刻节点st上有一个动点a, 节点end上有一个动点b, 动点a向节点end方向移动,要求是尽快到达end点,与此同时,动点b向节点st方向移动,要求是尽快到达st点, 但是整个过程中a和b不能相遇,问两点不相遇一共有多少种方案。
不相遇是指在同一时刻两点都不在同一节点或同一边上。结果可能很大,对1e9+7取模
输入格式
第一行两个整数n和m
第二行两个整数st和end
接下来m行,每行三个整数u,v,t, 表示u和v有一条长为t的边
其中1<=n<=1e5, 1<=m<=2e5,1<=t<=1e9
数据不存在重边和自环
输出格式
一个整数
输入/输出例子1
输入:
4 4
1 3
1 2 1
2 3 1
3 4 1
4 1 1
输出:
2
样例解释
无
直接求不相遇比较难,用减法原理。
很容易想到,首先要搞一个最短路计数。
dis[i]:s->i最短路,cnt[i]:s->i的最短路路径数
dis2[i]:t->i最短路,cnt2[i]:t->i的最短路路径数
用全部方案-相遇方案,就是答案
全部方案:最短路径条数平方。也就是 cnt[t]*cnt[t](cnt2[s]*cnt2[s] 也行)
相遇是在节点上相遇或者边上相遇
分别算就好
判断能否在u节点相遇:
枚举每个点,看看能否在点上相遇
条件:看看dis[s->u]是否等于dis[t->u],且s-u + t-u 是最短路
贡献:(cnt[u]*cnt2[u])^2
计算如下:
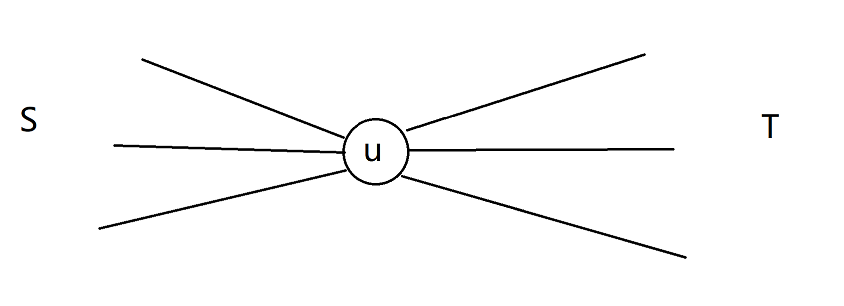
假设s到u有3条路可以走,t到u也有3条路可以走
那么我们可以考虑让s走第1条,走到t可以分别走3条。
我们还可以考虑让s走第2条,走到t可以分别走3条。
我们还可以考虑让s走第3条,走到t可以分别走3条。
所以就是 cnt[u]*cnt2[u]
但是我们还可以反过来,从t走,走到s
那么我们可以考虑让t走第1条,走到s可以分别走3条。
我们还可以考虑让t走第2条,走到s可以分别走3条。
我们还可以考虑让t走第3条,走到s可以分别走3条。
所以就是 cnt[u]*cnt2[u]
那么答案就是这俩相乘。
边上相遇:
枚举每条边,是否会在那条边相遇。
条件:这条边在最短路上。 s-u+w+t-v 是最短路
还有两个条件:
dis[s->u]+w>dis[t->v]
dis[s->v]+w>dis[t->u]
这里第二个条件类似第一个条件,就是u,v换了下而已。
举个例看看:

比如:u->v,也就是 w=3,v->t=6,也就是dis[v->t]=6
如果dis[s->u]是3,就或在6这个地方相遇,也就是v号点。(也就是说dis[s->u]+w = dis[v-t]是不行的)
那如果此时调整一下dis[s->u],我们减小一下,改成dis[s->u]是2,会在5.5这个地方相遇,那么这个时候会超过v (也就是说dis[s->u]+w<dis[v-t]是不行的)
再改,dis[s->u]是4,会在6.5这个地方相遇,刚好在v里面。(也就是说 dis[s->u]+w>dis[v-t]是可行的)
也就是说,一个人走过这条边之前,另一个人必须至少走上这条边。
贡献:(cnt[s-u]*cnt[t-v])^2
和计算点的贡献是一样的。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=200005, Mod=1e9+7;
struct node
{
int v, w;
bool operator <(const node &A) const
{
return w>A.w;
};
};
struct node2
{
int u, v, w;
}ask[N];
int n, m, s, t, u1, v1, w1;
int dis[N], vis[N], cnt[N], dis2[N], vis2[N], cnt2[N], ans=0, sum=0;
vector<node> a[N];
priority_queue<node> q, q2;
void dij()
{
memset(dis, 63, sizeof dis);
memset(vis, 0, sizeof vis);
dis[s]=0, cnt[s]=1;
q.push({s, 0});
while (!q.empty())
{
int u=q.top().v;
q.pop();
if (vis[u]) continue;
vis[u]=1;
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i].v, w=a[u][i].w;
if (dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
q.push({v, dis[v]});
cnt[v]=cnt[u]%Mod;
}
else if (dis[v]==dis[u]+w) cnt[v]=(cnt[v]+cnt[u])%Mod;
}
}
}
void dij2()
{
memset(dis2, 63, sizeof dis2);
memset(vis2, 0, sizeof vis2);
dis2[t]=0, cnt2[t]=1;
q2.push({t, 0});
while (!q2.empty())
{
int u=q2.top().v;
q2.pop();
if (vis2[u]) continue;
vis2[u]=1;
for (int i=0; i<a[u].size(); i++)
{
int v=a[u][i].v, w=a[u][i].w;
if (dis2[v]>dis2[u]+w)
{
dis2[v]=dis2[u]+w;
q2.push({v, dis2[v]});
cnt2[v]=cnt2[u]%Mod;
}
else if (dis2[v]==dis2[u]+w) cnt2[v]=(cnt2[v]+cnt2[u])%Mod;
}
}
}
signed main()
{
scanf("%d%d%d%d", &n, &m, &s, &t);
for (int i=1; i<=m; i++)
{
scanf("%d%d%lld", &u1, &v1, &w1);
a[u1].push_back({v1, w1});
a[v1].push_back({u1, w1});
ask[i]={u1, v1, w1};
}
dij();
dij2();
sum=dis[t];
ans=cnt[t]*cnt[t];
for (int i=1; i<=n; i++)
if (dis[i]==dis2[i] && dis[i]+dis2[i]==sum) ans=((ans-(cnt[i]*cnt[i]%Mod*cnt2[i]%Mod*cnt2[i]%Mod))+Mod)%Mod;
//printf("%lld\n", ans%Mod);
for (int i=1; i<=m; i++)
{
int u=ask[i].u, v=ask[i].v, w=ask[i].w;
if (dis[u]+w+dis2[v]==sum && dis[u]+w>dis2[v] && dis2[v]+w>dis[u]) ans=((ans-cnt[u]*cnt[u]%Mod*cnt2[v]%Mod*cnt2[v]%Mod)+Mod)%Mod;
swap(u, v);
if (dis[u]+w+dis2[v]==sum && dis[u]+w>dis2[v] && dis2[v]+w>dis[u]) ans=((ans-cnt[u]*cnt[u]%Mod*cnt2[v]%Mod*cnt2[v]%Mod)+Mod)%Mod;
}
printf("%lld", ans%Mod);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号