半回文串（dp套dp）

第4题     半回文串 查看测评数据信息

给定一个长度为n的只含小写英文字母的字符串S和一个整数k,请你将S分成k个子字符串，使得每个子字符串变成半回文串需要修改的字符数目最少。请你返回一个整数，表示需要修改的最少字符数目。

下面定义什么事半回文串：如果一个字符串从左往右和从右往左读是一样的，那么它是一个回文串。如果长度为len的字符串存在一个满足1<=d<len的正整数d,1en%d=0成立且所有对d做除法余数相同的下标对应的字符连起来得到的字符串都是回文串，那么我们说这个字符串是半回文串。比方说"aa"，"aba","adbgad"和"abab"都是半回文串，而”a”，"ab"和"abca"不是。子字符串指的是一个字符串中一段连续的字符序列。

输入格式

 

第一行一个长度是n的字符串S

第二行一个整数k

2<=n<=200,1<=k<=n/2

 

输出格式

 

一个整数

 

输入/输出例子1

输入：

abcac

2

 

输出：

1

 

样例解释

 我们可以将S分成子字符串"ab"和"cac"。子字符串"cac"已经是半回文串。如果我们将"ab"变成"aa",它也会变成个d=1的半回文串。该方案是将S分成2个子字符串的前提下，得到2个半回文子字符串需要的最少修改次数。所以答案为1。

 

dp套dp是什么

---

做题目先搞第一个dp，但是光凭第一个dp可能搞不完，中间再用第二个dp预处理一些值，再继续第一个dp继续做。

第二个dp可能是线性的等等的。

又或者说是先预处理一个dp，然后再进行第二个dp。

反正不是真正意义上的dp“套”dp

 

这题咋做

---

做法1

f(i, j) 表示枚举到第i位，j表示枚举的这个字符串的头部在哪，头是j，尾是i，也就是字符串中的j~i

对于每个字符串，枚举约数，变成很多段，每一段用贪心求出变成回文串次数，总次数就出来了，然后取一个总最小次数，也就是整个字符串最小次数

这里跟做法2差不多，没做法1的代码和详解，我们直接看做法2

 

 

做法2
直接把一串字符串变成k个半回文很难搞，用大局观。

f(i, j): 当前考虑到第i个字符，恰好划分成j段，且这j段字符串都是半回文串，所花费的最小操作次数。
转移：
这一段肯定由前面一段转移，然后累加当前花费的操作次数对吧。

但是我们要知道这一段的字符串具体是什么，才能累加当前贡献。所以我们得枚举k，才知道这一段从哪开始，然后这一段的字符串就是k~i了

f(i, j)=f(k-1, j-1)+(k~i)这一段变成半回文的花费

例如：

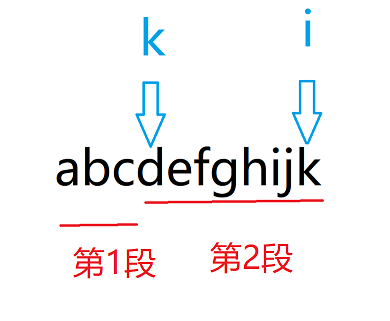
 第2段肯定由第1段转移过来嘛。然后考虑前i个字母，假设当前枚举的k是第4位，那么当前这一段的字符串不就是k~i吗，那么前一段的字符串就是1~k-1

也就是 f(i, 2)=f(k-1, 1)+(k~i)变成半回文的花费

 

这里计算 f 就是 O(n^3)

 

所以现在考虑预处理 k~i 变成半回文的花费

我们定 g(i, j)，表示 i到j这一段字符变成半回文需要花费

那么根据题意模拟即可。

先枚举因数，对于每一个因数，我们可以拼接成len/d个字符串（len是字符串长度，d是因数），然后我们计算把每个字符串变成回文串需要修改的最小次数的总和，然后再统计一下答案的min值，因为只要一个因数满足条件就行。

把字符串变成回文串的最小修改次数怎么求？也是简单模拟+贪心即可。

如果字符串首尾不同，那么改首位任意一个的字母即可，所以修改次数就要+1

 

这里计算 g 就是 O(n^2*sqrt(n))，这样一看复杂度肯定不会超时的嘛

 

 f的初始化，就是f[0][0]=0，也就是前0个字母，第0段，不需要修改就满足条件。

答案就是f[n][k]，f的前n个字母，分成k段嘛。

#include <bits/stdc++.h>
using namespace std;
const int N=205, M=105;

char s[N], a[N];
vector<int> v;
int p, n;
long long g[N][N], f[N][M];
long long solve(int L, int R)
{
	int len=R-L+1;
	
	v.clear();
	for (int i=1; i*i<=len; i++)
		if (len%i==0)
		{
			v.push_back(i);
			if (i!=1) v.push_back(len/i);
		} 
	
	int cnt=0;
	long long res=1e9, res2=0;
	for (int i=0; i<v.size(); i++)
	{
		//printf("{%d}", v[i]);
		for (int k=0; k<v[i]; k++)
		{
			for (int j=L+k; j<=R; j+=v[i]) a[++cnt]=s[j];
		/*	for (int j=1; j<=cnt; j++) printf("%c ", a[j]);
			puts("");*/
			
			for (int j=1; j<=(cnt+1)/2; j++) if (a[j]!=a[cnt-j+1]) res2++;
			
			cnt=0;
		}
		res=min(res, res2);
		res2=0;
	}
	
	return res;
}
int main()
{
	scanf("%s", s+1);
	n=strlen(s+1);
	
	scanf("%d", &p);
	
	for (int i=1; i<=n; i++)
		for (int j=i; j<=n; j++)
			g[i][j]=solve(i, j);
	/*
	for (int i=1; i<=n; i++)
	{
		for (int j=i+1; j<=n; j++)
			printf("g[%d][%d]=%d ", i, j, g[i][j]);
		puts("");
	}
	*/
	memset(f, 63, sizeof f);
	f[0][0]=0;
	for (int i=1; i<=n; i++)
		for (int j=1; j<=p; j++)
			for (int k=1; k<i; k++)
				f[i][j]=min(f[i][j], f[k-1][j-1]+g[k][i]);
	
	printf("%lld", f[n][p]);
	return 0; 
}