矩阵前k次幂之和（矩阵套矩阵的技巧）

第1题     矩阵前k次幂之和 查看测评数据信息

给出一个n*n的矩阵A，求A^1 + A^2 + A^3 + ... + A^k。

输入格式

 

第一行，两个整数，n和k。 1<=n<=30,  1<=k<=1000000000。

接下来是n行n列的矩阵A。

 

输出格式

 

输出最后的矩阵，每个元素都是模1000000007。

 

输入/输出例子1

输入：

2 2

0 1

1 1

 

输出：

1 2

2 3

 

样例解释

无

 

方法一
假设我们要求  A^1+A^2+A^3+A^4+A^5+A^6
但是可以发现  A^4+A^5+A^6=A^3(A^1+A^2+A^3)
所以折半，记忆化搜索
dfs(6)=dfs(3)*A^3 即可

 

方法二

考虑动态规划
f[k] : A^1+A^2+A^3+....+A^k
f[k]=f[k-1]+A^K

 

那现在可以构造矩阵了

[f(k-1), A^k] * [未知矩阵] = [ f(k), A^(k+1) ]

矩阵中的矩阵
由于f，A都是矩阵
所以未知矩阵中的矩阵全都是矩阵

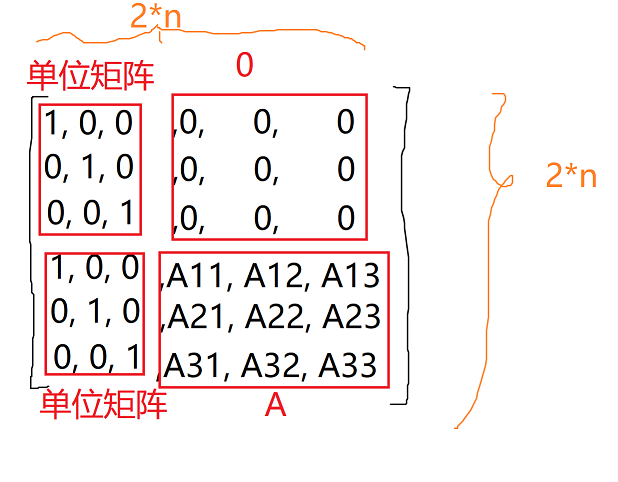
[未知矩阵]:
[单位矩阵， 0]
[单位矩阵， A]

 

但是注意，不要傻傻的真的写了矩阵套矩阵，可以把矩阵拆解出来，每个矩阵当成一堆数字就好了

具体地：

假设n=3（也就是A矩阵是3*3大小的，那么此时f矩阵肯定也是3*3大小的）

当k=1时：

已知矩阵 [f(k-1), A^k] 可以转换成：（注意，因为此时k=1，所以A^k=a[i][j]，也就是输入的矩阵的数据，这里图中的Aij=a[i][j]）

 

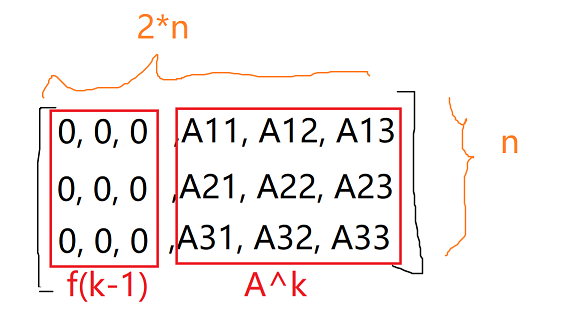
 那么[未知矩阵] 也可以转换一下：

 

目标矩阵就不画了，跟已知矩阵差不多了，答案就很显然了，直接打印求得的目标矩阵的i：1~n，j：1~n的数据即可

 

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=105, Mod=1000000007;

struct mp
{
	int n, m;
	int a[N][N];
	
	void init(int row, int col, bool isI)
	{
		n=row, m=col;
		memset(a, 0, sizeof a);
		
		if (isI)
			for (int i=1; i<=row; i++) a[i][i]=1;
	}	
}A, B, T;
mp operator * (const mp A, const mp B)
{
	mp C;
	C.init(A.n, B.m, 0);
	for (int i=1; i<=A.n; i++)
		for (int j=1; j<=B.m; j++)
			for (int k=1; k<=A.m; k++)
				C.a[i][j]=(C.a[i][j]+A.a[i][k]*B.a[k][j])%Mod;
		
	return C;
}
mp qpow_mp(mp A, int k)
{
	mp res;
	res.init(A.n, A.m, 1);
	while (k>0)
	{
		if (k&1) res=res*A;
		A=A*A;
		k>>=1;
	}
	
	return res;
}
int n, k;
signed main()
{
	scanf("%lld%lld", &n, &k);
	B.init(2*n, 2*n, 0);
	T.init(n, n, 0);
	
	for (int i=1; i<=n; i++)
		for (int j=1; j<=n; j++)
		{
			scanf("%lld", &T.a[i][j]);
			B.a[n+i][n+j]=T.a[i][j];
		}
			
	
	for (int i=1; i<=n; i++)
		B.a[i][i]=1, B.a[n+i][i]=1;
	
	A.init(n, 2*n, 0);
	for (int i=1; i<=n; i++)
		for (int j=1; j<=n; j++)
			A.a[i][n+j]=T.a[i][j];
	
	A=A*qpow_mp(B, k);
	
	for (int i=1; i<=n; i++)
	{
		for (int j=1; j<=n; j++)
			printf("%lld ", A.a[i][j]);
		printf("\n");
	}
		
	return 0;
}