迷宫（bfs，关键是此题模数）

第3题     迷宫 查看测评数据信息

给一个n×m矩阵迷官c[n][m]，第i行第j列的值为c[i][j],机器人jqr在迷宫中迷路了需要帮助。机器人jqr当前在(1,1)的位置，出口在(n,m),这个迷言有一个计数器，只有当计数器的值模(p-1)的余数为0时迷宫出口才会开门(出口没有开门意味着即使在(n，m)的位置也不能逃出去）。机器人jqr每一秒会向迷言的上下左右四个方向走一步（不可以不走），并且不能走出迷言的边界，假设机器人jqr从(x,y)走到了(p,q),然后计数器将会加上c[p][q],特别的，计数器初始是c[1][1]。

现在有两个二维数组a[n][m]和b[n][m]。其中。问机器人jqr最快多久可以走出迷宫。

输入格式

 

第一行三个整数n,m,p(1<=n,m<=10,2<=p<=1e4)

接下来n行m列，表示a[i][j]

接下来n行m列表示b[i][j]

其中0<=a[i][j],b[i][j]<=1e6

 

输出格式

 

一个整数，表示最少需要的步数，如果不可能走出迷宫，输出-1

 

输入/输出例子1

输入：

3 3 10

1 2 3

0 1 4

0 0 0

1 0 0

0 0 1

0 1 0

 

输出：

6

 

样例解释

 

 

 

1.处理c数组
2.f[i][j][k] 机器人走到(i, j)，计数器存的数是k（已经模了p-1），花费的最小步数
3.dp

 

 

这题有个意思的地方，就是模数：

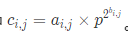
 这个数最终要%(p-1)，那么这个式子最后一个项（p^2^b[i][j]）是否没用呢？

我们把p^2^b[i][j]拆开来看，我们令 n = 2^b[i][j]，即求p^n 能否被 (p-1) 模尽

(p^n) % （p-1）=(p^n-1)   %   (p-1)   *   (p)   %  (p-1)，我们关注最后一项p，被 (p-1)模后余1，带入原式  c[i][j]=a[i][j]*p^2^b[i][j]，我们发现这个1就是没用的，因为是乘法运算

(p^n-1)   %   (p-1)  =   (p^n-2)    %   (p-1)    *   (p)    %    (p-1)。同理，最后一项p没用

........................我们一直不断往下这样处理

[p^n-(n-1)]    %    (p-1)    =    (p^n-(n-1)-1)    %    (p-1)    *    p    %    (p-1)    =    (p^0)    %    (p-1)    *    p    %    (p-1)，由于p^0=1，那么模(p-1)还是余1，最后一项同上面计算，没用，那么，这个式子就是没用的

 

1.bfs中，如果要连续到一个点多次，那么就记忆化，相当于dp了！

2.关注题目中的很奇怪的模数，考虑去化简

#include <bits/stdc++.h>
using namespace std;
const int N=15, M=1e4+5;

struct node
{
	int x, y;
	long long sum;
};
int dx[]={-1, 0, 0, 1}, dy[]={0, -1, 1, 0};
int n, m, p, vis[N][N];
long long a[N][N], b[N][N], c[N][N], f[N][N][M];
queue<node> q;
void bfs()
{
	memset(f, 63, sizeof f);
	f[1][1][a[1][1]]=0;
	
	q.push({1, 1, a[1][1]});
	while (!q.empty())
	{
		int x=q.front().x, y=q.front().y;
		long long sum=q.front().sum;
		q.pop();
		
		for (int i=0; i<4; i++)
		{
			int nx=x+dx[i], ny=y+dy[i];
			if (nx>=1 && nx<=n && ny>=1 && ny<=m)
			{
				int tmp=(sum+a[nx][ny])%(p-1);
				if (f[nx][ny][tmp]>f[x][y][sum]+1)
				{
					f[nx][ny][tmp]=f[x][y][sum]+1;
					q.push({nx, ny, tmp});
				}
			}
		}
	}
}
int main()
{
	scanf("%d%d%d", &n, &m, &p);
	
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++)
			scanf("%lld", &a[i][j]);
	
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++)
			scanf("%lld", &b[i][j]);
	
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++)
			c[i][j]=a[i][j]%(p-1);
	
	bfs();
	
	if (f[n][m][0]==f[0][0][0]) printf("-1");
	else printf("%lld", f[n][m][0]);
	return 0;
}