前缀和(有意思的求区间值思想,重要思想!)
给一个有一个长度为n的数组a[1,2,...n]。
数组a的前缀和定义为s[i]=a[1]+a[2]+...+a[i](对于所有的1<=i<=n),规定s[0]=0
数组a的前缀和前缀最大值为max[i]=max(s[0],s[1],s[2],...s[i])(对于所有的0<=i<=n)
数组a的1类和谐度为为max[i]中不同的元素数量。
数组a的2类和谐度为所有a的所有排列中1类和谐度的种类数。
现在有一个长度为n的数组b[1,2,...n]。
给出q个询问,每个询问包含两个整数l,r,求b[l],b[l+1],b[l+2],...b[r]的2类和谐度为多少。
输入格式
第一行输入一个整数n(1<=n<=1e5),表示序列b的长度。
第二行输入n个整数b[i](1≤|b[i]|≤100).
接着输入一个整数q(1≤q≤1e5),表示询问次数。
然后q行,每行两个整数l,r(1≤l≤r≤n)。
部分数据n<=10
部分数据n<=100
输出格式
共q行,每行一个整数
输入/输出例子1
输入:
5
2 3 -1 -2 4
1
2 4
输出:
2
输入/输出例子2
输入:
10
1 2 5 -5 6 3 -1 6 3 -1
10
1 5
1 3
2 5
3 6
1 10
2 6
6 8
1 7
1 1
2 3
输出:
3
1
2
2
4
3
1
4
1
1
样例解释
对于样例一,序列为[3,-1,2]。
其共六种排列,其1类和谐度有两种,分别为1和2,所以2类和谐度为2
题意
题意有点难懂,化简一下:
给一个区间,求这个区间的不同最大前缀和个数,然后对区间进行排列组合,继续上述操作,进行完这次操作后,求出每个区间排列后的结果,求有多少个不同的结果
例如:
下图a是原数组,共有2个排列组合方法
s[i]为a数组的前缀和,其中s[0]=0
Max[i]为s的前i个数的最大值,即这个区间的不同最大前缀和
第一个区间排列方法的不同最大前缀和的个数为2,记这个2为ans1,分别是{1,3},
第二个区间的不同最大前缀和的个数为2,,记这个2为ans2,分别是{2,3}
我们把答案加入集合,即 {ans1, ans2},发现就是 {2, 2},那么就是1种结果
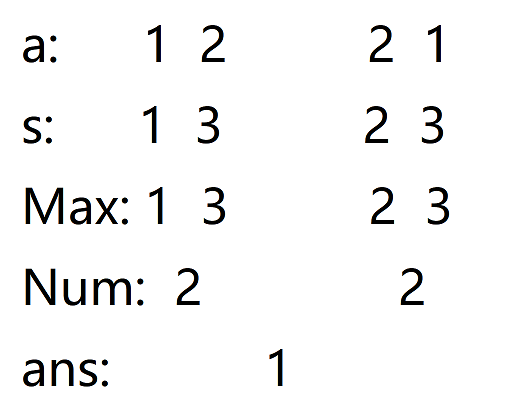
做法
这里先引入一个结论,接下来会证明
求某种属性的种类数: 分别求答案上限,答案下限,上限-下限+1即为所求
那么对于这一题,我们要求出 Max 的上限,下限,那么我们求的不同的结果就是上限-下限+1
求上限
上限,我们想要求出尽量大的不同最大前缀和个数,我们还可以发现一个很直观的规律
如果一个区间的所有数字都>0(不会出现=0的情况,题目有说),那么这个区间的前缀和是一定是单调递增的,Max值也是单调递增的
所以这种情况下,Max不同的数量一定是最多的
但是如果区间中有负数呢?例如此图,代表Max数值大小走向
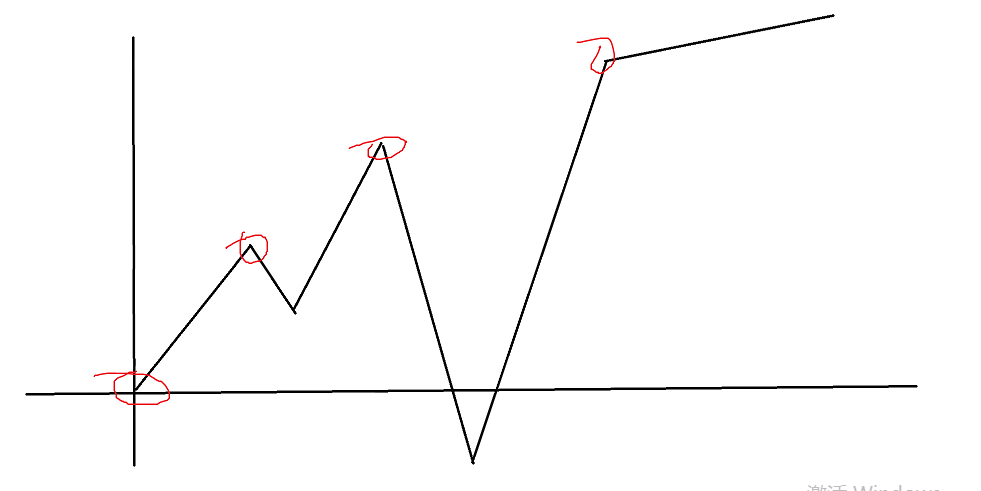
红色圈的数量就是此区间不同Max值的数量,我们发现,如果有一个负数在一个正数的后面,那么这个正数后面的一段区间的Max值都可能是同一个值
我们想要红色圈最多,那么就让这条线不断上升,即Max不断增加,正数用完了,就只能用负数了,会出现一个骤降,就相当于把所有负数安排在这个区间的最后一个正数后面,那么此时不同Max值最多
这里没有严谨证明,但是可以感性理解,如下图
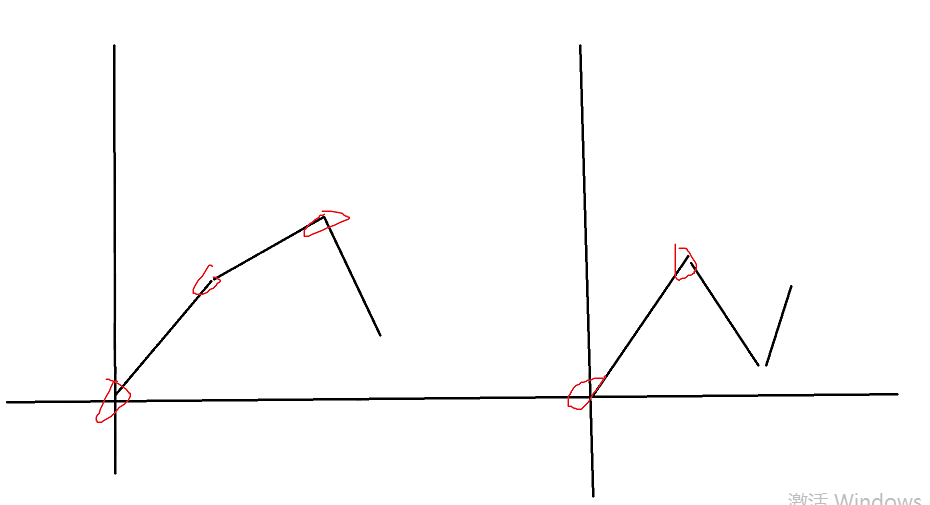
Max如果在中途减小了一个值,那么可能会上升不到原来的高度,那么就不如先在原来的高度上升后,再减少
上限的思路类似于贪心,思路:
正数在最前,负数在最后
ans:所有正数+1
因为Max[0]=0, 0也算一个ans,所以最后要+1
求下限
下限,我们想要求出尽量小的不同最大前缀和个数,那么可以由上限的一个小证明推出来:
Max如果在中途减小了一个值,那么可能会上升不到原来的高度,那么就不如先在原来的高度上升后,再减少
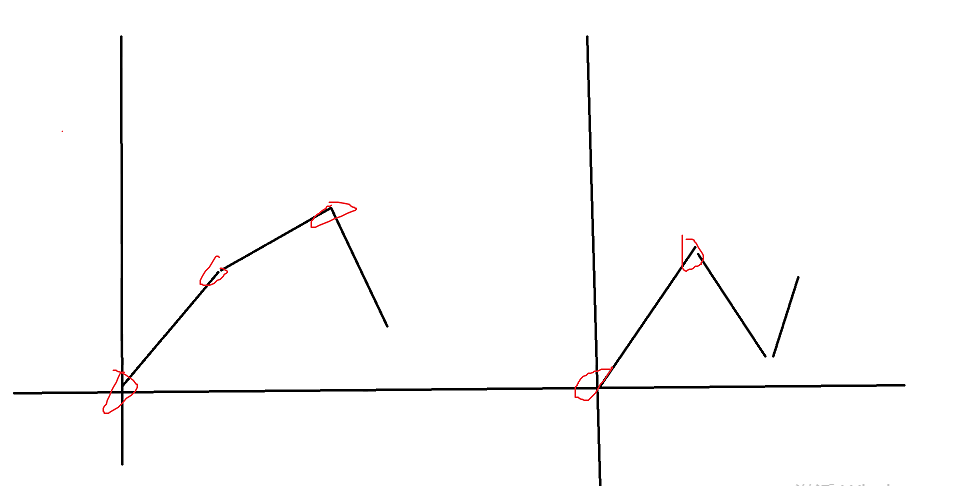
那么我们考虑一会上升,一会下降
那么我们不就是想要下降的值大于上升的值吗?这样先上升,再下降,再上升的时候就回不到原来高度了
所以思路就出来了
用负数尽可能多的抵消正数,这里的抵消也是有要求的,要求最多,所以是把整个负数的值累加,然后把正数从小到大去抵消,这样才能最多
如果还有正数无法被抵消,那么就只能算进答案了
所以,ans:剩余正数+1
为什么加1?同上限,Max[0]=0, 0也算一个答案
证明:在答案上下限中,中间的数是否合法?
为什么开头的结论一定是正确的?
由于作者是蒟蒻,不会严谨的证明,所以......我们构造一组数组看看
一个数列:1 2 -5 1 5 2
上限:6
下限:3
我们看看中间数,4是可以取到的,如下图
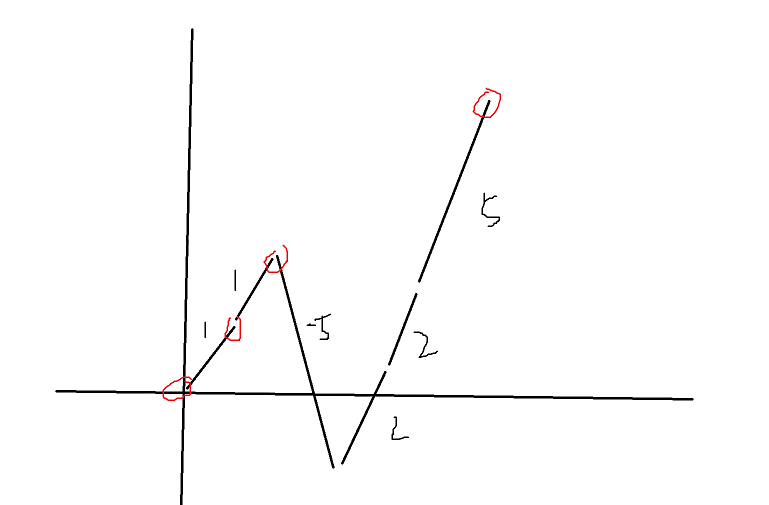
我们看看中间数,5是可以取到的,如下图

好了,那么就证明完毕(比较简陋,哈哈哈)
Code
懂了思路代码是很简单的,不需要注释了,但是根据此题,本代码复杂度错误,是O(nq)的,会超时,好像是用莫队做,蒟蒻较菜,就只会这种做法了,比较也AC了,卡过去了
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n, b[N], tmp[N], q, L, R, Max=0, Min=0, sum=0, cnt=0;
int main()
{
scanf("%d", &n);
for (int i=1; i<=n; i++) scanf("%d", &b[i]);
scanf("%d", &q);
while (q--)
{
Max=0, Min=0, sum=0, cnt=0;
scanf("%d%d", &L, &R);
for (int i=L; i<=R; i++)
{
if (b[i]<0) sum+=b[i];
else if (b[i]>0) Max++;
tmp[++cnt]=b[i];
}
sort(tmp+1, tmp+1+cnt);
for (int i=1; i<=cnt; i++)
{
if (tmp[i]<=0) continue;
sum+=tmp[i];
if (sum>=0)
{
if (sum==0) Min=cnt-i;
else Min=cnt-i+1;
break;
}
}
Max++, Min++;
printf("%d\n", Max-Min+1);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号