次短路问题（最短路）

https://www.luogu.com.cn/problem/P1491

---

第5题     次短路问题 查看测评数据信息

平面直角坐标系中有n个点，m条边，第i个点的坐标是（x[i],y[i]）,求编号为1的点到编号为n的点第二最短路线的距离（保留两位小数），如果存在多条第一短路径，则答案就是第一最短路径的长度；数据没有重边，可能有自环

输入格式

 

第一行两个数n和m

接下来n行，每行两个整数x[i],y[i]

接下来m行，每行两个整数u,v，表示u和v之间有一条路径

其中1<=n<=200,1<=m<=10000, -500<=x[i],y[i]<=500

 

输出格式

 

一行一个数（保留两位小数）

 

输入/输出例子1

输入：

3 3

0 0

1 1

0 2

1 2

1 3

2 3

 

输出：

2.83

 

样例解释

无

 

一般用删边法，这里采用枚举法

我们想求次短路，也就是在跑最短路的过程中加上一条边呗，转换成以下式子：

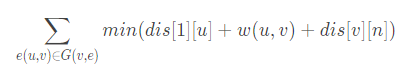
 从1到u的距离我们在第一次跑最短路的时候可以求，v到n的距离可以从n跑一遍然后求一遍，u到v的距离就单纯枚举边

注意，如果有多条最短路，得输出最短路，可以在第一次跑的时候最短路计数

#include <bits/stdc++.h>
using namespace std;
const int N=205;

struct node
{
	int v;
	double w;
	bool operator <(const node &A) const
	{
		return w>A.w;
	};
};
struct node2
{
	int u, v;
	double w;
};
int n, m, x[N], y[N], u1, v1, cnt[N], vis[N];
double dis[N], dis2[N], ans=1e9;
vector<node> a[N];
vector<node2> s;
priority_queue<node> q;
double js(int u1, int v1)
{
	double a=abs(x[u1]*1.0-x[v1]*1.0)*1.0;
	double b=abs(y[u1]*1.0-y[v1]*1.0)*1.0;
	return sqrt(a*a+b*b)*1.0;
}
void dij(int s)
{
	for (int i=0; i<=N-5; i++) dis[i]=1e9;
	memset(vis, 0, sizeof vis);
	memset(cnt, 0, sizeof cnt);
	
	dis[s]=0;
	q.push({s, 0});
	
	while (!q.empty())
	{
		int u=q.top().v;
		q.pop();
		
		if (vis[u]) continue;
		vis[u]=1;
		
		for (int i=0; i<a[u].size(); i++)
		{
			int v=a[u][i].v;
			double w=a[u][i].w;
			
			if (dis[v]==dis[u]+w) cnt[v]++;
			if (dis[v]>dis[u]+w)
			{
				cnt[v]=1;
				dis[v]=dis[u]+w;
				q.push({v, dis[v]});
			}
		}
	}
}
int main()
{
	scanf("%d%d", &n, &m);
	for (int i=1; i<=n; i++) scanf("%d%d", &x[i], &y[i]);
	for (int i=1; i<=m; i++)
	{
		scanf("%d%d", &u1, &v1);
		s.push_back({u1, v1, js(u1, v1)});
		a[u1].push_back({v1, js(u1, v1)});
		a[v1].push_back({u1, js(u1, v1)});	
	}
	
	dij(1);
	if (cnt[n]>1) 
	{
		printf("%.2lf", dis[n]);
		return 0;
	}
	
	for (int i=1; i<=n; i++) dis2[i]=dis[i];
	dij(n);
	
	for (int i=0; i<s.size(); i++)
	{
		int u=s[i].u, v=s[i].v;
		double w=s[i].w;
		
		if(dis2[u]+w+dis[v]>dis2[n]) ans=min(ans, dis2[u]+w+dis[v]); //记得加上判断！不是最短路才行，这里卡了我好久
	}
	
	printf("%.2lf", ans);
	return 0;
}
/*
3 3
0 0
1 1
0 2
1 2
1 3
2 3
*/