空间转移（dp+倍增+Floyd）

第2题     空间转移 查看测评数据信息

给定一个n个点，m条边的有向图，编号从1到n,所有边权值是1，现在有一个动点从点1开始一动，其每秒钟可以移动 2的k次方千米（k 是任意自然数，且2的k次方不超过1000000000）。最少需要几秒才能到达n号点。数据保证 1 到 n至少有一条路径。n⩽50，m⩽10000

输入格式

 

第一行两个整数 n,m，表示点的个数和边的个数。

接下来 m行每行两个数字 u,v，表示一条 u 到 v 的边。

 

输出格式

 

一行一个数字，表示到公司的最少秒数。

 

输入/输出例子1

输入：

4 4

1 1

1 2

2 3

3 4

 

输出：

1

 

样例解释

无

 

 

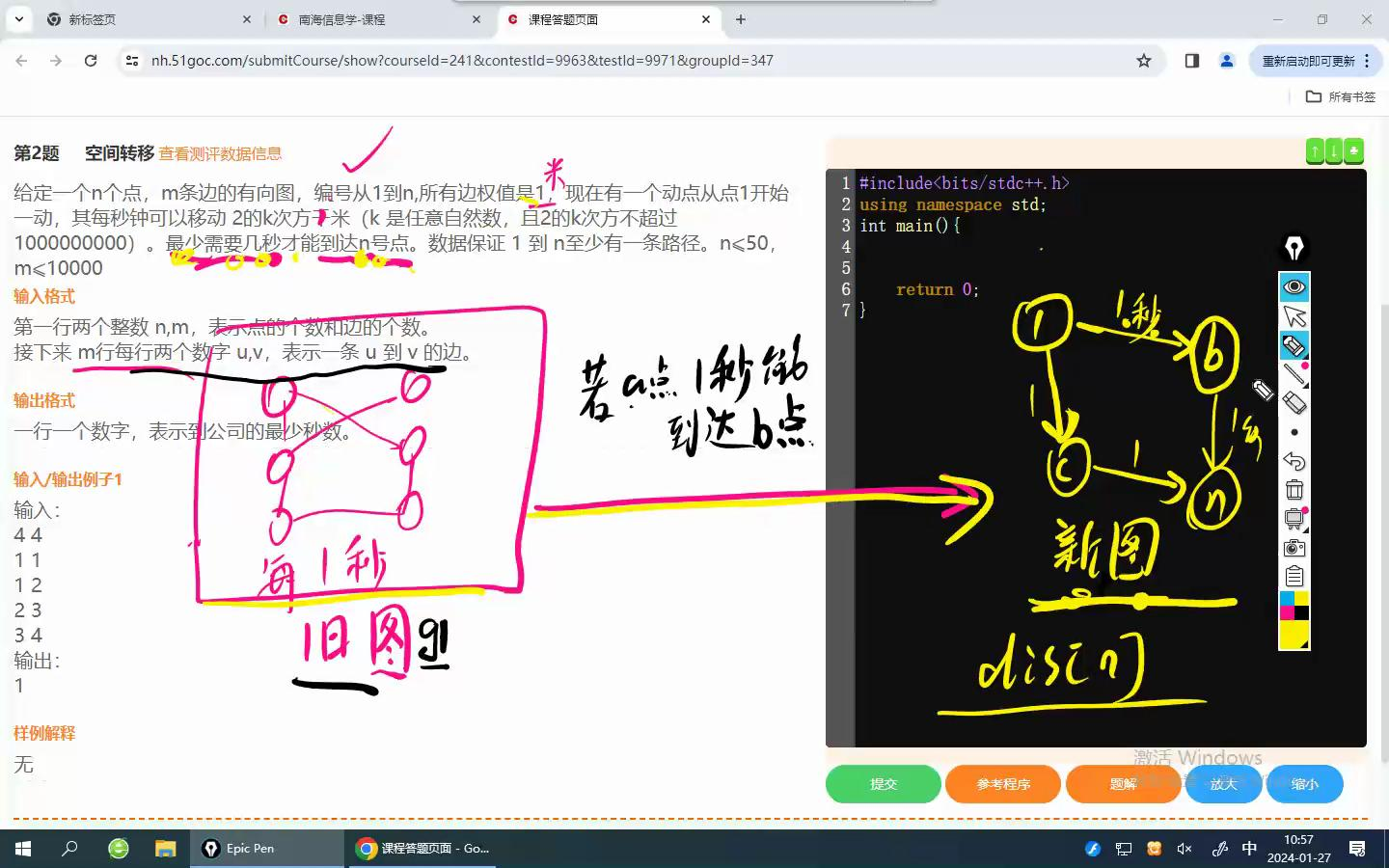
 首先建一个新图，把2的k次方千米能到的点连一条边权为1的路，再跑一遍最短路即可

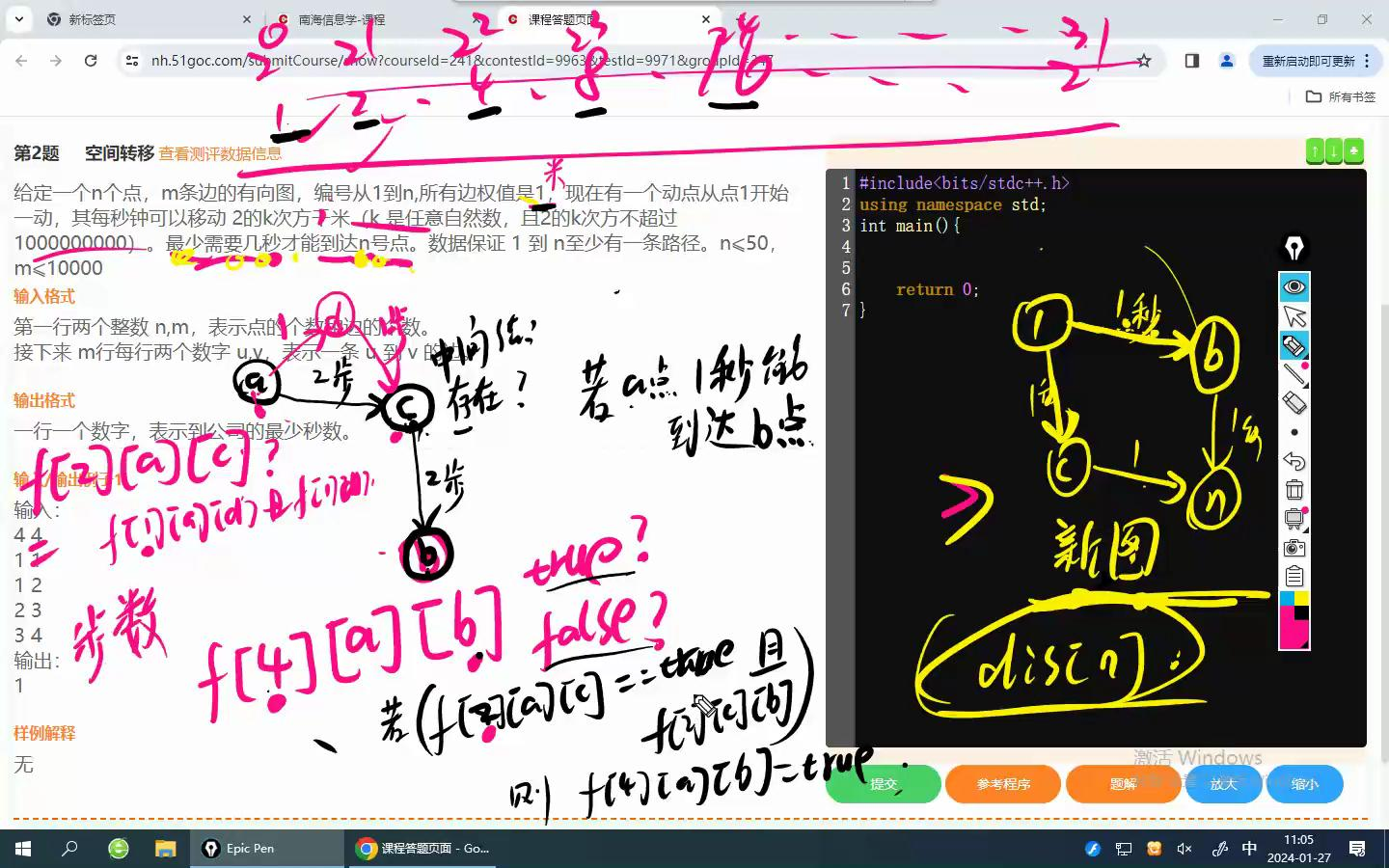
但是我们怎么知道2的k次方千米能到的点呢？

 我们找一个中间点c，看看ac一步走到，cb也可以一步走到，那么a，b就可以一步走到

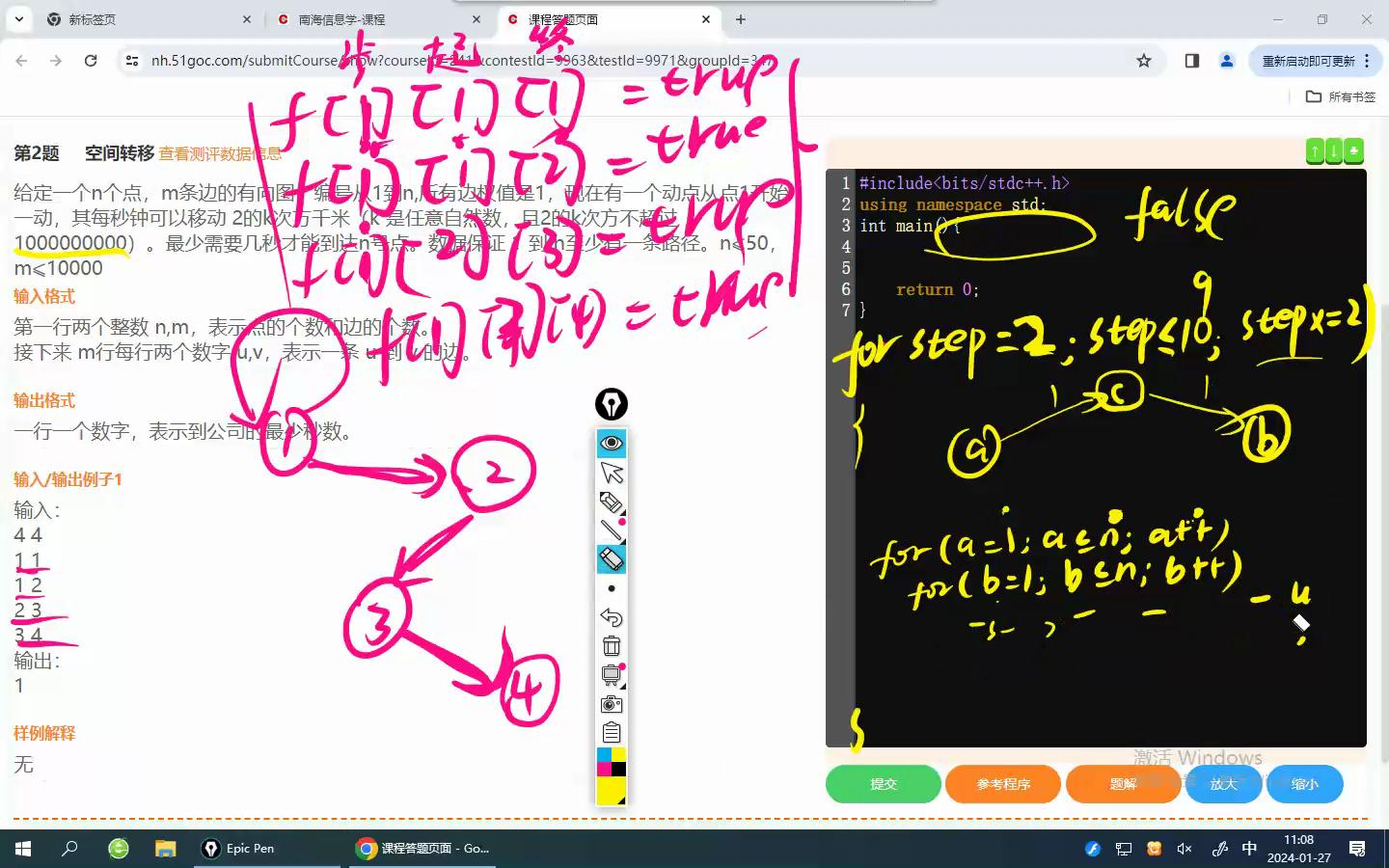
所以我们要记录一下走的状况，f[步数][a][b]=1/0，表示是否能1步走到

#include <bits/stdc++.h>
using namespace std;

const int N=55, M=65;
int n, m, u1, v1, f[N][N][M], dis[N][N]; 
int main() 
{
	memset(f, 0, sizeof f);
	memset(dis, 63, sizeof dis);
	
	scanf("%d%d", &n, &m);
	for (int i=1; i<=m; i++)
	{
		scanf("%d%d", &u1, &v1);
		f[u1][v1][0]=1;
		dis[u1][v1]=1;
	}
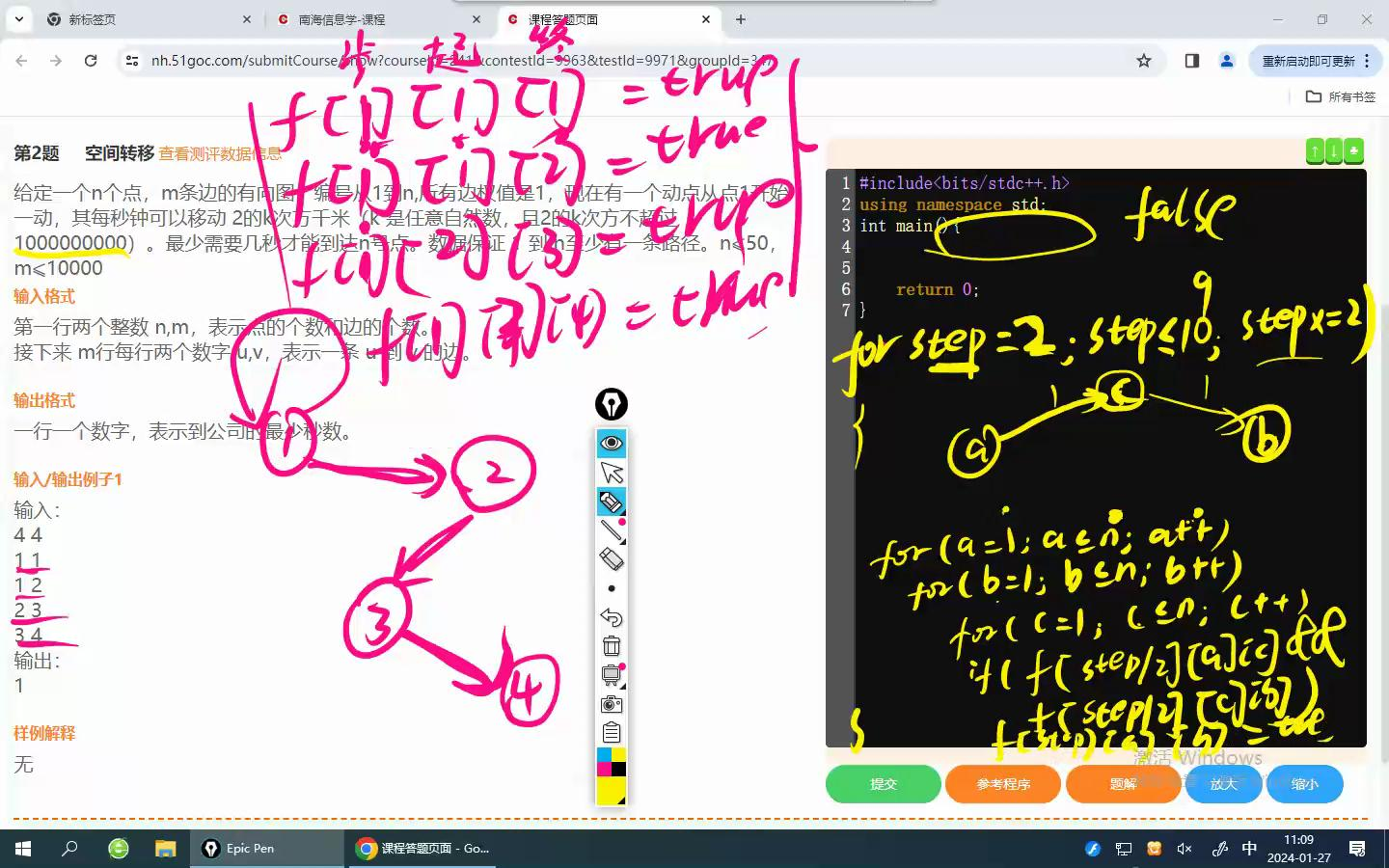
	for (int op=1; op<=64; op++)
		for (int k=1; k<=n; k++)
			for (int i=1; i<=n; i++)
				for (int j=1; j<=n; j++)
					if (f[i][k][op-1] && f[k][j][op-1])
					{
						f[i][j][op]=1;
						dis[i][j]=1;
					}
	
	for (int k=1; k<=n; k++)
		for (int i=1; i<=n; i++)
			for (int j=1; j<=n; j++)
				if (dis[i][j]>dis[i][k]+dis[k][j])
					dis[i][j]=dis[i][k]+dis[k][j];
	
	printf("%d", dis[1][n]);
	return 0;
}

　　

 

附之前的截图