基础数据结构笔记
知识点
链表与邻接表:树与图的存储
单链表

画个图就很好理解了
例题
826. 单链表acwing——826. 单链表_awcing 826-CSDN博客
实现一个单链表,链表初始为空,支持三种操作:
(1) 向链表头插入一个数;
(2) 删除第k个插入的数后面的数;
(3) 在第k个插入的数后插入一个数
现在要对该链表进行M次操作,进行完所有操作后,从头到尾输出整个链表。
注意:题目中第k个插入的数并不是指当前链表的第k个数。例如操作过程中一共插入了n个数,则按照插入的时间顺序,这n个数依次为:第1个插入的数,第2个插入的数,…第n个插入的数。
输入格式
第一行包含整数M,表示操作次数。
接下来M行,每行包含一个操作命令,操作命令可能为以下几种:
(1) “H x”,表示向链表头插入一个数x。
(2) “D k”,表示删除第k个输入的数后面的数(当k为0时,表示删除头结点)。
(3) “I k x”,表示在第k个输入的数后面插入一个数x(此操作中k均大于0)。
输出格式
共一行,将整个链表从头到尾输出。
数据范围
1≤M≤100000
所有操作保证合法。
输入样例:
10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6
输出样例:
6 4 6 5
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int m, k, x;
char op;
//init初始化
int head=-1, e[N], ne[N], idx=1;
// head 表示头结点的下标
// e[i] 表示结点i的值
// ne[i] 表示结点i的next指针是多少
// idx 存储当前已经用到了哪个点
// 将x插入到头结点
void add_to_head(int x)
{
e[idx]=x, ne[idx]=head, head=idx, idx++;
}
// 将下标是k后面的点删掉
void erase(int k)
{
ne[k]=ne[ne[k]];
}
// 将x插入到下标为k的后面
void add(int k, int x)
{
e[idx]=x, ne[idx]=ne[k], ne[k]=idx, idx++;
}
int main()
{
scanf("%d", &m);
while (m--)
{
cin>>op;
if (op=='H')
{
scanf("%d", &x);
add_to_head(x);
}
else if (op=='D')
{
scanf("%d", &k);
if (k==0) head=ne[head];
else erase(k);
}
else
{
scanf("%d%d", &k, &x);
add(k, x);
}
}
for (int i=head; i!=-1; i=ne[i]) printf("%d ", e[i]);
return 0;
}
双链表
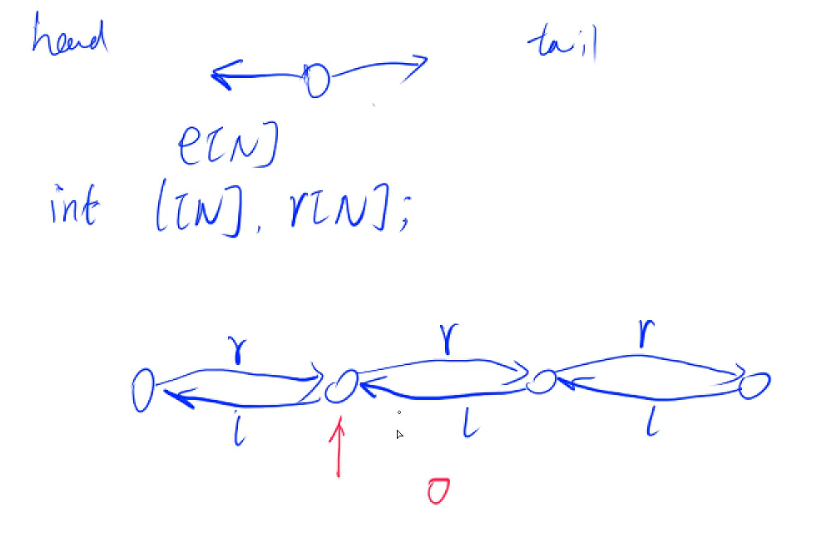
题目来源:AcWing 827. 双链表
一、题目描述
实现一个双链表,双链表初始为空,支持 5 55 种操作:
在最左侧插入一个数;
在最右侧插入一个数;
将第 k kk 个插入的数删除;
在第 k kk 个插入的数左侧插入一个数;
在第 k kk 个插入的数右侧插入一个数
现在要对该链表进行 M MM 次操作,进行完所有操作后,从左到右输出整个链表。
注意:题目中第 k kk 个插入的数并不是指当前链表的第 k kk 个数。例如操作过程中一共插入了 n nn 个数,则按照插入的时间顺序,这 n nn 个数依次为:第 1 11 个插入的数,第 2 22 个插入的数,…第 n nn 个插入的数。
输入格式
第一行包含整数 M MM,表示操作次数。
接下来 M MM 行,每行包含一个操作命令,操作命令可能为以下几种:
L x,表示在链表的最左端插入数 x xx。
R x,表示在链表的最右端插入数 x xx。
D k,表示将第 k kk 个插入的数删除。
IL k x,表示在第 k kk 个插入的数左侧插入一个数。
IR k x,表示在第 k kk 个插入的数右侧插入一个数。
输出格式
共一行,将整个链表从左到右输出。
数据范围
1 ≤ M ≤ 100000 1≤M≤1000001≤M≤100000
所有操作保证合法。
输入样例:
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2
1
2
3
4
5
6
7
8
9
10
11
输出样例:
8 7 7 3 2 9
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int m, k, x;
string op;
int e[N], l[N], r[N], idx=0;
void init()
{
l[1]=0, r[0]=1;
idx=2;
}
void add(int k, int x)
{
e[idx]=x, l[idx]=k, r[idx]=r[k];
l[r[k]]=idx, r[k]=idx, idx++;
}
void erase(int k)
{
r[l[k]]=r[k];
l[r[k]]=l[k];
}
int main()
{
init();
scanf("%d", &m);
while (m--)
{
cin>>op;
if (op=="L")
{
scanf("%d", &x);
add(0, x);
}
else if (op=="R")
{
scanf("%d", &x);
add(l[1], x);
}
else if (op=="D")
{
scanf("%d", &k);
erase(k+1);
}
else if (op=="IL")
{
scanf("%d%d", &k, &x);
add(l[k+1], x);
}
else if (op=="IR")
{
scanf("%d%d", &k, &x);
add(k+1, x);
}
}
for (int i=r[0]; i!=1; i=r[i]) printf("%d ", e[i]);
return 0;
}
栈与队列:单调队列、单调栈

模拟栈

模拟队列

单调栈
用于找一个数左边或者右边离它最近的且比它小的数
例如3,4,2,7,5
输出-1,3,-1,2,2

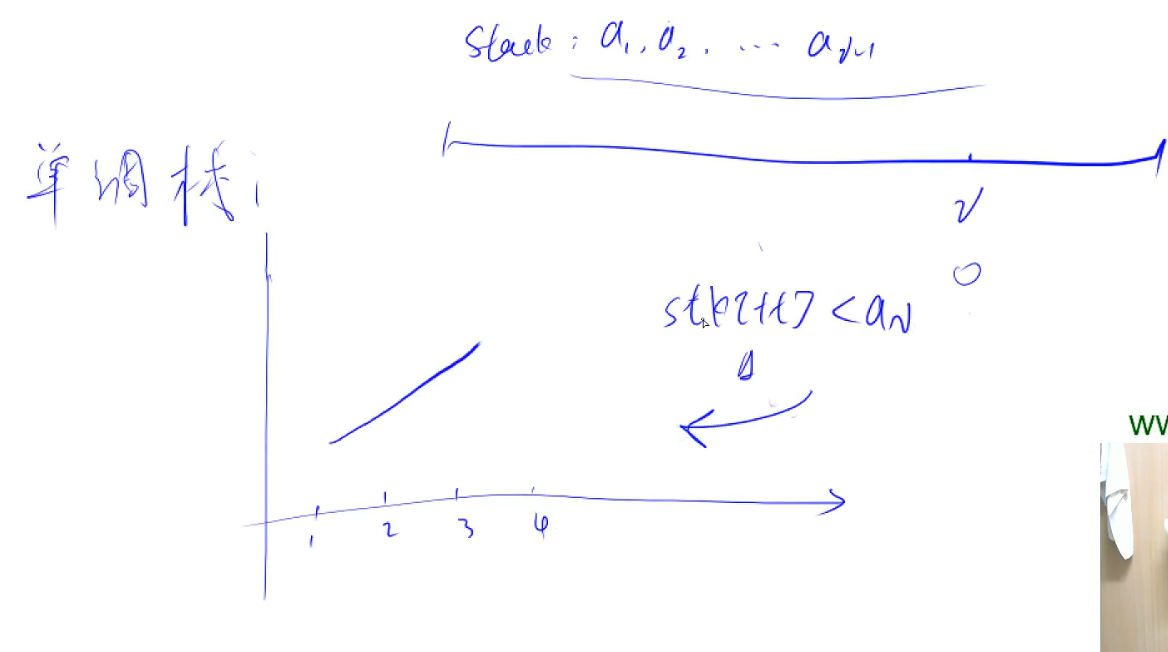
栈里的元素一定是单调上升的
举例,刚开始数组8,7,4,8
8入栈,7再入栈,但是发现,这个8,不仅比7大,而且比7要往左。没用了,就不用管8了
题目信息
题目描述
给定一个长度为 N 的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出 -1。
输入格式
第一行包含整数 N,表示数列长度。
第二行包含 N 个整数,表示整数数列。
输出格式
共一行,包含 N 个整数,其中第i个数表示第i个数的左边第一个比它小的数,如果不存在则输出 -1。
数据范围
1 ≤ N ≤ 1 0 5 10^510
5
1 ≤ 数列中元素 ≤ 1 0 9 10^910
9
输入样例
5
3 4 2 7 5
输出样例
-1 3 -1 2 2
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int n, x, stk[N], tt=0;
int main()
{
scanf("%d", &n);
for (int i=1; i<=n; i++)
{
scanf("%d", &x);
while (tt && stk[tt]>=x) tt--;
if (tt) printf("%d ", stk[tt]);
else printf("-1 ");
stk[++tt]=x;
}
return 0;
}
单调队列
一般用于滑动窗口
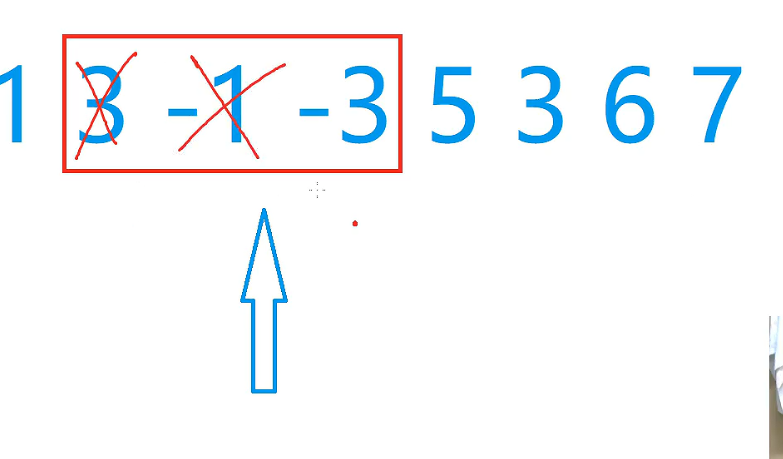
取窗口内最小值, 如果一个数比当前这个数要大,而且位置靠前,就没用了
整个队列在滑动的过程中,在任何时刻都要保证严格的单调递增,因此窗口中的最小值永远是队首。最大值同理
题目来源:AcWing 154. 滑动窗口
一、题目描述
给定一个大小为 n ≤ 1 0 6 n≤10^6n≤10
6
的数组。
有一个大小为 k kk 的滑动窗口,它从数组的最左边移动到最右边。
你只能在窗口中看到 k kk 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子:
该数组为 [1 3 -1 -3 5 3 6 7],k kk 为 3 33。
窗口位置 最小值 最大值
[1 3 -1] -3 5 3 6 7 -1 3
1 [3 -1 -3] 5 3 6 7 -3 3
1 3 [-1 -3 5] 3 6 7 -3 5
1 3 -1 [-3 5 3] 6 7 -3 5
1 3 -1 -3 [5 3 6] 7 3 6
1 3 -1 -3 5 [3 6 7] 3 7
你的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
输入格式
输入包含两行。
第一行包含两个整数 n nn 和 k kk,分别代表数组长度和滑动窗口的长度。
第二行有 n nn 个整数,代表数组的具体数值。
同行数据之间用空格隔开。
输出格式
输出包含两个。
第一行输出,从左至右,每个位置滑动窗口中的最小值。
第二行输出,从左至右,每个位置滑动窗口中的最大值。
输入样例:
8 3
1 3 -1 -3 5 3 6 7
1
2
输出样例:
-1 -3 -3 -3 3 3
3 3 5 5 6 7
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n, k, a[N];
int hh=1, tt=0, q[N];
int main()
{
scanf("%d%d", &n, &k);
for (int i=1; i<=n; i++) scanf("%d", &a[i]);
for (int i=1; i<=n; i++)
{
while (hh<=tt && i-k+1>q[hh]) hh++;
while (hh<=tt && a[q[tt]]>=a[i]) tt--;
q[++tt]=i;
if (i>=k) printf("%d ", a[q[hh]]);
}
printf("\n");
hh=1, tt=0;
for (int i=1; i<=n; i++)
{
while (hh<=tt && i-k+1>q[hh]) hh++;
while (hh<=tt && a[q[tt]]<=a[i]) tt--;
q[++tt]=i;
if (i>=k) printf("%d ", a[q[hh]]);
}
return 0;
}
KMP
sz算法,搞那么复杂,我就直接铥了。
AcWing 831. KMP字符串_acwing的kmp字符串-CSDN博客
KMP算法详解-彻底清楚了(转载+部分原创) - sofu6 - 博客园 (cnblogs.com)
“这玩意像老鼠屎一样,万年难得一用,不用细节就忘,忘了又回来看,过半年又忘”
例题
P3375 【模板】KMP - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
string s, p;
int n=0, m=0, ne[N];
int main()
{
// s[]是长文本,p[]是模式串,n是s的长度,m是p的长度
cin>>s>>p;
s=' '+s, p=' '+p;
n=s.size()-1, m=p.size()-1;
//求模式串的Next数组:
for (int i=2, j=0; i<=m; i++)
{
while (j && p[i]!=p[j+1]) j=ne[j];
if (p[i]==p[j+1]) j++;
ne[i]=j;
}
//匹配
for (int i=1, j=0; i<=n; i++)
{
while (j && s[i]!=p[j+1]) j=ne[j];
if (s[i]==p[j+1]) j++;
if (j==m) //匹配成功
{
printf("%d\n", i-m+1);
j=ne[j];
}
}
for (int i=1; i<=m; i++) printf("%d ", ne[i]);
return 0;
}
Trie
建树例子
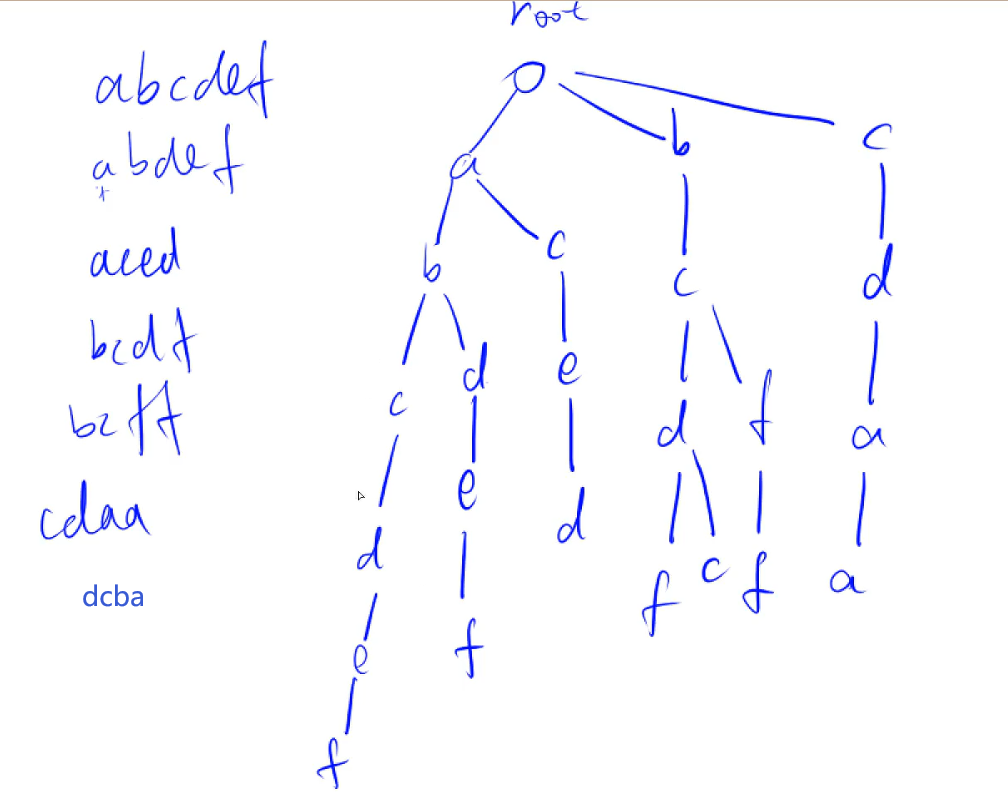
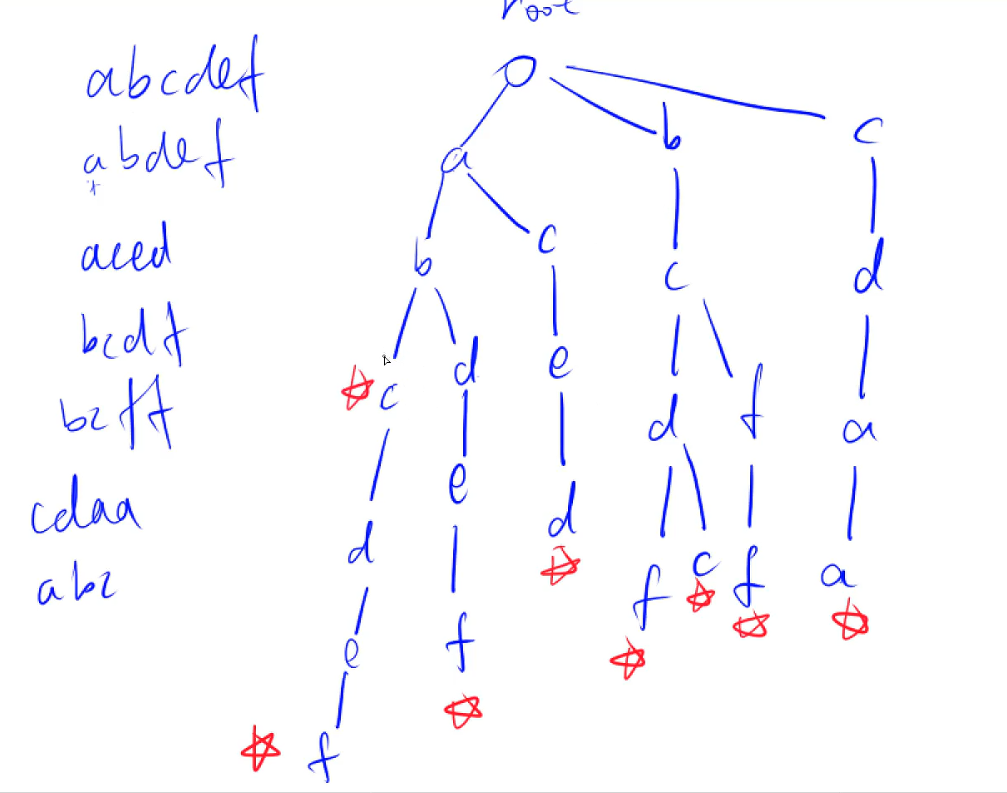
一般存完一个字符串要打上一个标记,在字符串的末尾(也可以是全部单词,如果求前缀的话)
清除字典数组的时候,不能用memset,会超时,要for循环到idx即可
#include <bits/stdc++.h>
using namespace std;
const int N=3e6+5;
int t, n, m, son[N][70], cnt[N], idx=0;
char s[N];
int ctoi(char x)
{
if (x>='A' && x<='Z') return x-'A'+1;
else if (x>='a' && x<='z') return x-'a'+27;
else if (x>='0' && x<='9') return x-'0'+53;
}
void insert(char c[])
{
int p=0;
for (int i=1; c[i]; i++)
{
int u=ctoi(c[i]);
if (!son[p][u]) son[p][u]=++idx;
p=son[p][u];
}
cnt[p]++;
}
int query(char c[])
{
int p=0;
for (int i=1; c[i]; i++)
{
int u=ctoi(c[i]);
if (!son[p][u]) return 0;
p=son[p][u];
}
return cnt[p];
}
int main()
{
scanf("%d", &t);
while (t--)
{
for (int i=0; i<=idx; i++)
for (int j=0; j<=68; j++)
son[i][j]=0, cnt[i]=0;
idx=0;
scanf("%d%d", &n, &m);
for (int i=1; i<=n; i++)
{
scanf("%s", s+1);
insert(s);
}
for (int i=1; i<=m; i++)
{
scanf("%s", s+1);
printf("%d\n", query(s));
}
}
return 0;
}
P8306 【模板】字典树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
并查集

(1)朴素并查集:
int p[N]; //存储每个点的祖宗节点
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
(2)维护size的并查集:
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合:
size[find(b)] += size[find(a)];
p[find(a)] = find(b);
堆
这里维护小根堆

第三点,因为下标为1的数是最小值,但是不好删除,所以删最后一个点,好删一点
第四点,要分情况讨论,是down还是up,因为如果满足一些条件是不会执行down,up的,所以两个都写一遍
down,当一个数变大了,要往下调整
up,当一个数变小了,要往上调整
时间复杂度 O(nlogn)
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n, m, h[N], se=0;
void down(int u) //logn的时间,因为跟层数有关
{
int t=u;
if (u*2<=se && h[u*2]<h[t]) t=u*2;
if (u*2+1<=se && h[u*2+1]<h[t]) t=u*2+1;
if (t!=u)
{
swap(h[u], h[t]);
down(t);
}
}
int main()
{
scanf("%d", &n);
for (int i=1; i<=n; i++) scanf("%d", &h[i]);
se=n;
for (int i=n/2; i>=1; i--) down(i); // 1.*************分析时间***************
while (n--)
{
printf("%d ", h[1]);
h[1]=h[se--];
down(1);
}
return 0;
}
分析一下,1处时间
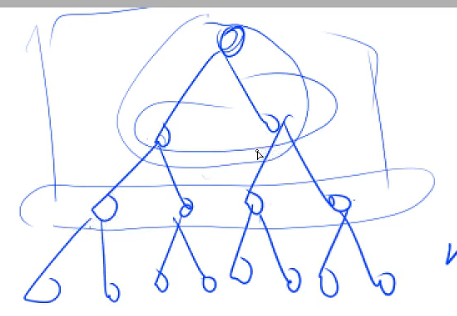
已知最后一层结点数为n/2,倒数第二层为n/4,第三层为n/8,第四层为n/16
因为最后一层不用下降了,所以不用加
然后倒数第二层最多down操作下降1层, 第三层最多down操作下降2层,第四层最多down操作下降3层,累加一下
n/4*1+n/8*2+n/16*3
转换成 n(1/4+2/8+3/16) =》 n(1/22+1/23+1/24)
令S=1/22+1/23+1/24
则2S=1/2+1/22+1/23
2S-S=S=1/2-1/24
已知S<1,所以nS<n,约等于log(n)
为什么建堆要从2分之n开始down?
AcWing 838. 堆排序 分析i=n/2 - AcWing
up操作
void up(int u)
{
while (u/2 && h[u/2]>h[u])
{
swap(h[u/2], h[u]);
u/=2;
}
}
题目来源:AcWing 839. 模拟堆
一、题目描述
维护一个集合,初始时集合为空,支持如下几种操作:
I x,插入一个数 x xx;
PM,输出当前集合中的最小值;
DM,删除当前集合中的最小值(数据保证此时的最小值唯一);
D k,删除第 k kk 个插入的数;
C k x,修改第 k kk 个插入的数,将其变为 x xx;
现在要进行 N NN 次操作,对于所有第 2 22 个操作,输出当前集合的最小值。
输入格式
第一行包含整数 N NN。
接下来 N NN 行,每行包含一个操作指令,操作指令为 I x,PM,DM,D k 或 C k x 中的一种。
输出格式
对于每个输出指令 PM,输出一个结果,表示当前集合中的最小值。
每个结果占一行。
数据范围
1 ≤ N ≤ 1 0 5 1≤N≤10^51≤N≤10
5
− 1 0 9 ≤ x ≤ 1 0 9 −10^9≤x≤10^9−10
9
≤x≤10
9
数据保证合法。
输入样例:
8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM
1
2
3
4
5
6
7
8
9
输出样例:
-10
6
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n, k, x, h[N], hp[N], ph[N], m=0, se=0;
string op;
void heap_swap(int a, int b)
{
swap(h[a], h[b]);
swap(ph[hp[a]], ph[hp[b]]);
swap(hp[a], hp[b]);
}
void down(int u)
{
int t=u;
if (u*2<=se && h[u*2]<h[t]) t=u*2;
if (u*2+1<=se && h[u*2+1]<h[t]) t=u*2+1;
if (t!=u)
{
heap_swap(t, u);
down(t);
}
}
void up(int u)
{
while (u/2 && h[u/2]>h[u])
{
heap_swap(u/2, u);
u/=2;
}
}
int main()
{
scanf("%d", &n);
while (n--)
{
cin>>op;
if (op=="I")
{
scanf("%d", &x);
se++, m++;
h[se]=x;
hp[se]=m, ph[m]=se;
up(se);
}
else if (op=="PM") printf("%d\n", h[1]);
else if (op=="DM")
{
heap_swap(1, se);
se--;
down(1);
}
else if (op=="D")
{
scanf("%d", &k);
k=ph[k];
heap_swap(k, se);
se--;
down(k), up(k);
}
else if (op=="C")
{
scanf("%d%d", &k, &x);
k=ph[k];
h[k]=x;
down(k), up(k);
}
}
return 0;
}
哈希AcWing 840. 模拟散列表(拉链法+开放寻址法) - AcWing
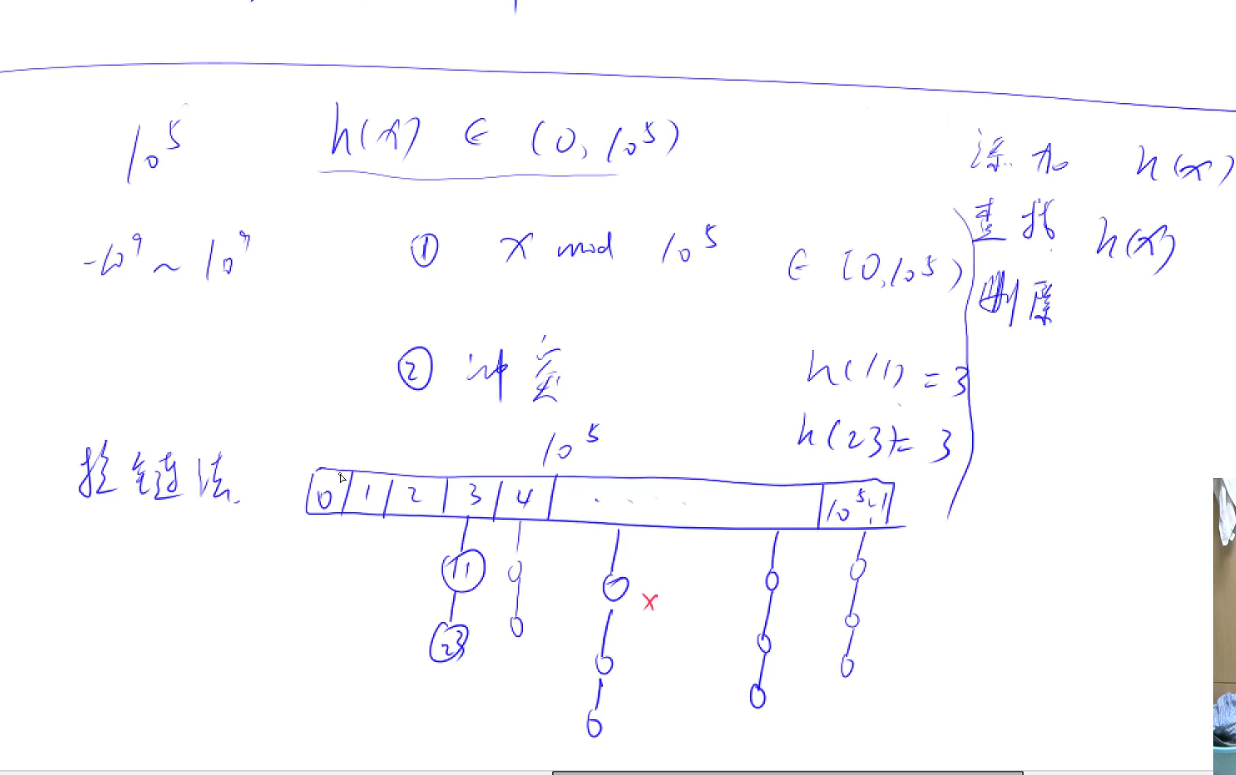
一般先找一个>N的最近质数,作为模数
例如题目范围 1<=N<=1e5
for (int i=1e5;; i++)
{
int flag=1;
for (int j=2; j*j<=i; j++)
if (i%j==0)
{
flag=0;
break;
}
if (flag)
{
cout<<i;
break;
}
}
题目来源:AcWing 840. 模拟散列表
一、题目描述
维护一个集合,支持如下几种操作:
I x,插入一个数 x xx;
Q x,询问数 x xx 是否在集合中出现过;
现在要进行 N NN 次操作,对于每个询问操作输出对应的结果。
输入格式
第一行包含整数 N NN,表示操作数量。
接下来 N NN 行,每行包含一个操作指令,操作指令为 I x,Q x 中的一种。
输出格式
对于每个询问指令 Q x,输出一个询问结果,如果 x xx 在集合中出现过,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1 ≤ N ≤ 1 0 5 1≤N≤10^51≤N≤10
5
− 1 0 9 ≤ x ≤ 1 0 9 −10^9≤x≤10^9−10
9
≤x≤10
9
输入样例:
5
I 1
I 2
I 3
Q 2
Q 5
1
2
3
4
5
6
输出样例:
Yes
No
拉链法:
#include <bits/stdc++.h>
using namespace std;
const int N=100003;
int n, x;
char op;
vector<int> a[N];
void insert(int x)
{
int k=(x%N+N)%N;
a[k].push_back(x);
}
bool find(int x)
{
int k=(x%N+N)%N;
for (int i=0; i<a[k].size(); i++)
if (a[k][i]==x) return true;
return false;
}
int main()
{
scanf("%d", &n);
while (n--)
{
cin>>op;
scanf("%d", &x);
if (op=='I') insert(x);
else if (op=='Q')
{
if (find(x)) printf("Yes\n");
else printf("No\n");
}
}
return 0;
}
开放寻址法
#include <bits/stdc++.h>
using namespace std;
const int N=200003, oo=1e9+5; //比数据范围大一点即可
int n, x, a[N];
char op;
int find(int x)
{
int k=(x%N+N)%N;
while (a[k]!=oo && a[k]!=x)
{
if (k==N) k=0;
k++;
}
return k;
}
int main()
{
for (int i=0; i<N; i++) a[i]=oo;
scanf("%d", &n);
while (n--)
{
cin>>op;
scanf("%d", &x);
int k=find(x);
if (op=='I') a[k]=x;
else if (op=='Q')
{
if (a[k]!=oo) printf("Yes\n");
else printf("No\n");
}
}
return 0;
}
字符串哈希

注意,1.单个字母不能映射成0,
2.人品够好,不存在冲突
一般P取131或13331,Q取2^64


AcWing 841. 字符串哈希 【公式助理解】 - AcWing
[AcWing]841. 字符串哈希(C++实现)-CSDN博客
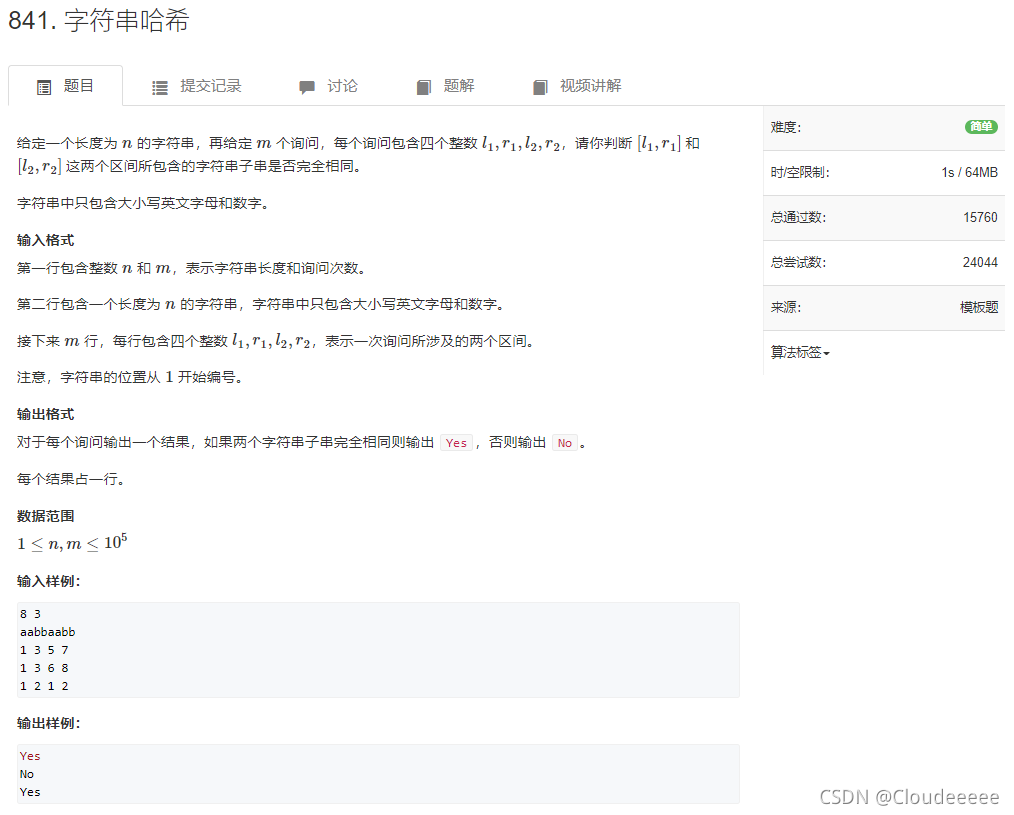
输入:
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
const int N=1e5+5, P=131;
int n, m, l1, r1, l2, r2;
ULL p[N], h[N];
char a[N];
ULL get(int L, int R)
{
return h[R]-h[L-1]*p[R-L+1];
}
int main()
{
scanf("%d%d%s", &n, &m, a+1);
p[0]=1;
for (int i=1; i<=n; i++)
{
p[i]=p[i-1]*P;
h[i]=h[i-1]*P+a[i];
}
while (m--)
{
scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
if (get(l1, r1)==get(l2, r2)) printf("Yes\n");
else printf("No\n");
}
return 0;
}
STL
vector, 变长数组,倍增的思想
size() 返回元素个数
empty() 返回是否为空
clear() 清空
front()/back()
push_back()/pop_back()
begin()/end()
[]
支持比较运算,按字典序
pair<int, int>
first, 第一个元素
second, 第二个元素
支持比较运算,以first为第一关键字,以second为第二关键字(字典序)
string,字符串
size()/length() 返回字符串长度
empty()
clear()
substr(起始下标,(子串长度)) 返回子串
c_str() 返回字符串所在字符数组的起始地址
queue, 队列
size()
empty()
push() 向队尾插入一个元素
front() 返回队头元素
back() 返回队尾元素
pop() 弹出队头元素
priority_queue, 优先队列,默认是大根堆
size()
empty()
push() 插入一个元素
top() 返回堆顶元素
pop() 弹出堆顶元素
定义成小根堆的方式:priority_queue<int, vector<int>, greater<int>> q;
stack, 栈
size()
empty()
push() 向栈顶插入一个元素
top() 返回栈顶元素
pop() 弹出栈顶元素
deque, 双端队列
size()
empty()
clear()
front()/back()
push_back()/pop_back()
push_front()/pop_front()
begin()/end()
[]
set, map, multiset, multimap, 基于平衡二叉树(红黑树),动态维护有序序列
size()
empty()
clear()
begin()/end()
++, -- 返回前驱和后继,时间复杂度 O(logn)
set/multiset
insert() 插入一个数
find() 查找一个数
count() 返回某一个数的个数
erase()
(1) 输入是一个数x,删除所有x O(k + logn)
(2) 输入一个迭代器,删除这个迭代器
lower_bound()/upper_bound()
lower_bound(x) 返回大于等于x的最小的数的迭代器
upper_bound(x) 返回大于x的最小的数的迭代器
map/multimap
insert() 插入的数是一个pair
erase() 输入的参数是pair或者迭代器
find()
[] 注意multimap不支持此操作。 时间复杂度是 O(logn)
lower_bound()/upper_bound()
unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表
和上面类似,增删改查的时间复杂度是 O(1)
不支持 lower_bound()/upper_bound(), 迭代器的++,--
bitset, 圧位
bitset<10000> s;
~, &, |, ^
>>, <<
==, !=
[]
count() 返回有多少个1
any() 判断是否至少有一个1
none() 判断是否全为0
set() 把所有位置成1
set(k, v) 将第k位变成v
reset() 把所有位变成0
flip() 等价于~
flip(k) 把第k位取反
vector中,a有3个元素,为4,4,4,b有4个元素,为3,3,3,3
如果用比较的话,结果是 a>b 的
3中vector的输出方式

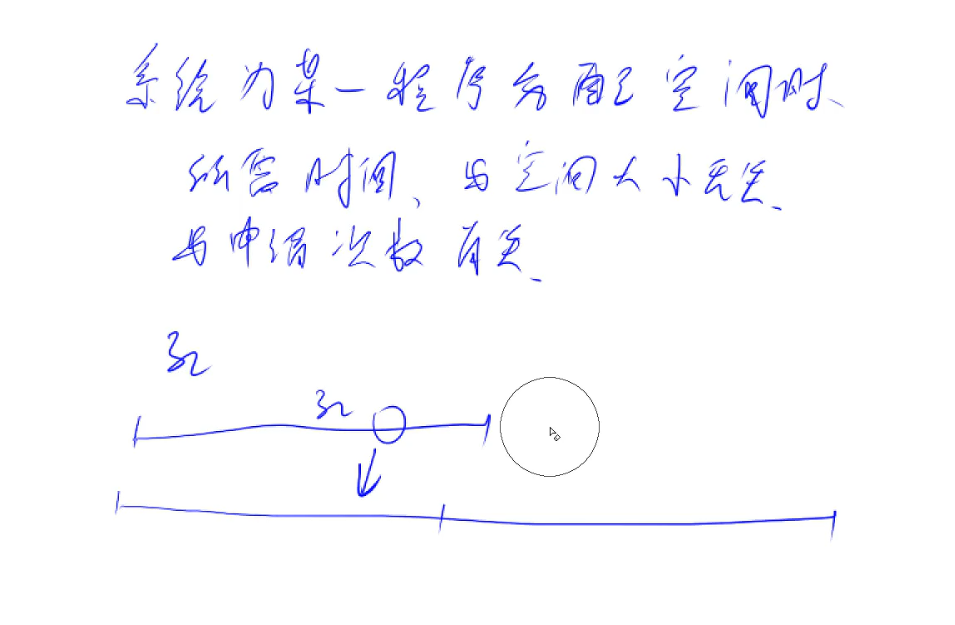
a数组加入1000次元素1,空间长度为1,,与 加入1次,空间长度为1000,元素值为1,后者会更快,因为系统分配空间与内存无关,与申请次数有关
vector的分配空间类似于倍增,例如刚开始开32的空间,发现不够,就开64,一直这样,开n次,就是logn的时间复杂度,每一次相当于O(1)的时间复杂度
pair中,a={1,2}和a=make_pair(1,2)是等价的

如果用pair排序,是可以直接排序的,

pair存储三种东西也可以的
常用:排序,把需要排序的东西放first里面,不需要的放到second里面
字符串用格式化输出为
printf("%s", a.c_str());
priority_queue
一开始默认大根堆,就是堆
想要变成小根堆方法:
1.插入元素改成负数,取出来的时候再变正即可
2.直接定义小根堆

deque速度较慢,注意!

multimap
/*
*
********************************************
* multimap多重映照容器的基础说明:
********************************************
*
* multimap多重映照容器:容器的数据结构采用红黑树进行管理
* multimap的所有元素都是pair:第一元素为键值(key),不能修改;第二元素为实值(value),可被修改
*
* multimap特性以及用法与map完全相同,唯一的差别在于:
* 允许重复键值的元素插入容器(使用了RB-Tree的insert_equal函数)
* 因此:
* 键值key与元素value的映照关系是多对多的关系
* 没有定义[]操作运算
*
* Sorted Associative Container Pair Associative Container Unique Associative Container
*
* 使用multimap必须使用宏语句#include <map>
*
**************************************************************************************
*
* 创建multimap对象:
* 1.multimap<char,int,greater<char> > a; //元素键值类型为char,映照数据类型为int,键值的比较函数对象为greater<char>
* 2.multimap(const key_compare& comp) //指定一个比较函数对象comp来创建map对象
* 3.multimap(const multisetr&); //multimap<int,char*> b(a); //此时使用默认的键值比较函数less<int>
* 4.multimap(first,last);
* 5.multimap(first,last,const key_compare& comp);
*
* //Example:
* pair<const int ,char> p1(1,'a');
* pair<const int ,char> p2(2,'b');
* pair<const int ,char> p3(3,'c');
* pair<const int ,char> p4(4,'d');
* pair<const int ,char> pairArray[]={p1,p2,p3,p4};
* multimap<const int,char> m4(pairArray,pairArray+5);
* multimap<const int,char> m3(m4);
* multimap<const int,char,greater<const int> > m5(pairArray,pairArray+5,greater<const int>());
*
**************************************************************************************
*
* 元素的插入
* //typedef pair<const key,T> value_type;
* pair<iterator,bool> insert(const value_type& v);
* iterator insert(iterator pos,const value_type& v);
* void insert(first,last);
*
**************************************************************************************
*
* 元素的删除
* void erase(iterator pos);
* size_type erase(const key_type& k); //删除等于键值k的元素
* void erase(first,last); //删除[first,last)区间的元素
* void clear();
*
**************************************************************************************
*
* 访问与搜索
*
* iterator begin();iterator end(); //企图通过迭代器改变元素是不被允许的
* reverse_iterator rbegin();reverse_iterator rend();
*
* iterator find(const key_type& k) const;
* pair<iterator,iterator> equal_range(const key_type& k) const;//返回的pair对象,
* //first为lower_bound(k);大于等于k的第一个元素位置
* //second为upper_bound();大于k的第一个元素位置
*
* 其它常用函数
* bool empty() const;
* size_type size() const;
* size_type count(const key_type& k) const; //返回键值等于k的元素个数
* void swap();
*
* iterator lower_bound();iterator upper_bound();pair<iterator,iterator> equal_range();//上界、下届、确定区间
*
*
*
********************************************
** cumirror ** tongjinooo@163.com ** **
********************************************
*
*/
#include <map>
#include <string>
#include <iostream>
// 基本操作与set类型,牢记map中所有元素都是pair
// 对于自定义类,初学者会觉得比较函数如何构造很麻烦,这个可以参照前面的书写示例
// 但若设置键值为int或char类型,无须构造比较函数
struct student{
char* name;
int age;
char* city;
char* phone;
};
int main()
{
using namespace std;
student s[]={
{"童进",23,"武汉","XXX"},
{"老大",23,"武汉","XXX"},
{"饺子",23,"武汉","XXX"},
{"王老虎",23,"武汉","XXX"},
{"周润发",23,"武汉","XXX"},
{"周星星",23,"武汉","XXX"}
};
pair<int,student> p1(4,s[0]);
pair<int,student> p2(2,s[1]);
pair<int,student> p3(3,s[2]);
pair<int,student> p4(4,s[3]); //键值key与p1相同
pair<int,student> p5(5,s[4]);
pair<int,student> p6(6,s[5]);
multimap<int,student> a;
a.insert(p1);
a.insert(p2);
a.insert(p3);
a.insert(p4);
a.insert(p5);
a.insert(p6);
typedef multimap<int,student>::iterator int_multimap;
pair<int_multimap,int_multimap> p = a.equal_range(4);
int_multimap i = a.find(4);
cout<<"班上key值为"<< i->first<<"的学生有:"<<a.count(4)<<"名,"<<" 他们是:"<<endl;
for(int_multimap k = p.first; k != p.second; k++)
{
cout<<k->second.name<<endl;
}
cout<<"删除重复键值的同学"<<endl;
a.erase(i);
cout<<"现在班上总人数为:"<<a.size()<<". 人员如下:"<<endl;
for(multimap<int,student>::iterator j=a.begin(); j != a.end(); j++)
{
cout<<"The name: "<<j->second.name<<" "<<"age: "<<j->second.age<<" "
<<"city: "<<j->second.city<<" "<<"phone: "<<j->second.phone<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号