排队(利用step by step解题)(动态规划+概率)
您刚刚在超市购物,然后前往结账。有两条队伍可用。第一个队伍目前有len1人,而第二个队伍有len2人。你想知道排在第一个队伍比排在第二条队伍“好”(即更早轮到你)的概率。第一个队伍的收银员准备开始给第一个队伍的第一个人结账。第二个队伍的收银员准备开始给第二个队伍的第一个人结账。结账的时间取决于收银员的经验。
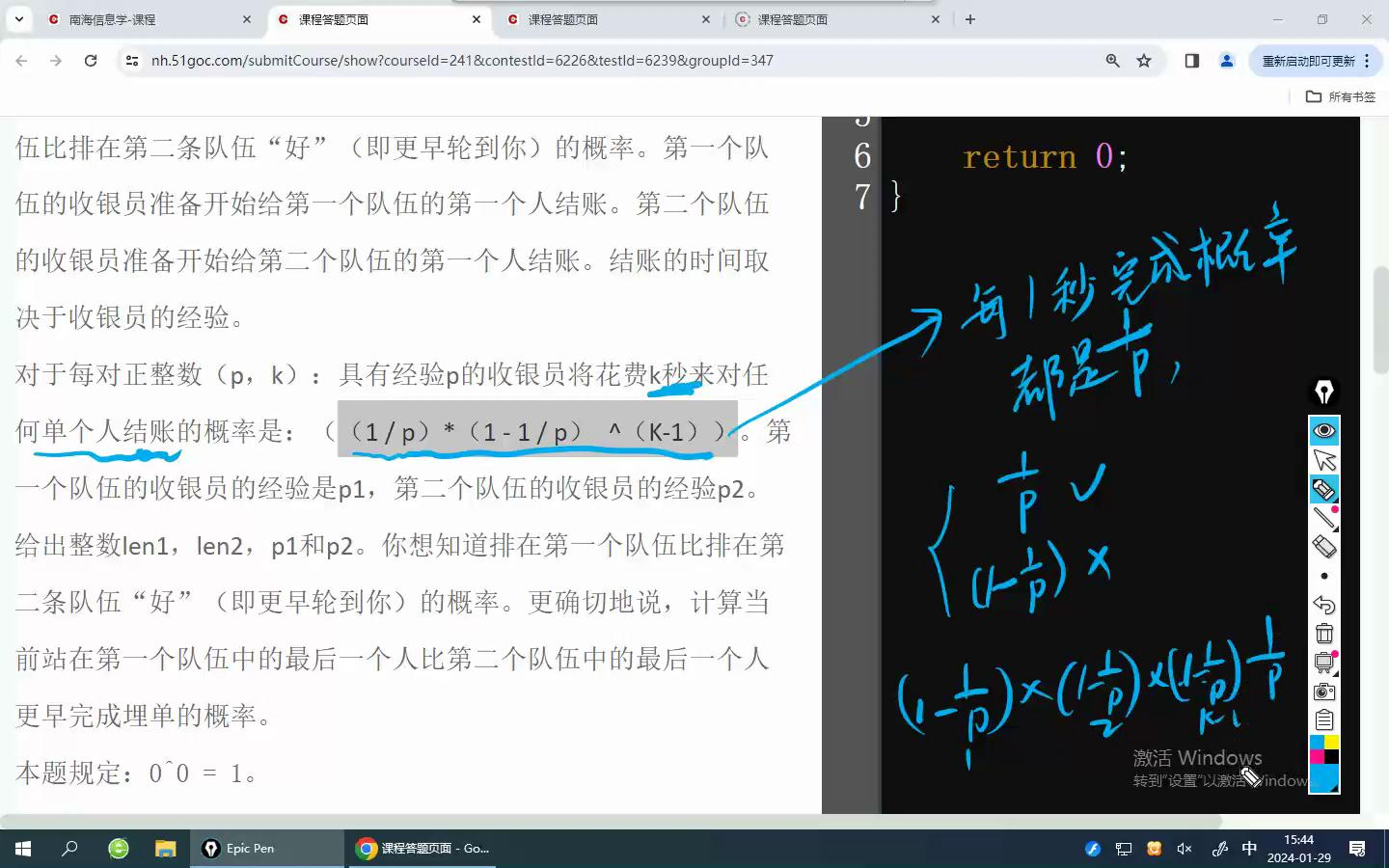
对于每对正整数(p,k):具有经验p的收银员将花费k秒来对任何单个人结账的概率是:((1 / p)*(1 - 1 / p) ^(K-1))。第一个队伍的收银员的经验是p1,第二个队伍的收银员的经验p2。给出整数len1,len2,p1和p2。你想知道排在第一个队伍比排在第二条队伍“好”(即更早轮到你)的概率。更确切地说,计算当前站在第一个队伍中的最后一个人比第二个队伍中的最后一个人更早完成埋单的概率。
本题规定:0^0 = 1。
输入格式
多组测试数组。
第一行,一个整数G。表示有G组测试数据。1 <= G <= 10。
每组测试数据格式如下:
一行,len1,len2,p1,p2。 1 <= len1,len2,p1,p2 <= 1000。
输出格式
共G行,每行一个实数。误差不能超过0.000000001。
输入/输出例子1
输入:
10
1 2 2 1
1 3 3 7
3 1 7 3
12 34 56 78
3 6 8 4
739 472 691 138
604 259 303 513
167 303 405 276
677 533 589 380
289 491 826 606
输出:
0.5
0.9835390946502058
0.010973936899862834
0.999996203228025
0.5229465300297028
0.0
5.156019002856837E-6
0.9872711986032693
0.0
0.9986698635516139
样例解释
无
1.DP数组题目所求有一定联系(比如状态表示题目要求的答案,维度跟第几个,什么价值有一定关系)
2.循环从小到大还是从大到小取决于后一项跟前一项的关系,后一项跟前一项有关就是从小到大
以上总结可能不一定,先对dp有了一定初步的了解
发现这题的队伍长度,还是有一些关联的,考虑动态规划求解
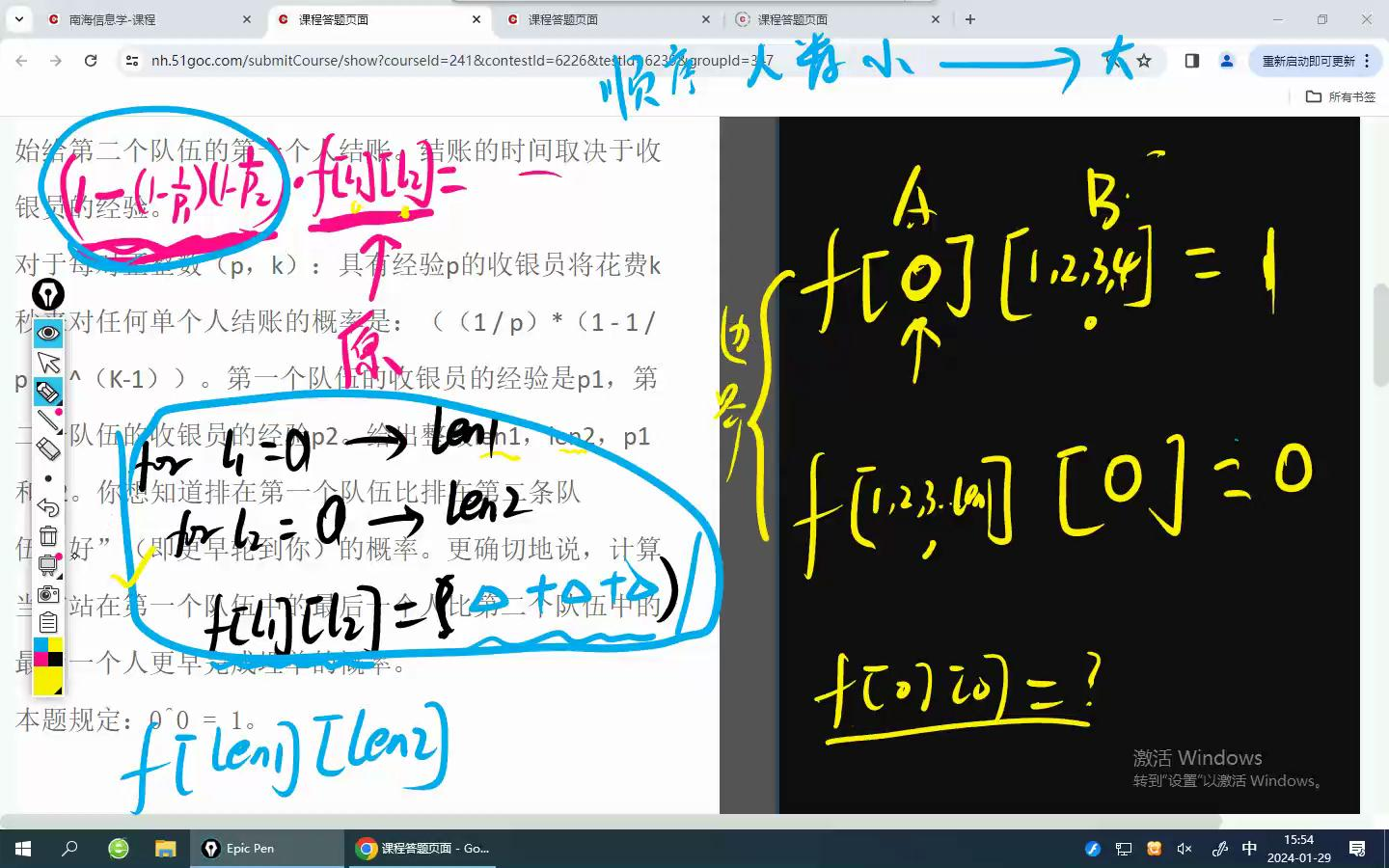
f[len1][len2]表示A有len1,人,B有len2人,A比B好的概率
那么下一秒结账,A可能结账成功,B可能失败,记为X1;A可能成功,B可能成功,记为X2;A可能失败,B可能成功,记为X3;A可能失败,B可能失败,记为X4
分4种情况,根据“每一秒完成的概率都是1/p”,容易推出
X1=(1.0/p1)*(1.0-(1.0/p2))*f[i-1][j] 1/p1的概率,A成功;1-1/p2的概率,B成功;两概率相乘,A结账成功,队伍人数减少1人;B结账失败,队伍人数不边
X2=(1.0/p1)*(1.0/p2)*f[i-1][j-1]; 1/p1的概率,A成功;1/p2的概率,B成功;两概率相乘,A结账成功,队伍人数减少1人;B结账成功,队伍人数减少1人
X3=(1.0-(1.0/p1))*(1.0/p2)*f[i][j-1] 1-1/p1的概率,A失败;1/p2的概率,B成功;两概率相乘,A结账失败,队伍人数不边;B结账成功,队伍人数减少1人
X4=(1.0-(1.0/p1))*(1.0-(1.0/p2))*f[i][j] 1-1/p1的概率,A失败;1-1/p2的概率,B失败;两概率相乘,A结账失败,队伍人数不边;B结账失败,队伍人数不边
边=>变,懒得改了,能看懂
然后四种情况相加,得
f[i][j]=X1+X2+X3+X4
可是X4包含f[i][j],不好求,移项
1-( (1.0-(1.0/p1))*(1.0-(1.0/p2)) ) *f[i][j]=X1+X2+X3
于是推出了状态转移方程
外内循环都是从小到大,因为要先知道小的,才能知道大的,后一项跟前一项有关

考虑一下答案,那肯定就是f[len1][len2]了
边界就是考虑len1=0,或者len2=0了
A走完,B不管有多少人,A都100%好
A不管有多少人,B走完,A都100%不好
A走完,B也走完,那无法确定A先走还是B先走,定为A,100%不好
#include <bits/stdc++.h>
using namespace std;
const int N=1005;
int g, c1, c2, p1, p2;
double f[N][N];
int main()
{
scanf("%d", &g);
while (g--)
{
memset(f, 0, sizeof f);
scanf("%d%d%d%d", &c1, &c2, &p1, &p2);
//边界
for (int i=1; i<=c1; i++) f[i][0]=0;
for (int i=1; i<=c2; i++) f[0][i]=1;
f[0][0]=0;
for (int i=1; i<=c1; i++) //队伍长度至少1,题目范围有说
for (int j=1; j<=c2; j++)
{
//转移方程
double a=(1.0/p1)*(1.0/p2)*f[i-1][j-1];
double b=(1.0/p1)*(1.0-(1.0/p2))*f[i-1][j];
double c=(1.0-(1.0/p1))*(1.0/p2)*f[i][j-1];
double d=(1.0-(1.0/p1))*(1.0-(1.0/p2)); //注意没有*f[i][j]了
f[i][j]=(a+b+c)*1.0/(1.0-d); //转成除法
}
printf("%.16lf\n", f[c1][c2]);
}
return 0;
}
/*
注释是错误,没改过来,别认真看。。。
1 1
1.0/p1*1.0/p2*f[i-1][j-1]
1 0
1.0/p1*(1.0-(1.0/p2))*f[i-1][j]
0 1
(1.0-(1.0/p1))*1.0/p2)*f[i][j-1]
0 0
(1.0-(1.0/p1))*(1.0-(1.0/p2))*f[i][j]
*/
ljx:
#include<bits/stdc++.h>
using namespace std;
int g;
double f[1005][1005],ans=0;//f[i][j]表示:l1有i个人 l2有j个人 ,A比B好的概率
int main(){
scanf("%d",&g);
while(g--){
int len1,len2,p1,p2;
ans=0.0;
scanf("%d%d%d%d",&len1,&len2,&p1,&p2);
for(int i=1;i<=len2;i++) f[0][i]=1;
for(int i=1;i<=len1;i++) f[i][0]=0;
f[0][0]=0;
for(int l1=1;l1<=len1;l1++){
for(int l2=1;l2<=len2;l2++){
double a=(1.0/p1*1.0)*(1.0-(1.0/p2*1.0))*f[l1-1][l2];//A 成功 B 不成功
double b=(1.0-(1.0/p1*1.0))*(1.0/p2*1.0)*f[l1][l2-1];//A 不成功 B 成功
double c=(1.0/p1*1.0)*(1.0/p2*1.0)*f[l1-1][l2-1];//A 成功 B 成功
double pro=(1.0-(1.0-(1.0/p1*1.0))*(1.0-(1.0/p2*1.0)));
f[l1][l2]=(a+b+c)*1.0/pro*1.0;
}
}
ans=f[len1][len2]*1.0;
printf("%.16lf\n",ans);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号