掷骰子(概率+动态规划)
玩家A和B正在玩骰子游戏。
A骰子有6个面,第i个面的点数是sideA[i]。
B骰子有6个面,第i个面的点数是sideB[i]。
玩家A总共掷X次A骰子,每次掷骰子得到的面都是1/6的概率。
玩家B总共掷Y次B骰子,每次掷骰子得到的面都是1/6的概率。
玩家最终的总得分就是每次掷骰子得到的点数的总和。
计算玩家A赢得游戏的概率,即玩家A总得分高于玩家B的总得分的概率。
输入格式
组测试数据。
第一行,一个整数G,表示有G组测试数据。 1 <= G <= 10
每组测试数据格式:
第一行,两个整数,X 和 Y。1 <= X,Y <= 200。
第二行,6个整数,第i个整数是sideA[i]。 1 <= sideA[i] <= 100。
第三行,6个整数,第i个整数是sideB[i]。 1 <= sideB[i] <= 100。
输出格式
共G行,共G行,每行一个实数,误差不超过0.0001。
输入/输出例子1
输入:
10
1 1
1 2 3 4 5 6
1 2 3 4 5 6
200 200
1 3 8 18 45 100
1 4 10 21 53 100
2 3
1 1 1 2 2 2
1 1 1 1 1 1
200 200
6 5 4 3 2 1
3 4 6 5 1 2
100 199
1 1 1 1 1 2
1 1 1 1 1 1
1 1
1 2 1 2 1 2
2 1 2 1 2 1
200 80
1 3 8 18 45 100
1 4 10 21 53 100
100 100
1 3 5 10 15 20
9 9 9 9 9 9
100 100
7 8 9 9 10 11
1 3 5 10 15 20
10 1
1 2 3 4 5 6
59 70 80 90 95 100
输出:
0.41666666666666663
0.25240407058279035
0.25
0.49416239842107595
1.5306467074865068E-78
0.25
0.9999999976160046
0.4943375131579816
0.49968090996086173
2.7563619479867007E-9
样例解释
无
可以考虑动态规划解决此问题,因为可以分为每个阶段求解,而且是相关联的,可以推一下
先考虑状态,这题至少要有2个重要条件,一个是掷的骰子数,一个是得到的分数。于是我们用 f[i][j]表示A掷了i次,得到j分,g[i][j]表示B掷了i次,得到j分
状态搞好了,我们考虑一下怎么算答案呢,很简单。假设A,B分别掷10,20次骰子,A得900分,赢得比赛,那么B只能是899~1分(每个骰子最少标有1分,所以是1分),那么我们得到结果(概率相乘)
f[10][900]*(g[20][899]+g[20][898]+g[20][897]+....+g[20][1]
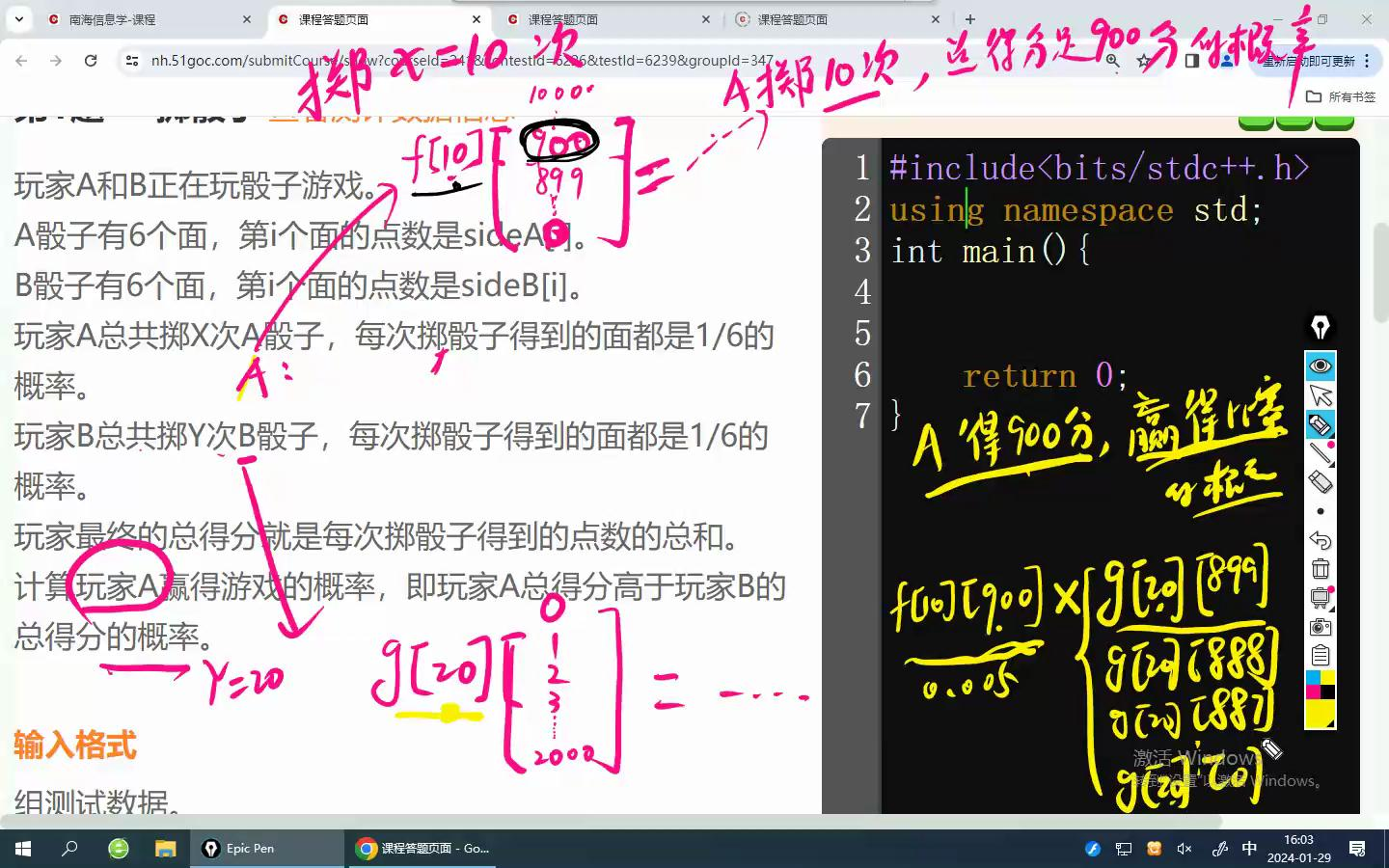
但是这样算出来有点慢,于是前缀和处理g数组结果
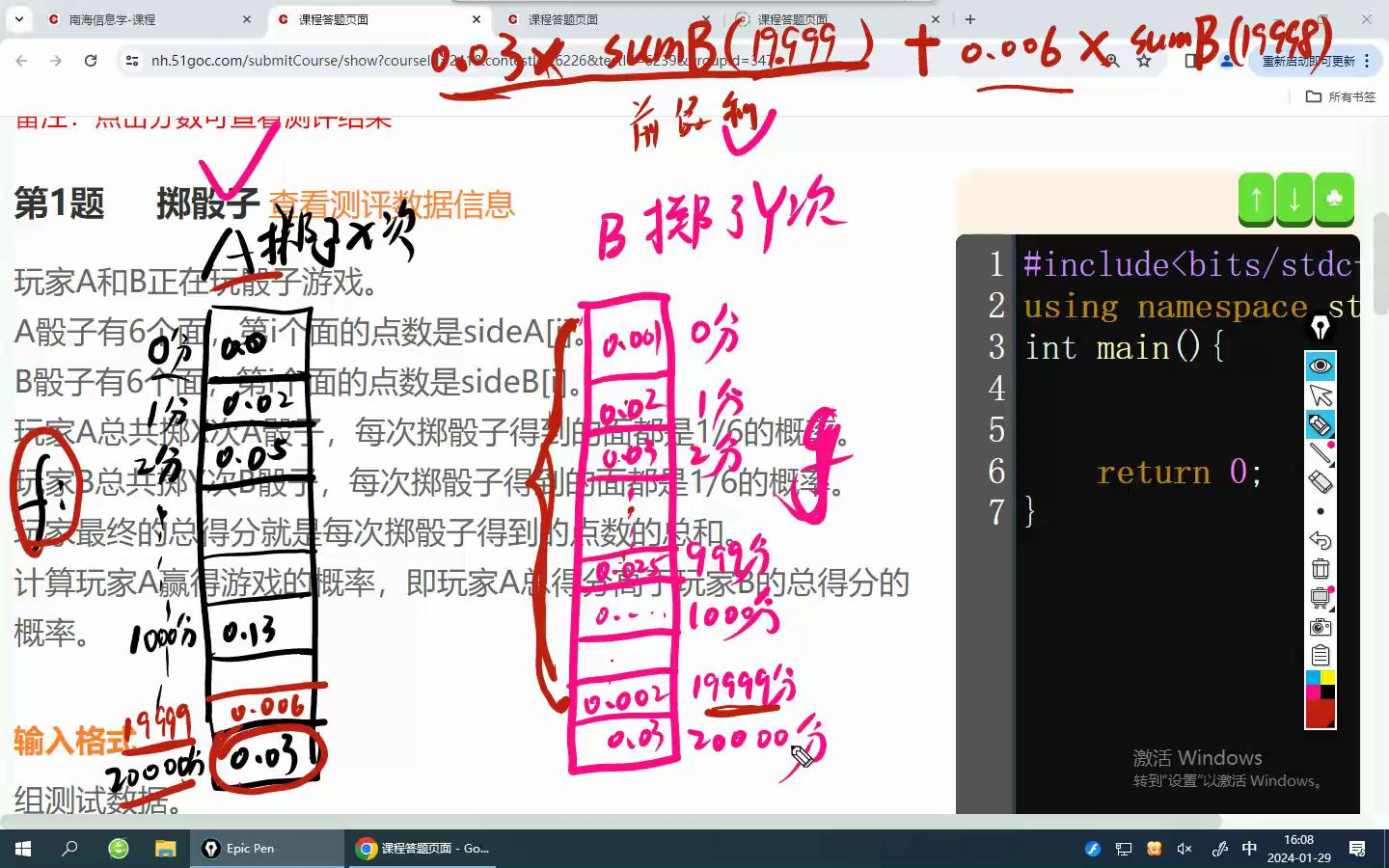
假设A的20000分,概率0.03。那么总结果(只要A比B分数高即可,但是分数不知道,所以从最大分开始找)是
f[x][20000]*(g[y][19999]+....+g[y][1]) +
f[x][19999]*(g[y][19998]+....+g[y][1]) +
..... +
f[x][2]*g[y][1]
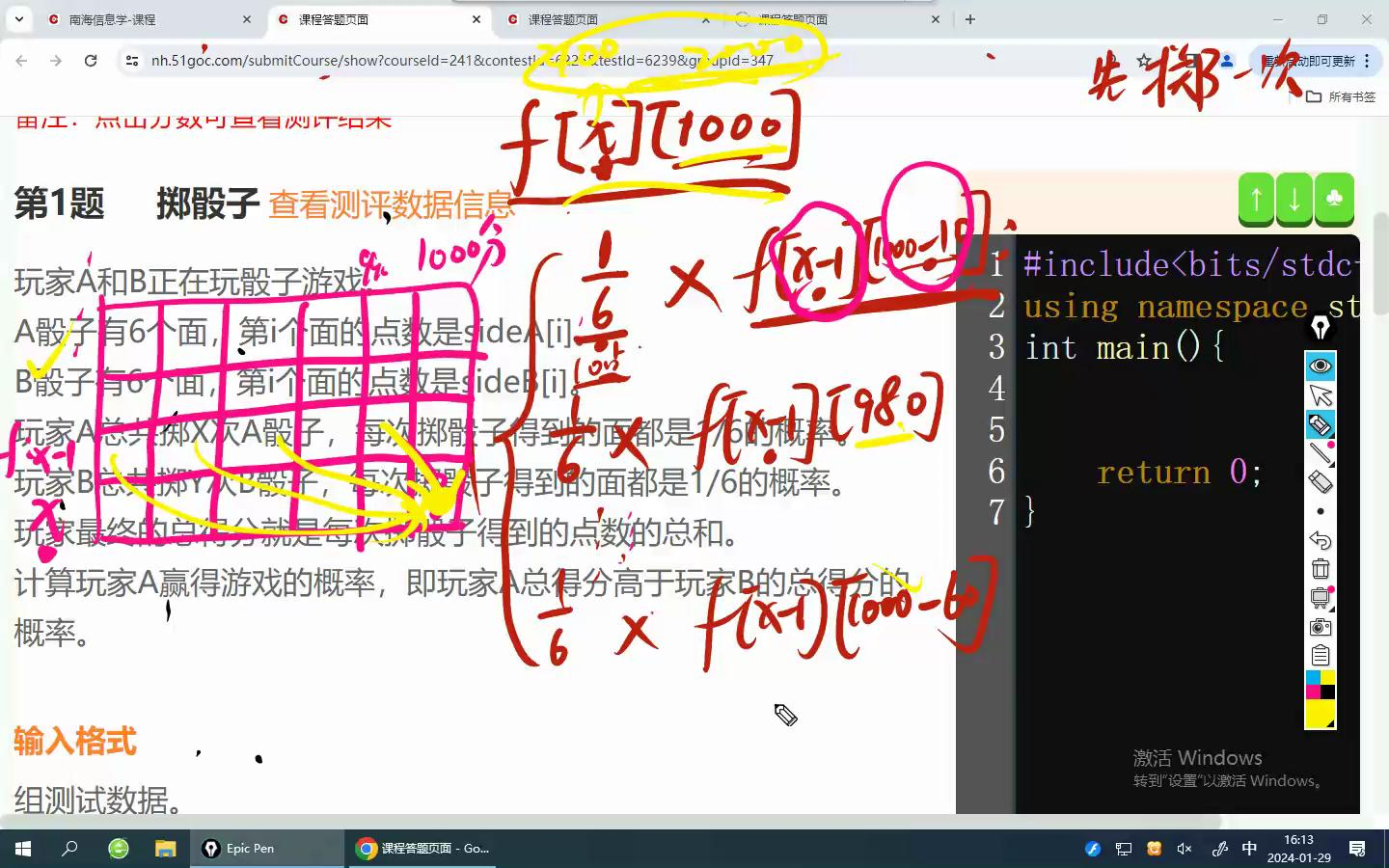
考虑转移方程,假设A掷了x次,得1000分
f[x][1000]=1/6*f[x-1][1000-sizeA[1]]+ 1/6*f[x-1][1000-sizeA[2]] + 1/6*f[x-1][1000-sizeA[3]] .....+ 1/6*f[x-1][1000-sizeA[6]]
那么掷的次数肯定是外循环,跟这个次数有关系,且是从小到大(先知道小的才能知道大的)
然后内循环也是从小到大(1....20000)(先知道小的才能知道大的)
#include <bits/stdc++.h>
using namespace std;
const int N=205, M=20005;
int t, x, y, a[10], b[10];
double f[N][M], g[N][M], ans=0;
int main()
{
scanf("%d", &t);
while (t--)
{
ans=0;
memset(f, 0, sizeof f);
memset(g, 0, sizeof g);
scanf("%d%d", &x, &y);
for (int i=1; i<=6; i++)
scanf("%d", &a[i]);
for (int i=1; i<=6; i++)
scanf("%d", &b[i]);
f[0][0]=g[0][0]=1; //边界定为1,原因是掷0次得到0的概率是100%的,且跟之后的循环有关系,想要f[1][a[i]]=1/cnta(防止重复,cnta是不重复的骰子标的数),这里必须是赋值1
for (int i=1; i<=x; i++)
for (int j=1; j<=20000; j++)
for (int k=1; k<=6; k++)
if (j>=a[k]) f[i][j]+=1/6.0*f[i-1][j-a[k]]; //转移方程
for (int i=1; i<=y; i++)
for (int j=1; j<=20000; j++)
for (int k=1; k<=6; k++)
if (j>=b[k]) g[i][j]+=1/6.0*g[i-1][j-b[k]];
for (int i=1; i<=20000; i++) //前缀和处理
g[y][i]+=g[y][i-1];
for (int i=1; i<=20000; i++)
ans+=f[x][i]*g[y][i-1]; //记答案,知道掷的总次数,但是要枚举分数(因为不知道,都有可能)
printf("%.16lf\n", ans);
}
return 0;
}
ljx: (https://www.luogu.com.cn/blog/ljxsdsg886/zhi-tou-zi)
看完题目后,如果没有思路,那就直接DP吧
总结了初步的dp之后,发现dp的下标都跟题目的未知量有关,比如这题的题目未知量是得分和次数,而本题有两个次数,所以有两个dp数组。想一想这题的状态转移方程,那么f[i][j]表示掷骰子i次可以的到j得分的概率,那么是不是我上一次可以掷到j-sideA[i],然后这一次掷sideA[i]就可以得到这个j分了,那么想要在这一次得到sideA[i],有1/6的概率的得到sideA[i],所以我们就得到转移方程式:
f[i][j]+=f[i-1][j-a[k]]*(1.0/6.0);其实关键的代码只有这一行,不过......
DP初始化还是很重要的
我们这一题的DP数组初始化,首先想到当我掷0次是得到0分的概率,这还用说嘛,不就是1吗,所以初始化应为f[0][0]=1。
好了,我知道你们“像小猫一样粘着”我的代码,那就来吧!!!
#include<bits/stdc++.h>
using namespace std;
int g,a[10],b[10],maxa=INT_MIN,maxb=INT_MIN;
double f[200][20000],f2[200][20000],sumb[200][20000],ans=0.0;
//注意要准备两个DP数组:f和f2,因为分别为X 和 Y的dp数组
int main(){
scanf("%d",&g);
while(g--){
int x,y;
maxa=maxb=INT_MIN;
memset(f,0,sizeof f);
memset(f2,0,sizeof f2);
scanf("%d%d",&x,&y);
for(int i=1;i<=6;i++){
scanf("%d",&a[i]);
maxa=max(maxa,a[i]);
}
for(int i=1;i<=6;i++){
scanf("%d",&b[i]);
maxb=max(maxb,b[i]);
}
maxa*=x;
maxb*=y;
ans=0.0;
f[0][0]=f2[0][0]=1.00;
for(int i=1;i<=x;i++){
for(int j=1;j<=maxa;j++){
for(int k=1;k<=6;k++){
f[i][j]+=f[i-1][j-a[k]]*(1.0/6.0);
}
}
}
for(int i=1;i<=y;i++){
for(int j=1;j<=maxb;j++){
for(int k=1;k<=6;k++){
f2[i][j]+=f2[i-1][j-b[k]]*(1.0/6.0);
}
}
}
for(int i=1;i<=maxa;i++){
for(int j=1;j<i;j++){//因为j的分数一定要比i的分数小(不明白的自己看题目要求什么)
ans+=f[x][i]*f2[y][j];
}
}
printf("%.16lf\n",ans);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号