通信（二分+SPFA好题）

第1题     通信 查看测评数据信息

某城市有 N 座通信基站，P 条 双向 电缆，第 i 条电缆连接基站 Ai 和 Bi。特别地，1 号基站是通信公司的总站，N 号基站位于一座农场中。现在，农场主希望对通信线路进行升级，其中升级第 i 条电缆需要花费 Li。电话公司正在举行优惠活动。农场主可以指定一条从 1 号基站到 N 号基站的路径，并指定路径上不超过 K 条电缆，由电话公司免费提供升级服务。农场主只需要支付在该路径上剩余的电缆中，升级价格最贵的那条电缆的花费即可。

求至少用多少钱可以完成升级。0≤K<N≤1000,1≤P≤10000 ,1≤Li≤1000000


输入格式

第 1 行：三个整数 N，P，K。

第 2..P+1 行：第 i+1 行包含三个整数 Ai,Bi,Li。

输出格式

包含一个整数表示最少花费。

若 1 号基站与 N 号基站之间不存在路径，则输出 −1

输入/输出例子1

输入：

5 7 1

1 2 5

3 1 4

2 4 8

3 2 3

5 2 9

3 4 7

4 5 6


输出：

4

样例解释

无

 

 

分析一下，化简题意就是，1走到n，砍掉一些边，求出剩余边的最大值，使这个最大值最小

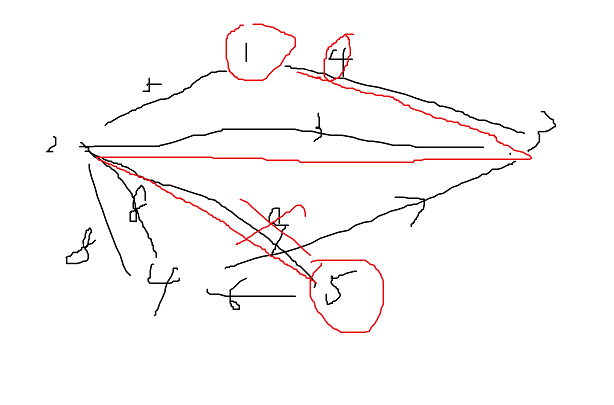
 1走到5，进过1-3（4），3-2（3），2-5（9）
砍掉9，答案是4（4,3的最大值）

那么应该怎么写呢？

我们可以用二分查找，二分砍掉的边的权值。注意，二分不仅仅可以找已知的量，即使不知道这个量也可以二分

例如我们设k=1，二分砍掉的值是5，那么路上遇到>5的值，就设置这条边的权值为1，否则权值为0

 

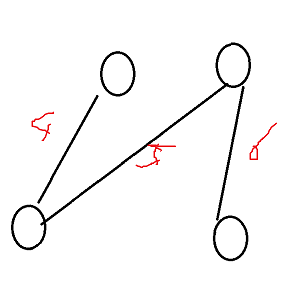
4<=5，权为0；5<=5，权为0；6>5，权为1

那么此图最短路是1，（0+0+1），1<=k，答案有效，所以我们选择砍掉6的边。（如果二分到的值为7，此时应该缩小答案）

但是如果二分砍掉的值是4

4<=4，权为0；5>4，权为1；6>4，权为1

那么最短路会是2（0+1+1），2>k，答案无效。那么此时应该增大答案

非常的巧妙，于是代码出来了

#include <bits/stdc++.h>
using namespace std;

const int N=1e3+5;
struct node
{
	int v, w;
};
int n, p, k, u1, v1, w1, Max=0, dis[N], vis[N], L=0, R=0, ans=-1;
vector<node> a[N];
queue<int> q;
void spfa(int s)
{
	memset(dis, 63, sizeof dis);
	memset(vis, 0, sizeof vis);
	dis[1]=0, q.push(1);
	
	while (!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		
		for (int i=0; i<a[u].size(); i++)
		{
			int v=a[u][i].v, w=a[u][i].w;
			if (dis[v]>dis[u]+(w>s)) //w是边权 s是二分的值 w>s 则设置权为1（需要砍掉），否则为0
			{
				dis[v]=dis[u]+(w>s);
				if (!vis[v]) vis[v]=1, q.push(v);
			}
				
		}
	}
}
bool check(int val)
{
//	cout<<val<<endl;
	spfa(val);
	if (dis[n]>k) return false; //砍的边数>k，无效
	return true; //<=k有效
}
int main()
{
	scanf("%d%d%d", &n, &p, &k);
	for (int i=1; i<=p; i++)
	{
		scanf("%d%d%d", &u1, &v1, &w1);
		a[u1].push_back({v1, w1});
		a[v1].push_back({u1, w1});
		Max=(Max, w1); //记录最大边权
	}
	L=0, R=Max; //有可能全砍，所以L=0，有可能全不砍，所以R=最大边权
	while (L<=R)
	{
		int mid=(L+R)/2;
		if (check(mid)) ans=mid, R=mid-1; //发现答案有效，即可缩小右端点，找一个更小值
		else L=mid+1; //否则继续扩大，找一个更大的值
	}
	
	printf("%d", ans); //默认-1
	return 0;
}