有边数限制的最短路（动态规划）

第3题     有边数限制的最短路 查看测评数据信息

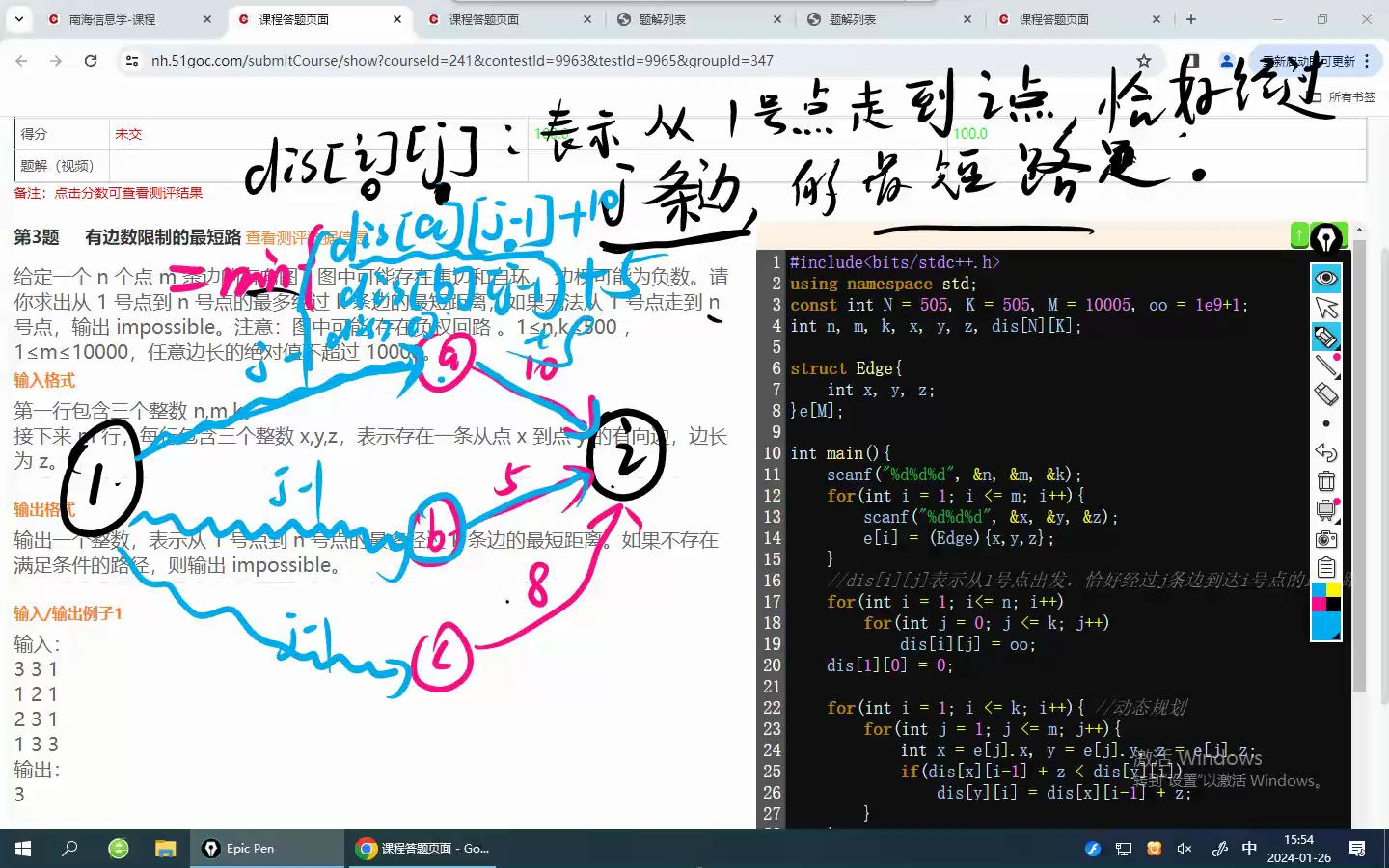
给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出 impossible。注意：图中可能 存在负权回路 。1≤n,k≤500 ，1≤m≤10000，任意边长的绝对值不超过 10000。

输入格式

 

第一行包含三个整数 n,m,k。

接下来 m 行，每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

 

输出格式

 

输出一个整数，表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。如果不存在满足条件的路径，则输出 impossible。

 

输入/输出例子1

输入：

3 3 1

1 2 1

2 3 1

1 3 3

 

输出：

3

 

样例解释

无

 

 

 

这题其实并不算Bellman-ford的题，应该是动态规划

 

 

 

 

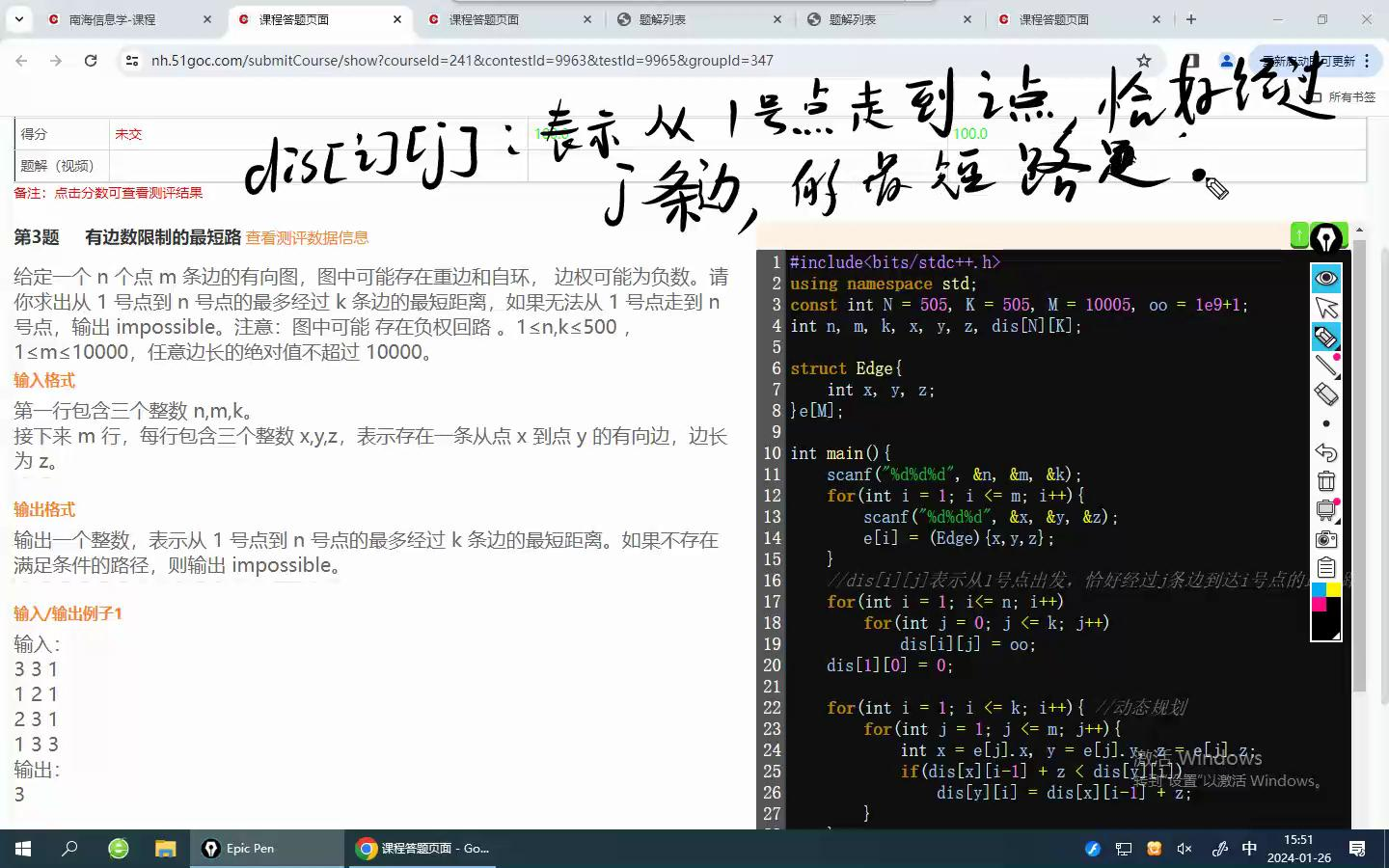
#include <bits/stdc++.h>
using namespace std;

const int N=1e4+5, M=505;
struct edge
{
	int u, v, w;
}a[N];
int n, m, k, x, y, z;
int dis[N][M], ans=0;
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for (int i=1; i<=m; i++)
    {
    	scanf("%d%d%d", &x, &y, &z);
    	a[i]={x, y, z};
	}
	
	memset(dis, 63, sizeof dis);
    ans=dis[0][0];
	dis[1][0]=0;
	
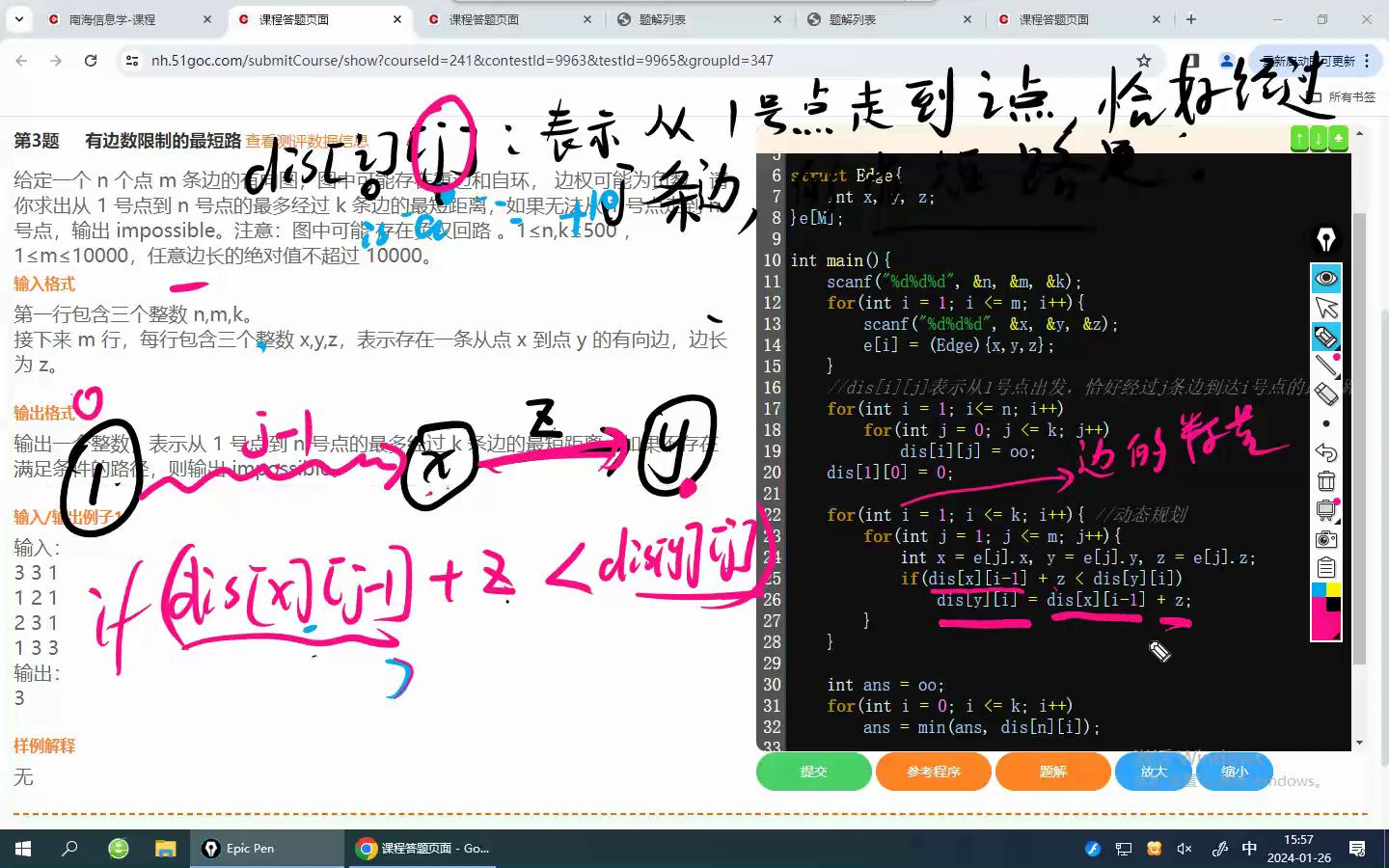
	for (int i=1; i<=k; i++) //松弛k轮并不可行，并不一定松弛了k条边，所以这里的i表示边数
	{
		for (int j=1; j<=m; j++)
		{
			int u=a[j].u, v=a[j].v, w=a[j].w;
			if (dis[u][i-1]+w<dis[v][i]) //u点是起点，到起点需要减1条边，然后加上u点到v点的距离，这样就是dis[v][i]了
				dis[v][i]=dis[u][i-1]+w;
		} 
	}
	
	for (int i=0; i<=k; i++) ans=min(ans, dis[n][i]); 
	
    
    if (ans<dis[0][0]) printf("%d", ans);
    else printf("impossible");
    return 0;
}