拓扑排序-奖金 （拓扑排序）

第3题     奖金 查看测评数据信息

由于无敌的凡凡在2005年世界英俊帅气男总决选中胜出，Yali Company总经理Mr.Z心情好，决定给每位员工发奖金。公司决定以每个人本年在公司的贡献为标准来计算他们得到奖金的多少。于是Mr.Z下令召开 m 方会谈。每位参加会谈的代表提出了自己的意见：“我认为员工 a 的奖金应该比 b 高！”Mr.Z决定要找出一种奖金方案，满足各位代表的意见，且同时使得总奖金数最少。每位员工奖金最少为100元，且必须是整数。1≤n≤10000 ,1≤m≤20000

输入格式

 

第一行包含整数 n,m，分别表示公司内员工数以及参会代表数。

接下来 m 行，每行 2 个整数 a,b，表示某个代表认为第 a 号员工奖金应该比第 b 号员工高。

 

输出格式

 

若无法找到合理方案，则输出“Poor Xed”；

否则输出一个数表示最少总奖金。

 

输入/输出例子1

输入：

2 1

1 2

 

输出：

201

 

样例解释

无

 

从“第 a 号员工奖金应该比第 b 号员工高”可知，是拓扑排序

那么排完的序列，我们应该如何算价钱呢？

我们定mo[i]为第i位员工需要的奖金

首先，“每位员工奖金最少为100元”,所以mo[1~n

]都应该初始化为100

那么你会发现（这里定增加金额不固定为1，随意数值）

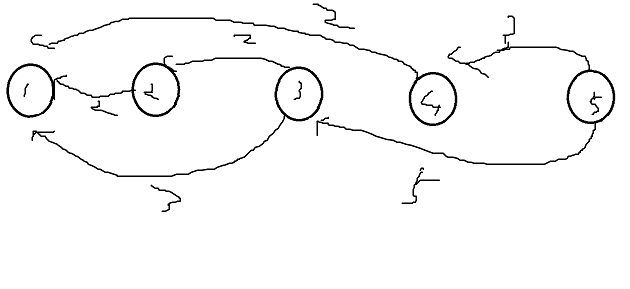
 所有连边都是从右到左的，没有从左到右的，那么我们发现，mo[3]=max(mo[5]+5, mo[3])，于是整题就推出来了

为什么是max？因为！第3位员工，至少比第5位员工要多5块，但是第三位员工的初始奖金是100，你不可能选一个min，取到100的奖金，而是105（员工5没有连边，默认位100即可，所以是100+5）

我们从特殊推广到一般，得出

mo[v]=max(mo[u]+w, mo[v])

u是起点，v是要到的点，w是起点到要到的点的权 （这里的w为1，因为要最小，那就多1块就好了）

最后答案累加每个员工的奖金即可

#include <bits/stdc++.h>
using namespace std;
 
const int N=1e5+5;
vector<int> a[N];
int n, m, u1, v1, d[N], b[N], cnt=0, mo[N], ans=0;
queue<int> q;
bool topsort()
{
	for (int i=1; i<=n; i++)
		if (!d[i]) q.push(i);
	while (!q.empty())
	{
		int t=q.front();
		q.pop();
		b[++cnt]=t;
		
		for (int i=0; i<a[t].size(); i++)
		{
			int v=a[t][i];
			d[v]--;
			if (!d[v]) q.push(v);
		}
	}
	
	if (cnt<n) return false;
	return true;
}
int main()
{
	scanf("%d%d", &n, &m);
	for (int i=1; i<=m; i++)
	{
		scanf("%d%d", &u1, &v1);
		a[u1].push_back(v1);
		d[v1]++;
	}
	
	if (!topsort())
	{
		printf("Poor Xed");
		return 0;
	}
	for (int i=1; i<=cnt; i++) mo[i]=100;
	for (int i=cnt; i>=1; i--)
	{
		int u=b[i];
		for (int j=0; j<a[u].size(); j++)
		{
			int v=a[u][j];
			mo[u]=max(mo[u], mo[v]+1);
		}
	}
	for (int i=1; i<=cnt; i++) ans+=mo[i];
	printf("%d", ans);
    return 0;
}