2023南海区区赛模拟（初中组）T3删除区间

第3题删除区间查看测评数据信息

开始给你N个元素的数组（下标从1开始），数组里的数是1,2,3,…,N，然后执行D次删除操作。每次删除操作给一个区间[lo, hi]，要求删除下标位置从lo到hi的数，数组里的数据个数会减少hi-lo+1个。

例如，N=8，第1次删除操作区间是[3 4]，结果为”1,2,5,6,7,8”；第2次删除操作区间是[4 5]，结果为”1,2,5,8”。

最后，输出第M位的数字是什么。如果剩余的数不够M个，输出-1。

输入格式

(多组数据形式)

第1行：一个不超过10 的正整数K，表示有K组任务。

下面有K组数据，每组数据格式为：

第一行有3个正整数：N M D 。N范围为[1, 2000000000]，M范围为[1, N]，D范围为[1, 50]。

下面有D行，每行是用”-“连接（没有空格）的2个整数: lo-hi。保证1 ≤ lo ≤ hi ≤ n。

输出格式

输出第M位的数字，或-1。

输入/输出例子1

输入：

8 3 2

3-4

4-5

100 13 3

19-50

19-19

100 39 3

19-50

19-19

输出：

-1

样例解释

无

先考虑暴力，10分

#include <bits/stdc++.h>
using namespace std;
 
int t, d, x, y, n, m;
map<int, int> a;
int main()
{
    scanf("%d", &t);
    while (t--)
    {
        int k=0, flag=0;
        scanf("%d %d %d", &n, &m, &d);
        for (int i=1; i<=n; i++) a[i]=i;
 
        for (int i=1; i<=d; i++)
        {
            scanf("%d-%d", &x, &y);
            for (int j=1; j<=n; j++)
            {
                if (a[j]!=0) k++;
                if (k>=x && k<=y) a[j]=0;
                if (k>y) break;
            }
            k=0;
            /*for (int i=1; i<=n; i++)
                cout<<a[i]<<' ';
            cout<<endl;*/
        }
         
        for (int i=1; i<=n; i++)
        {
            if (a[i]!=0) k++;
            if (k==m)
            {
                flag=1;
                printf("%d\n", i);
                break;
            }
        }   
        if (flag==0) printf("-1\n");
    }
    return 0;
}

　　分析：这道题其实毕竟有意思，可以逆推，也可以模拟

模拟和上一题差不多（可能？）分裂区间

设有[1,8]区间，删除[3,4]，分裂成2个区间，变成125678，也就是[1,2]、[5,8]

再删除[4,5]，分裂成3个区间，[1,2]不变，125678，变成1278，也就是[1,2][5,5][8,8]

再删除[1,3]，变成[8,8]这个区间

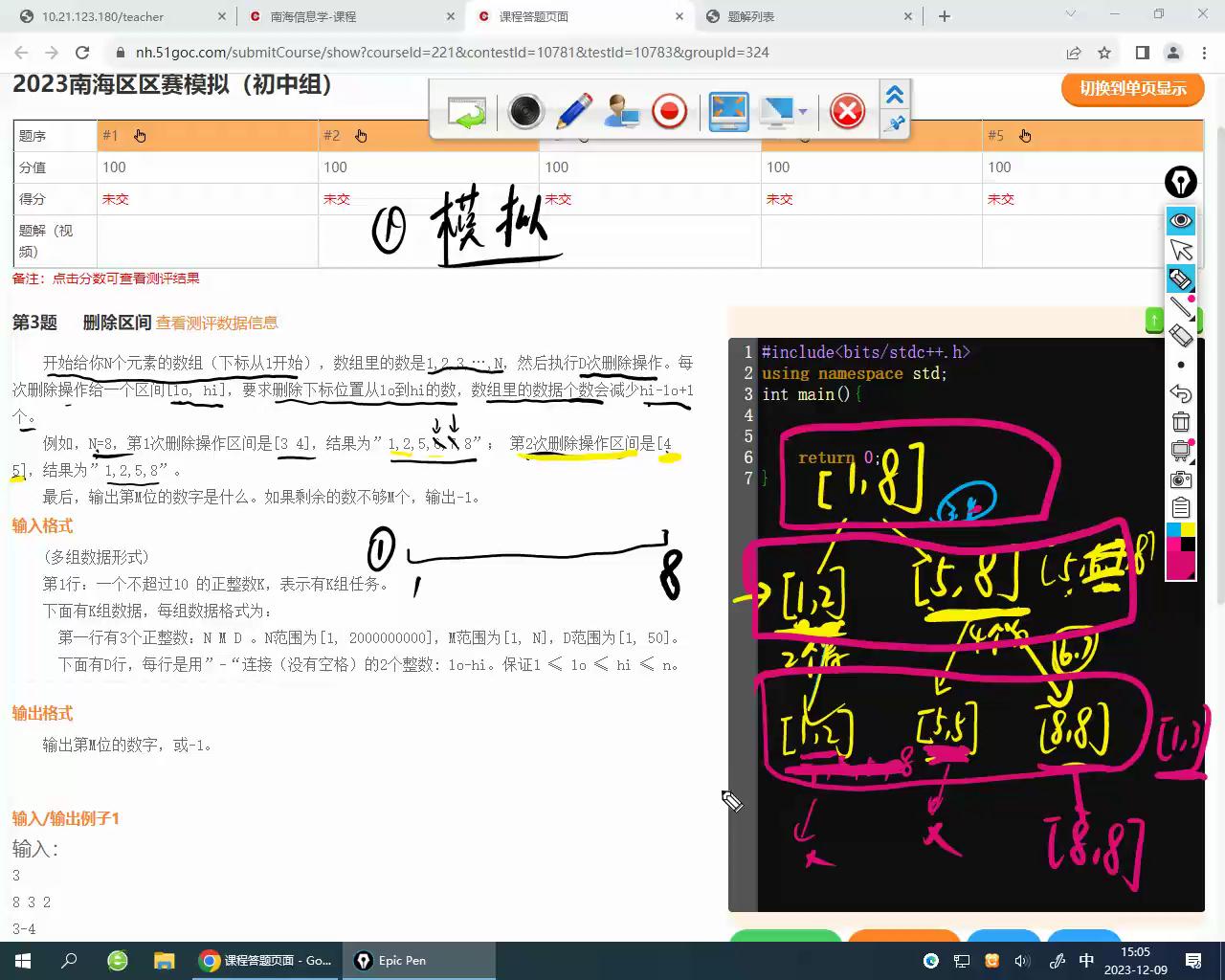
我们分析一下，红色笔圈出的区间为删除区间，发现每次区间数量变化只可能+1，-1，+0

带入具体数字，有区间[1,100][150,200][300,500]，删除[51,150]，如下

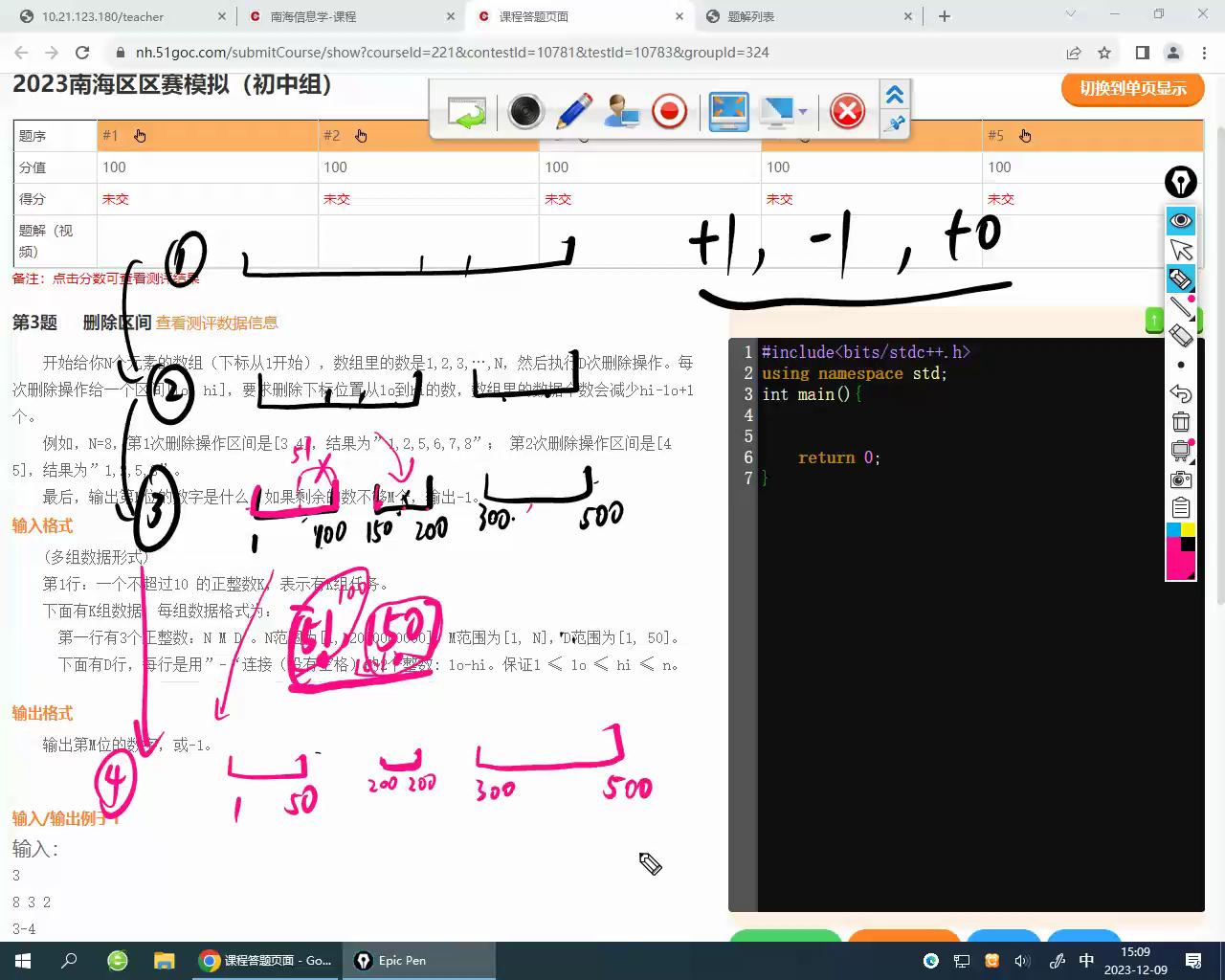
再删[49,52]

这就是分裂过程了，正为模拟，那么反着呢，为倒推

图解：

我们可以设有区间[1,7]删除[1,3]、[2,3]区间，求第二个数

正推很容易，但是不好写（我个人觉得），考虑逆推

因为最后要我们求第2个数，假设最后有一堆数（1-7），然后第2个数为2，删除的区间是2,3，我们删除2,3后，第二个数为4，然后跟着4往上，删除1,3，第二个数为7

因为我们相求第2个数，所以就要“跟踪”，从后面往前面推，想知道第二个数，就得知道4，想知道4在上一次操作的第几个数，就得继续往上推

例子2：

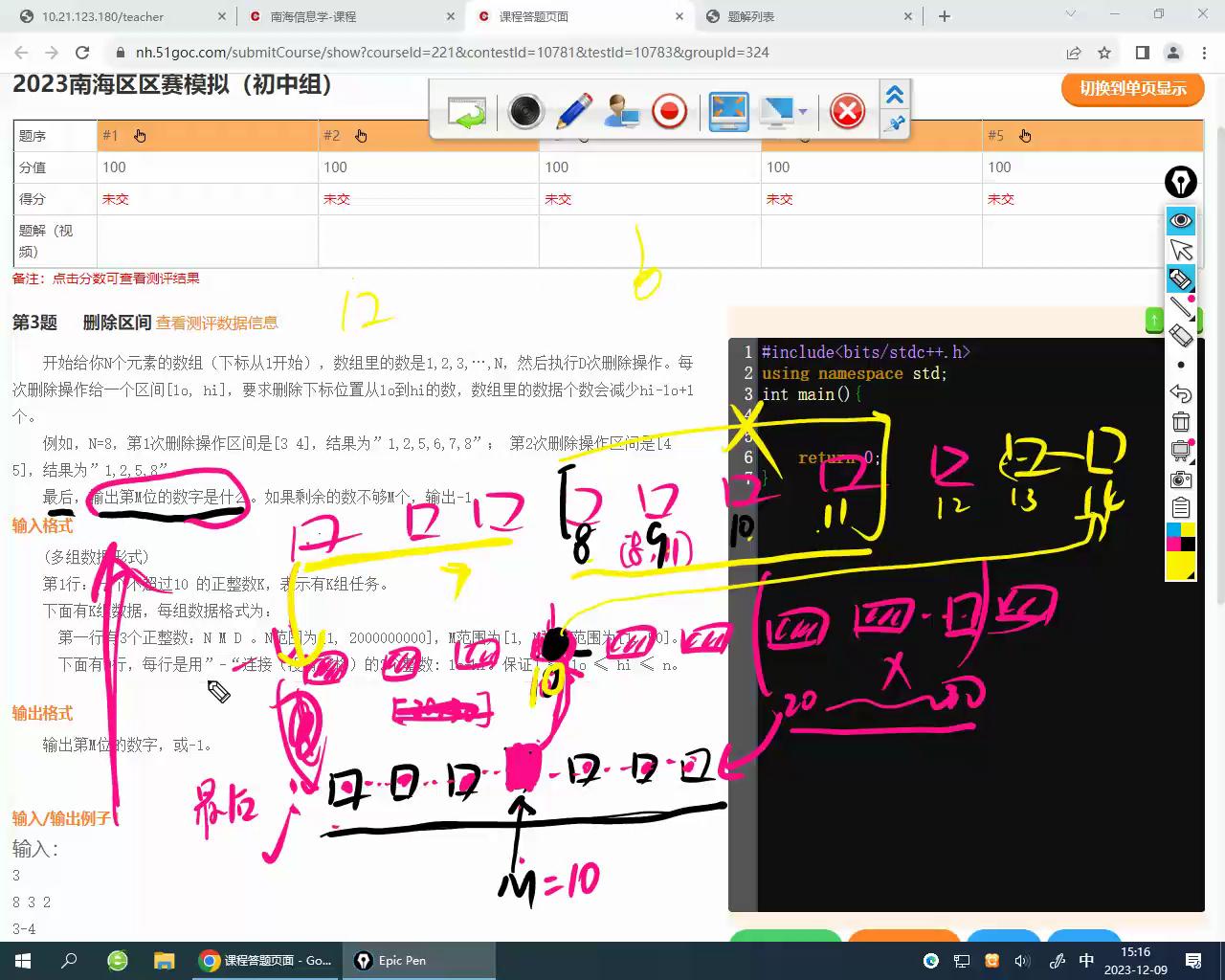
这就是2个分析了

__EOF__

本文作者：cnsdsg886-帥
本文链接：https://www.cnblogs.com/didiao233/p/17891355.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！