梯度下降求解非线性方程组

求解此方程组

 

参考资料

梯度下降求解非线性方程组 - 简书 (jianshu.com)

Gradient descent - Wikipedia

 

 

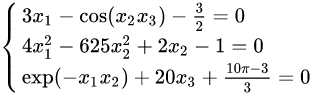
代码

import numpy as np
import matplotlib.pyplot as plt


def G(x1, x2, x3):
    tmp1 = 3*x1-np.cos(x2*x3)-3/2
    tmp2 = 4*x1**2-625*x2**2+2*x2-1
    tmp3 = np.exp(-x1*x2)+20*x3+(10*np.pi-3)/3

    return np.array([[tmp1],
                     [tmp2],
                     [tmp3]]).reshape(3, -1)


def JG(x1, x2, x3):
    '''
    梯度

    '''
    JG = np.array([[3, np.sin(x1*x2)*x3, np.sin(x2*x3)*x2],
                  [8*x1, -1250*x2+2, 0],
                  [-x2*np.exp(x1*x2), -x1*np.exp(x1*x2), 20]])
    return JG


def F(x1, x2, x3):
    tmp1 = 3*x1-np.cos(x2*x3)-3/2
    tmp2 = 4*x1**2-625*x2**2+2*x2-1
    tmp3 = np.exp(-x1*x2)+20*x3+(10*np.pi-3)/3
    return (1/2)*(tmp1**2+tmp2**2+tmp3**2)


def DeltaF(x1, x2, x3):
    return np.matmul(JG(x1, x2, x3).transpose(), G(x1, x2, x3))


alpha = 0.0001

X1 = x1_0 = 0
X2 = x2_0 = 0
X3 = x3_0 = 0

# 保存梯度下降经过的点
globalX1 = [x1_0]
globalX2 = [x2_0]
globalX3 = [x3_0]
globalF = [F(x1_0, x2_0, x3_0)]

epoch = 0
tempResult = 10
tempResultLis = []
while True:
    temp = np.array([[X1], [X2], [X3]]) - alpha*DeltaF(X1, X2, X3)
    X1, X2, X3 = temp[0][0], temp[1][0], temp[2][0]

    # 重新赋值
    temX1, temX2, temX3 = X1, X2, X3
    globalX1.append(temX1)
    globalX2.append(temX2)
    globalX3.append(temX3)

    if abs((F(X1, X2, X3)-tempResult)) < 0.0001 or epoch == 1000:
        print('epoch=', epoch)
        break

    epoch += 1
    tempResult = F(X1, X2, X3)
    tempResultLis.append(tempResult)

X = np.arange(len(tempResultLis))
plt.plot(X, tempResultLis)
plt.show()
print(u"最终结果为:(x1,x2,x3,G)=(%.5f, %.5f, %.5f, %.5f)" %
      (X1, X2, X3, F(X1, X2, X3)))