算法复杂度分析

数据结构和算法

• 基本概念

  数据结构指存储数据的结构,算法指的是操作数据的方法.数据结构是算法是相辅相成的,算法需要作用到特定的数据结构.

• 常用数据结构

  数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树

• 常用算法:

  递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规 划、字符串匹配算法

算法复杂度分析

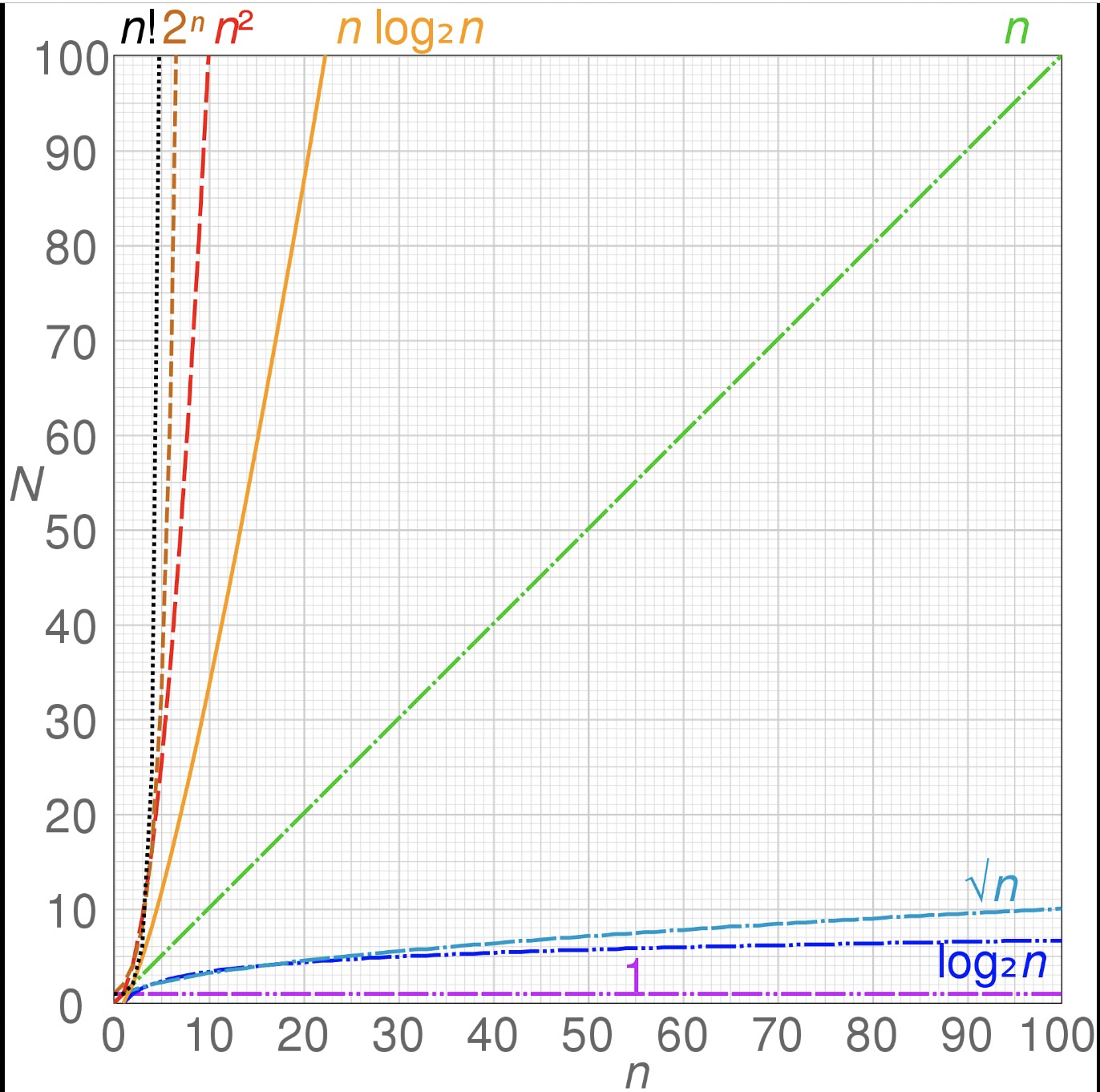
由于相同算法在不同测试环境,硬件设备上处理数据的效率并不相同,且不同算法的执行效率受数据规模的影响很大(如下图).所以在实际编码和进行算法优时就需要有一个理论分析方向作为指导.算法复杂度分析使用大O复杂度分析法.

 

时间复杂度

也叫时间渐进复杂度，并不表示准确的代码运行时间,而是表示代码执行时间随着数据规模增长的变化趋势,以下为维基百科关于时间复杂度的解释:

在计算机科学中，算法的时间复杂度（Time complexity）是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。例如，如果一个算法对于任何大小为 n （必须比 n0 大）的输入，它至多需要 5n3 + 3n 的时间运行完毕，那么它的渐近时间复杂度是 O(n3).

func TestNN(n int) int {
	var sum int
    for i:=0;i<n;i++{
        for j:=0;j<n;j++{
            sum+=i*j
        }
    }
    return sum
}

func TestN(n int) int {
	var sum int
    for i:=0;i<n;i++{
        sum+=i
    }
    return sum
}

func Test1(n int) int {
    return n
}

假设每一行代码 执行消耗cpu时间均为cpu_time, n表示数据规模,则以上三段代码逐行执行总时间为:

TNN(n)=(1+n+2n²+1)*cpu_time

TN(n)=(1+2n+1)*cpu_time

T1(n)=(1)*cpu_time

由上面表达式可以知道代码执行总时间 T(n) 与每行代码的执行次数 n 成正比,引入大O时间复杂度后,可以表示为:T(n)=O(f(n)),其中T(n)表示代码执行的时间;n 表示数据规模的大小;f(n) 表示每行代码执行的次数总和.

则代码执行时间TNN(n)=O(2n²+n+2);TN(n)=O(2n+2);T1(n)=O(1)

当 n 很大时,而公式中的低阶项、常数项(无论是100,1000,10000,100000……)、系数三部分并不能对增长趋势造成很大的影响,所以都可以忽略。 则上述3段代码的时间复杂度，就可以记为:TNN(n) = O(n²);TN(n) = O(n);T1=O(1)

时间复杂度分析方法

• 假设数据规模非常大

• 关注循环最多的那部分代码

• 总复杂度等于量级最大的那段代码的复杂度

• 嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

常见时间复杂度量级以及示例

• O(1)

func T1() int {
    i,j:=1,2
    return i+j
}

• O(logn)

func TLogN(n int) int {
    i:=1
    for i<n{
        i=3*n
    }
    return i
}
// 计算循环多少次, 3x次方=n 则x=log3 n,使用换底公式为 log3 2 * log2 n
// 由于log3 2是一个常量,则当n越来愈大时不影响代码执行时间趋势

• O(n)

func TN(n int) int {
    var sum int
    for i:=0;i<n;i++ {
        sum+=i
    }
    return sum
}

// 循环了n次

• O(nlog n)

func TNLonN(n int) int {
    var sum int
    for i:=0;i<n;i++ {
        sum+=i
        TLogN(n)
    }
    return sum
}

// O(n)*O(log n)=O(nlog n)

• O(n²)

func TN3(n int) int{
    var sum
    for i:=0;i<n;i++{
        for j:=0;j<n;j++{
        	sum+=i*j
    	}
    }
    return 
}
// O(n)*O(n)*O(n)=O(n³)

空间复杂度

也叫渐进空间复杂度，概念和时间复杂度类似，表示数据规模和存储空间的增长关系

举个例子:

func SpaceN(n int) {
    sli:=make([]string, n)
    for i:=0; i<n; i++ {
        sli[i] = "sli_" + string(i)
    }
}

上述代码第2行代码申请了容量为n的一个[]string 类型切片的存储空间，其他行代码申请的空间都是常量,所以空间复杂度为O(n)

 四个算法复杂度的概念

因为同一段代码，在不同输入的情况下，复杂度量级有可能是不一样,所以可以引入一下几种时间复杂度相关概念.

• 最好情况时间复杂度(best case timecomplexity)

  极端好的情况下算法时间复杂度

• 最坏情况时间复杂度((worst case timecomplexity)

  极端坏的情况下算法时间复杂度

• 平均情况时间复杂度(average case timecomplexity)

  随机情况下算法时间复杂度

• 均摊时间复杂度(amortized time complexity)

  存在时序规律的平均情况时间复杂度

// 从给出的切片中找出与t相等的元素的位置
// 切片长度为n
func find([]int sli, int t) int {
    for index,s := range sli {
        if (sli[index] == t){
            return index
        }
	}
	return -1;
}

从时间复杂度角度分析上述代码,时间复杂度为O(n),n=len(sli).

有个问题是切片中元素位置随机，当与t相等的元素的位置为0时，那么查找1次的时候就被找到,那么程序结束时实际时间复杂度为O(1);当与t相等的元素的位置为n-1时,那么需要查找n次才被找到,那么程序结束时实际时间复杂度为O(n)。这种情况下使用时间复杂度O(n)显然无法相对准确表示该代码的执行用时，所以引入最好情况时间复杂度，最坏情况时间复杂度，平均情况时间复杂度3个概念。

以上述代码为例，最好情况时间复杂度为O(1), 最坏情况时间复杂度为O(n)。

那么平均情况复杂度呢, 假设t在数组里和不在数组里概率均为1/2，则t取值sli[0]至sli[n-1]的概率均为1/2n,所以代码执行次数为1x1/2n+2x1/2n+3x1/2n+4x1/2n+...+nx1/2n=(3n+1)/4,所以最终平均情况复杂度也为O(n)

const N = 1000
var arr = [N]int{}
var count = 0
func Insert(t int) {
	if count > n-1 {
        // 对arr进行软清空
		count = 0
		sum := 0
		for _, a := range arr {
			sum += a
		}
        // 把sum放到arr第一个位置
		arr[count] = sum
		count++
	}
	arr[count] = t
	count++
}

上述代码定义一个数组[N]int类型的arr,然后Insert方法实现插入操作，每插入N个数据,就需要进行一次累加，并将累加结果放到arr[0]一次类推。

Insert函数当arr有剩余空间时的复杂度在最好情况下是O(1)，当arr没有空余空间时最坏情况是O(N)

非最好情况下和最坏情况下(实际情况)时，代码执行次数(加权平均) N+N/(N+1)=2N/(N+1)所以实际复杂度为O(1)

Insert跟find函数相比比较明显的区别是find除了最好和最坏情况完全是随机的，而insert在最好和最坏之外海有一定规律，在每一次复杂度为O(n)的操作后，都跟着N-1次复杂度为O(1)，然后依次反复。

这种情况下引入均摊时间复杂度来表示时间复杂度，即把O(n)的复杂度均摊到后面的n-1次O(1)上，可以理解为只是常量系数的变化，而量级并没有发生变化，所以复杂度还是O(1).