第十三届重庆市程序设计大赛
第十三届重庆市程序设计大赛
https://codeforces.com/gym/105887
F:
题目大意:

void solve(){
int a,b,c;
cin>>a>>b>>c;
if (a>b) cout<<"Win"<<endl;
else if (c>b) cout<<"WIN"<<endl;
else cout<<"nowin"<<endl;
}
签到
L:
题目大意:

const LL mod=998244353;
void solve(){
int n;
cin>>n;
LL sum=0;
vector<LL> v;
for (int i=1;i<=n;i++){
string s;
cin>>s;
if (s=="Push"){
LL x;
cin>>x;
v.push_back(x);
sum=(sum+x)%mod;
cout<<sum<<endl;
}else if (s=="Pop"){
sum=(sum-v.back()+mod)%mod;
v.pop_back();
cout<<sum<<endl;
}else{
sum=(sum*2)%mod;
if (v.size()<200010){
int n=v.size();
for (int i=0;i<n;i++) v.push_back(v[i]);
}
cout<<sum<<endl;
}
}
}
模拟一次就行,对当前栈做 Repeat 操作,栈内元素和翻倍,对放入和弹出操作单独处理贡献,防止模数为负
并且弹出 Pop 操作最多执行 \(2e5\) 次,那么当栈内元素大于 \(2e5\) 时可以忽略 Repeat 操作,否则就利用数组依次复制栈内元素
均摊时间复杂度为 \(O(m+2e5)\)
A:
题目大意:

int a[100010];
void solve(){
int n;
cin>>n;
for (int i=0;i<n;i++) cin>>a[i];
bool f=1;
int d=a[0];
for (int i=0;i<n;i++)
if (d!=a[i]) f=0;
if (f==1){cout<<0<<endl; return;}
for (int i=1;i<=sqrt(n);i++){
int d=a[0]|a[i];
bool f=1;
for (int j=0;j<n;j++){
a[j]|=a[(j+i)%n];
if (d!=a[j]) f=0;
}
if (f==1){cout<<i<<endl; return;}
}
}
将 \(or\) 操作视作二进制位 \(1\) 在二进制位 \(0\) 上的传播,每轮传播的步长为 \(T\) ,具体的说:
\(a_{i,j}\) 表示 \(a_i\) 用二进制表示下的第 \(j\) 位,当 \(a_{i,j}\) 为 \(1\) 时,第 \(T\) 轮 \(a_{(i+T)\%n,j}\) 被传播到 \(1\)
最终的数组所有元素一定会归敛到一个确定的值,即所有的 \(a_{i}=A\),每一轮传播都表示将 \(a_{(i+T)\%n}\) 元素附加上 \(a_{i}\) 的性质
假设只存在一个数 \(a_i=1\) ,其余都是 \(0\) ,每次传播后,都有 \(1,1,2,3\cdots T\) 个数被附加上 \(1\)
估计时间复杂度为 \(o(n\sqrt n)\) ,所以枚举两层即可
H:
题目大意:

void solve(){
int n;
cin>>n;
int idx=0;
unordered_map<int,int> mp;
vector<int> a(n+1),b=a;
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++) cin>>b[i];
for (int i=1;i<=n;i++) mp[b[i]]=++idx;
vector<int> v;
for (int i=1;i<=n;i++){
int f;
cin>>f;
if (f==1)
v.push_back(mp[a[i]]);
}
if (v.size()==0){cout<<"Yes"<<endl; return ;}
int d=v.front();
for (auto it:v){
if (d>it){cout<<"No"<<endl; return;
}else
d=it;
}
cout<<"Yes"<<endl;
}
可以发现出现交叉的情况下无解,并且能出现交叉当且仅当上面紧贴边界的小球与下面紧贴边界的小球出现交叉
即需要判断上面紧贴的小球对应下面紧贴边界的小球之间的相对位置是否改变
可以将下面紧贴的小球的编号重新映射一个编号,然后用映射后的值判断上面紧贴的小球是否存在逆序
如果存在逆序,则将小球连接后会出现交叉
不紧贴上边界的小球对整体不产生影响,因为连接下面的小球与不紧贴上边界的小球后,整块操作区域并不会被分割,其余所有的连接线都能够绕过这一条连接线
C:
题目大意:

int g[1010][1010];
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++) g[1][i]=i;
for (int i=2;i<=n;i++) g[i][1]=(g[i-1][1]+i-1)%n+1;
for (int i=2;i<=n;i++){
for (int j=2;j<=n;j++){
g[i][j]=(g[i][j-1])%n+1;
}
}
for (int i=1;i<=n;i++){
for (int j=1;j<=n;j++){
cout<<g[i][j]<<' ';
}
cout<<endl;
}
}
构造题,为了使着色数最大,且相邻的不同区域的格子颜色不同
那么使每一个区域的格子都与其余区域的格子相邻,那么着色数最大为 \(n\)
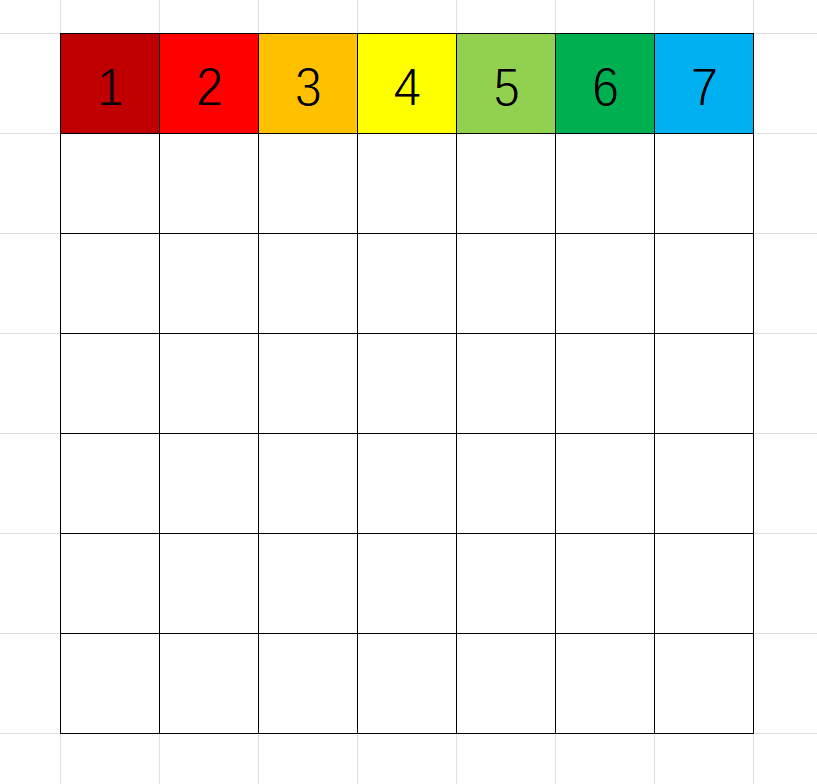
先构造第一行,从 \(1\) 开始依次排开,为了使所有的区域与其他区域都相邻,那么第二行的 \((2,i)\) 与 \((1,i)\) 要在第一行没有相邻
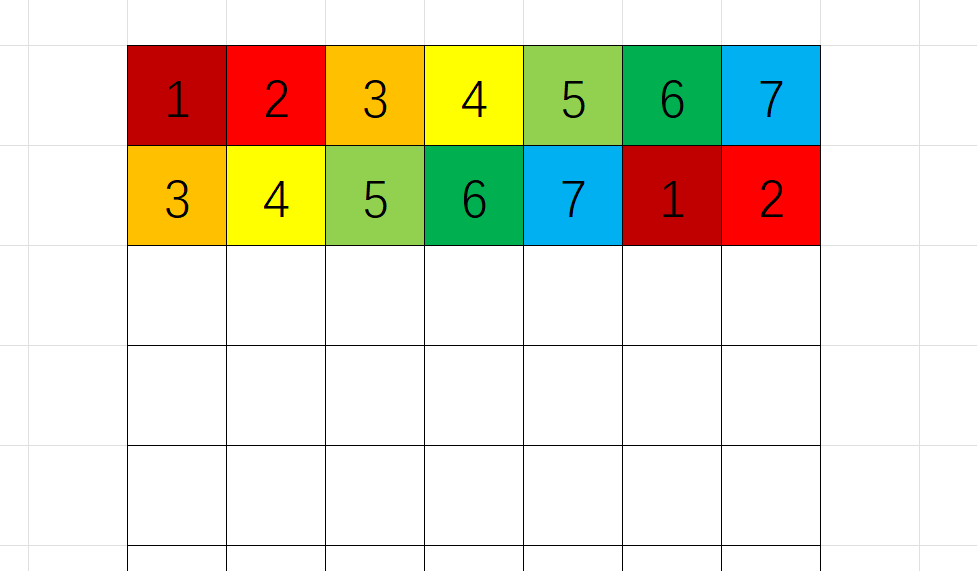
所以让 \(3\) 在 \(1\) 的下方,这样构造出来当前相邻数最优方案,同理有第三行
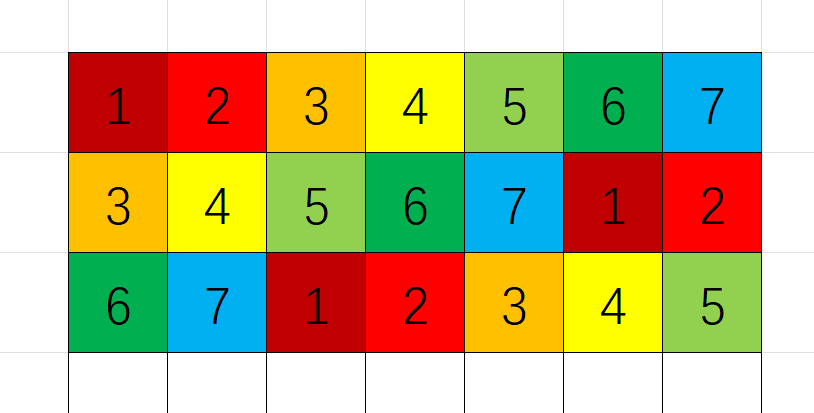
让 \(6\) 在 \(3\) 的下方,因为之前不存在 \(3,6\) 相邻的情况
可以概括出第一列的构造公式 \(g_{i,1}=g_{i-1,1}+i-1\) 即每一行的第一个元素两两之差形成等差公式
行内元素依次排开即可,循环取模
B:
题目大意:

LL d[200010];
LL p[200010];
void solve(){
memset(d,0,sizeof d);
memset(p,0,sizeof p);
int n,m;
cin>>n>>m;
vector<LL> l(m+1),r(m+1),c(m+1);
set<LL> st;
for (int i=1;i<=m;i++){
cin>>l[i]>>r[i]>>c[i];
st.insert(l[i]);
st.insert(r[i]);
}
unordered_map<LL,int> mp;
int idx=0;
if (!st.count(n)||!st.count(1)){cout<<0<<endl; return;}
for (auto it:st) mp[it]=++idx;
for (int i=1;i<=m;i++){
d[mp[l[i]]]+=c[i];
d[mp[r[i]]]-=c[i];
}
LL ans=2e18;
for (int i=1;i<=idx-1;i++){
p[i]=p[i-1]+d[i];
ans=min(ans,p[i]);
}
cout<<ans<<endl;
}
离散化+差分,将每段区间视为一条线段
原问题相当于对一段区间 \([l,r]\) 进行区间修改,每一站的最大乘车人数相当于覆盖这个点的线段的权值和
因为第 \(i\) 个站的乘车人数一定不大于第 \(i-1\) 个站的乘车人数,所以在维护出每个点的最大乘车人数后从 \(1\) 开始向后连续取 \(min\)
第 \(n-1\) 个站的最大乘车人数即为答案,特别的考虑起点和终点不覆盖 \(1,n\) 的特殊情况
直接利用 map 进行顺序离散化的简单写法:
void solve(){
int n,m;
cin>>n>>m;
map<int,LL> mp;
for (int i=1;i<=m;i++){
int l,r,c;
cin>>l>>r>>c;
mp[l]+=c,mp[r]-=c;
}
if (mp.begin()->first>1||mp.rbegin()->first<n){
cout<<0<<endl;
return;
}
LL ans=2e18,sum=0;
for (auto it:mp){
sum+=it.second;
if (it.first<n) ans=min(ans,sum);
}
cout<<ans<<endl;
}
(STL中 begin() 指向容器的第一个元素,end() 指向最后一个元素的下一个元素,同样的有反向迭代器 rbegin(),rend())
J:
题目大意:

char c[200010];
vector<int> e[200010];
vector<int> dg(200010);
queue<int> q;
unordered_map<char,int> cnt;
int bfs(char color){
int sum=0;
bool vis[200010]={0};
vector<int> bk=dg;
while (q.size()){
auto t=q.front();
q.pop();
if (vis[t]) continue;
vis[t]=1;sum++;
for (auto v:e[t]){
bk[v]--;
if (vis[v]||c[v]!=color||bk[v]!=1) continue;
q.push(v);
}
}
return sum;
}
void solve(){
int n;
cin>>n;
for (int i=1;i<=n;i++){
cin>>c[i];
cnt[c[i]]++;
}
for (int i=1;i<n;i++){
int u,v;
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
dg[u]++;dg[v]++;
}
int ans=0;
char tmp[]={'R','G','B'};
for (int d=0;d<3;d++){
for (int i=1;i<=n;i++)
if (dg[i]==1&&c[i]==tmp[d])
q.push(i);
ans+=cnt[tmp[d]]-bfs(tmp[d]);
}
cout<<ans<<endl;
}
考虑对一种颜色,例如所有节点对 \((u,v)\) ,若 \(u,v\) 颜色均不为 \(R\) ,则两节点简单路径上也不存在 \(R\) 节点
则在任意两个节点 \(u,v\) 之间一定不存在 \(R\) 节点,相当于需要把这两个节点间所有的 \(R\) 节点染为白色
当 \(u,v\) 中某个节点为 \(R\) 时,这一对节点对答案没有贡献,因为不满足 \(u,v\) 颜色均不为 \(R\) 的前提
那么当节点 \(u\) 为 \(R\) 时且 \(u\) 为叶子节点,则可将 \(u\) 删去,不影响答案(节点 \(v\) 的所有儿子被删去后,那么 \(v\) 也变为叶子节点)
题意便转化为对一种颜色 \(color\) ,删去树上所有为 \(color\) 的叶子节点后,剩余连通块上 \(color\) 的节点个数
且三种颜色对答案的贡献是独立的,所以分开计算结果即可
int ans=0;
char tmp[]={'R','G','B'};
for (int d=0;d<3;d++){
for (int i=1;i<=n;i++)
if (dg[i]==1&&c[i]==tmp[d])
q.push(i);//将所有为color的叶子节点放进队列中
ans+=cnt[tmp[d]]-bfs(tmp[d]);//贡献为这个颜色的全部个数减去可删去的节点数
}
int bfs(char color){
int sum=0;
bool vis[200010]={0};
vector<int> bk=dg;//拷贝度数
while (q.size()){
auto t=q.front();
q.pop();
if (vis[t]) continue;//所有节点只入队一次
vis[t]=1;sum++;//计算被删去的节点个数
for (auto v:e[t]){
bk[v]--;//删去节点t后,与他连接的所有节点度数减一
if (vis[v]||c[v]!=color||bk[v]!=1) continue;
q.push(v);//v的度数为1且颜色为color,那么v也可被删去
}
}
return sum;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号